1.工作原理

带的工作原理是靠摩擦传动。如图6-4所示：小带轮在电动机的驱动下顺时针旋转，带要阻碍带轮的运动，作用于带轮的摩擦力逆时针方向如图中轮ΣF_f；而带轮给带的摩擦力与带给轮的摩擦力互为作用力与反作用力，大小相等方向相反，为顺时针方向，即图中带ΣF_f，因此带在摩擦力的作用下以速度v顺时针旋转。带运动至进入大带轮时，大带轮要阻碍带的运动，作用于带的摩擦力方向与带的运动方向相反，即为逆时针，即图中带ΣF_f。同理，带给带轮的摩擦力为顺时针，如图中的轮ΣF_f。因此从动轮在摩擦力的驱动下顺时针旋转。

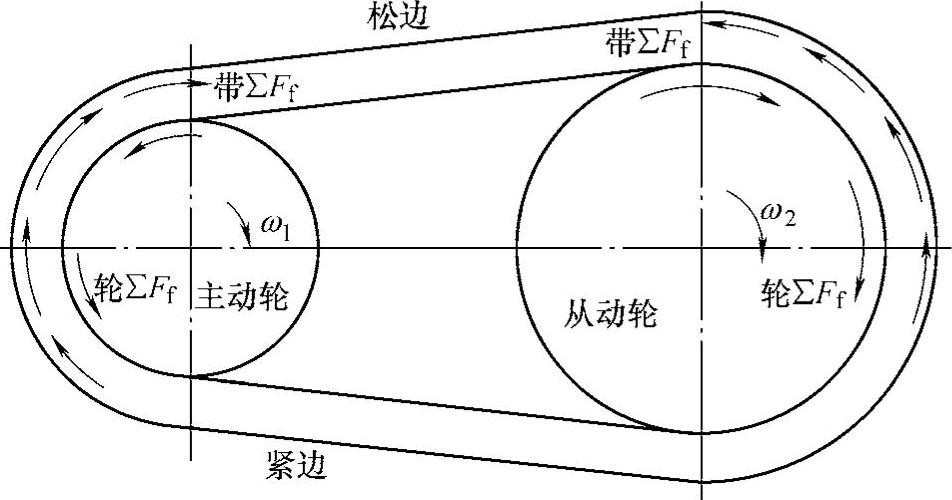
图6-4 带传动工作原理图

2.受力分析

带工作前两边拉力（即初拉力F₀）相等；工作时，由于带所受摩擦力的方向（见图6-4），使带下边的拉力由F₀增大至F₁，即紧边拉力，另一边（上边）的拉力由F₀减小至F₂为松边拉力，拉力差（F₁-F₂）即为有效拉力F，其数值等于沿带轮接触弧上摩擦力之总和，即

F=F₁-F₂=ΣF_f （6-1）

若带的总长不变，紧边拉力的增量应等于松边拉力的减量，即

F₁-F₂=F₀-F₂

故 F₁+F₂=2F₀ （6-2）

带在即将打滑、但还没打滑时紧边拉力与松边拉力之比的关系应符合弹性体的欧拉公式，即

如果考虑离心力则式（6-3）变为

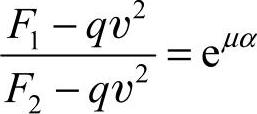
联立式（6-1）、式（6-3）可得紧边拉力F₁、松边拉力F₂和有效拉力F之间的关系式：

式中 e——自然对数的底（e=2.7182…）；

μ——带和带轮之间的摩擦系数（对V带传动用当量摩擦系数μ_v）；

α——带在小带轮上的包角（rad）；

q——每米带长的质量（kg/m）；

v——带速（m/s）。

式（6-6）是另一种形式的欧拉公式，在推导设计式时会用到。

3.应力分析

带在工作时不仅受由拉力产生的拉应力，还受由离心力产生的拉应力和弯曲应力。

（1）由紧边和松边拉力产生的拉应力 紧边拉应力σ₁

σ₁=F₁/A （6-7）

松边拉应力σ₂

σ₂=F₂/A （6-8）

式中 A——传动带的横截面积（mm²）。

（2）由离心力产生的拉应力σ_c 当带在带轮上作圆周运动时，由于本身的质量将产生离心力，为平衡离心力在带内引起离心力，虽然离心力只产生在带作圆周运动的部分，但由于带是一个整体，所以由此产生的离心拉力F_c作用在带的全长上，其大小按下式计算。

F_c=qv² （6-9）

式中 q——传动带每米长的质量（kg/m）；

v——带速（m/s）。

故

σ_c=F_c/A=qv²/A （6-10）

（3）绕过带轮处弯曲应力σ_b

(www.daowen.com)

式中 E——材料的弹性模量（MPa）；

y——带的最外层到节线的距离（mm）；

d——带轮基准直径（mm）。

最大应力发生在紧边绕入小带轮之处，其值为紧边拉应力、离心拉应力与小带轮的弯曲应力之和，即

σ=σ₁+σ_c+σ_b1 （6-12）

带的应力分布图及最大应力点如图6-5所示。由于交变应力的作用，将引起带的疲劳破坏而失效，表现为脱层、撕裂、拉断，限制了带的使用寿命。

4.弹性滑动和打滑

（1）弹性滑动

1）弹性滑动的概念及后果。由于带是弹性体，受力不同时，带的变形量也不相同。在主动轮上，当带从紧边a点转到松边b点时，拉力由F₁逐渐降至F₂，带因弹性变形渐小而回缩，带的运动滞后于带轮，如图6-6所示。也就是说，带与带轮之间产生了相对滑动。同样发生在从动轮上，但带的运动超前于带轮。这种由于带的弹性变形而引起的带与带轮之间的相对滑动，称为弹性滑动，又称丢转。弹性滑动是带传动的固有特性，不可避免。

弹性滑动将引起下列后果：①从动轮的圆周速度低于主动轮的圆周速度；②降低了传动效率；③引起带的磨损；④使带的温度升高。

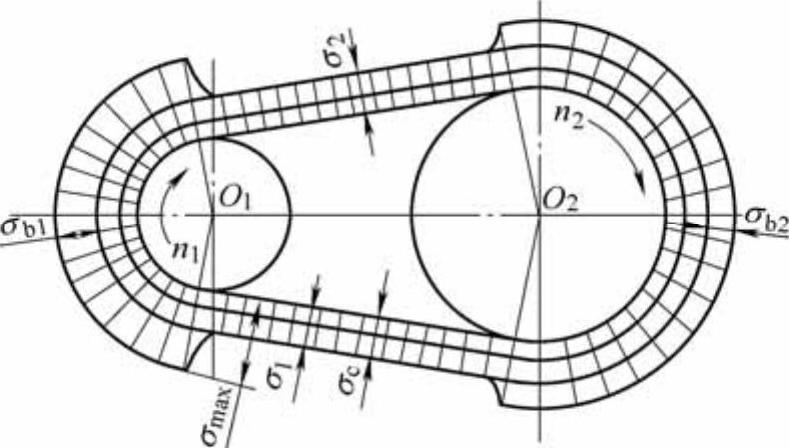
图6-5 带传动应力分布图

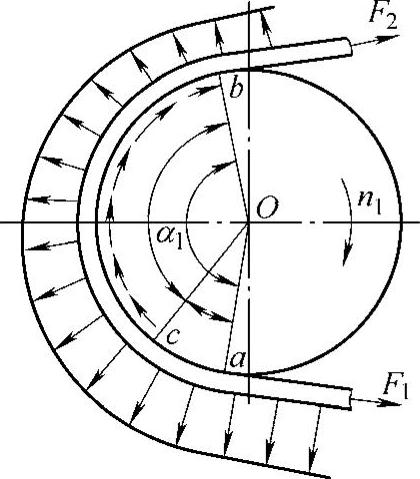
图6-6 带的弹性滑动

2）弹性滑动率。由弹性滑动引起从动轮轮缘圆周速度，相对于主动轮轮缘圆周速度的减小率称为滑动率（或滑动系数），用ε表示，可以表示为

传动比

从动轮转速

n₂=（1-ε）n₁d₁/d₂ （6-15）

带传动的滑动率ε通常为0.01～0.02，在一般计算中可忽略不计，故

i≈d₂/d₁ （6-16）

（2）打滑 当带传递载荷超过极限摩擦力时，带的弹性滑动普及全部接触弧，称为打滑。这是由于超载引起的，是应该避免的。

5.失效形式和设计准则

（1）带传动的失效形式

1）打滑。过载造成带与轮的全面滑动，一旦打滑，带传动失效，带剧烈磨损。

2）带的疲劳破坏。由于交变应力的作用，当最大应力σ_max=σ₁+σ_c+σ_b1超过皮带的许用应力[σ]时，将引起带的疲劳破坏而失效，表现为脱层、撕裂、拉断，限制了带的使用寿命。

（2）设计准则 带传动的设计准则是在保证带传动不打滑的前提下，带具有一定的疲劳强度和寿命。

1）带的疲劳强度条件。由式（6-12）可知，带的最大应力σ_max=σ₁+σ_c+σ_b1 ，满足带不被疲劳拉断的强度条件为

σ_max=σ₁+σ_c+σ_b1≤[σ] （6-17）或

σ₁≤[σ]-σ_c-σ_b1 式中[σ]——在特定条件下由带的疲劳强度决定的许用应力（MPa）。

2）带在不打滑时的最大有效圆周力。带的最大有效圆周力F_max=F₁-F₂，与欧拉公式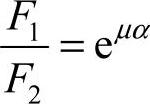联立得出带在不打滑时的最大有效圆周力为

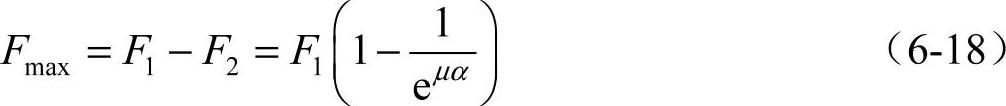
3）额定功率。带的设计准则应该是既不打滑又不发生疲劳断裂。要想不打滑就必须满足欧拉公式（6-6）；要想不发生疲劳断裂就必须满足带的疲劳强度条件即式（6-17）。以上两式联立即得出单根带能传递的力。但是实际应用中习惯用功率表示，因此带既不打滑且具有足够疲劳强度时单根带所能传递的功率P₀为

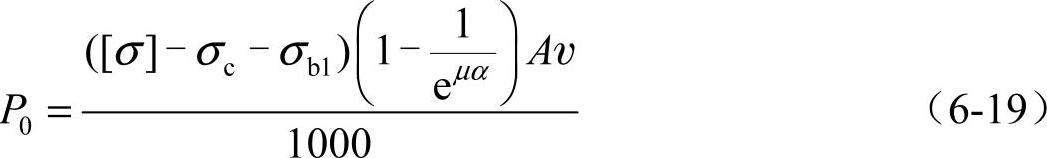
该式为计算各种摩擦带单根带所能传递功率的基本公式，再根据带的计算功率P_d除以单根带所能传递功率P₀，即得出带的根数，当然还要考虑一些系数等细节，见带的设计框图及设计实例。