工程中螺栓多为成组使用，单个使用极少，因此，须研究螺栓组的结构设计和受力分析，它是单个螺栓联接强度计算的基础和前提条件。

螺栓组联接设计的程序是选择布局、确定数目、受力分析、求出直径。

1.螺栓组联接的结构设计

螺栓组联接的结构设计原则如下。

1）螺栓布局要尽量对称分布，螺栓组中心与形心重合，对于圆形构件布置螺栓时，螺栓数目一定要取偶数，有利于分度、划线和钻孔。

2）每一组螺栓应设计成直径、长度、材料都相等，有利于加工且使产品更美观。

3）设计合理的螺栓间距，适当的边距，应满足扳手空间以利用板手装拆，尺寸可查机械设计手册。

4）装配时，对于紧螺栓联接，应使每个螺栓预紧程度（预紧力）尽量一致。

2.螺栓组联接的受力分析及结构设计

螺栓组联接受力分析的目的是求出一组受力最大的螺栓所受的力，为强度计算提供条件。为了简化计算，受力分析作如下假设。

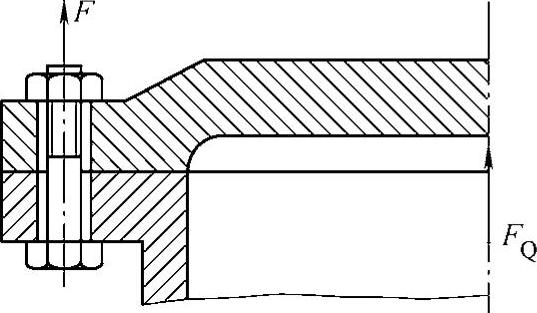
图5-9 螺栓组联接受轴向载荷

1）被联接件为刚性体。

2）各个螺栓的材料、直径、长度与F′相同。

3）螺栓的应变在弹性范围内。

根据以上假设，进一步讨论当作用于一组螺栓的外载荷是轴向力、横向力、转矩和翻倒力矩时一组螺栓中受力最大的螺栓所受的力。

（1）螺栓组联接受轴向载荷F_Q 如图5-9所示，作用于螺栓组几何型心的载荷为F_Q，每个螺栓受的工作拉力为

（2）螺栓组联接受横向载荷F_R 如图5-10所示，一组螺栓受横向载荷作用，螺栓是否受剪切取决于设计者采用哪一种结构的螺栓。如果采用受拉螺栓，则螺栓受拉而不受剪。

1）采用受拉螺栓（普通螺栓）。如图5-10a所示，此时的螺栓在安装时每个螺栓受预紧力F′作用，而被联接件受夹紧力（正压力）作用，夹紧力产生的摩擦力与外载荷平衡，即

F′zµ_Sm≥K_fF_R

2）采用受剪螺栓（铰制孔光制螺栓）。如图5-10b所示，此时外载荷直接作用在每个螺栓上，则每个螺栓所受的剪切力为

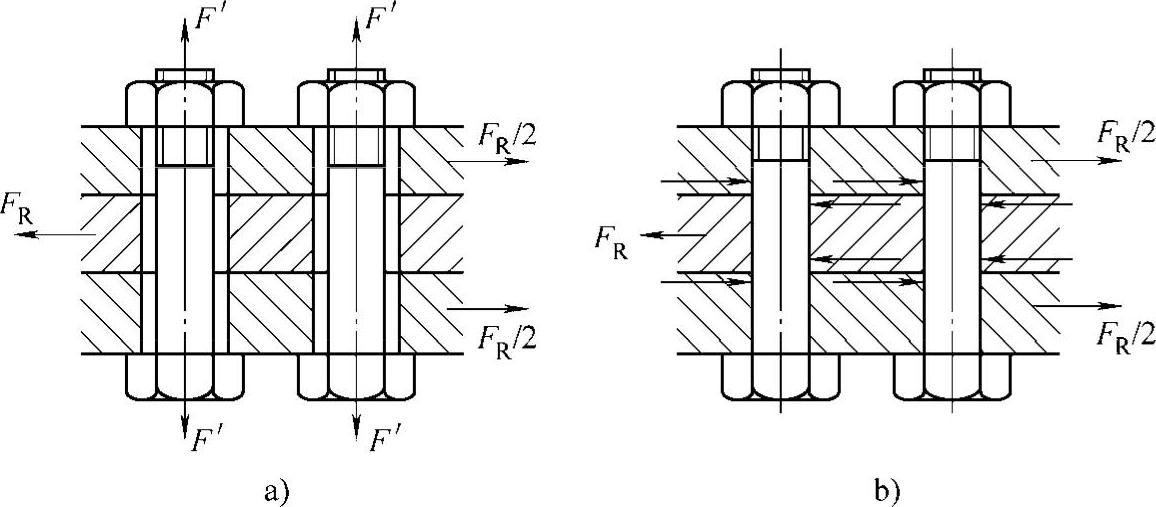
图5-10 螺栓组联接受横向载荷

（3）螺栓组联接受转矩T作用 如图5-11a所示，作用到一组螺栓几何型心的载荷是受转矩T，但对每个螺栓而言，就相当于受横向力作用，因此与前面分析的情况相同，也分两种情况考虑。

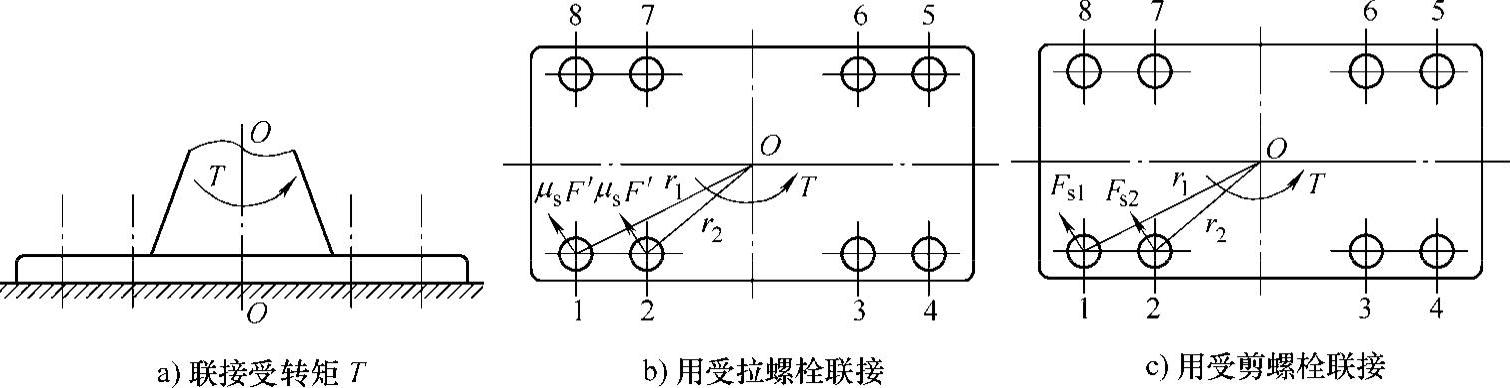
图5-11 螺栓组联接受转矩T作用(www.daowen.com)

1）设计成受拉螺栓（普通螺栓）。如图5-11b所示，此时靠摩擦传力，即转矩被底板的摩擦力矩平衡。分析底板受力为转矩T及各螺栓结合面摩擦力矩之和

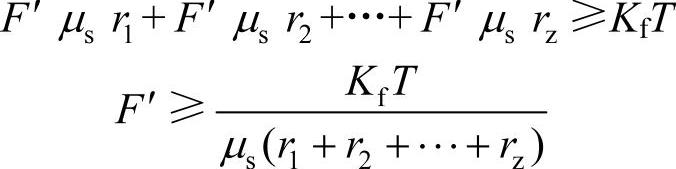
或写成

2）设计成受剪螺栓（铰制孔光制螺栓）。此时靠剪切传力，如图5-11c所示，底板受力为转矩T和螺栓给螺栓孔的反力矩，列出底板的受力平衡式得

T=F_s1r₁+F_s2r₂+…+F_szr_z （5-10）

但F_s1，F_s2，…，F_sz不知，且不等，可由变形协调条件求解。各螺栓剪切变形量与其中心到底板旋转中心距离成正比；又因螺栓材料、直径、长度相同，剪切刚度也相同，所以剪切力也与距离成正比（胡克定律），即

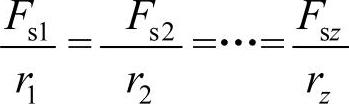
将F_s2，F_s3，…，F_sz都写成F_s1的函数，即

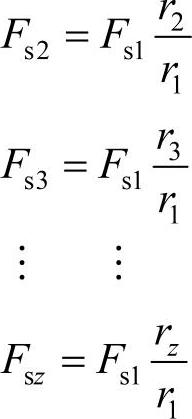
将以上各式代入式（5-10）得

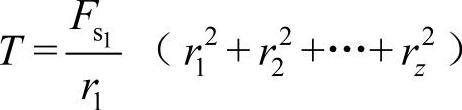
又因为F_s1=F_s4=F_s5=F_s8=F_max，因此也可写成通式，即一组螺栓中受力最大螺栓所受的力为

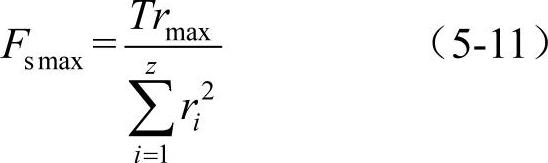
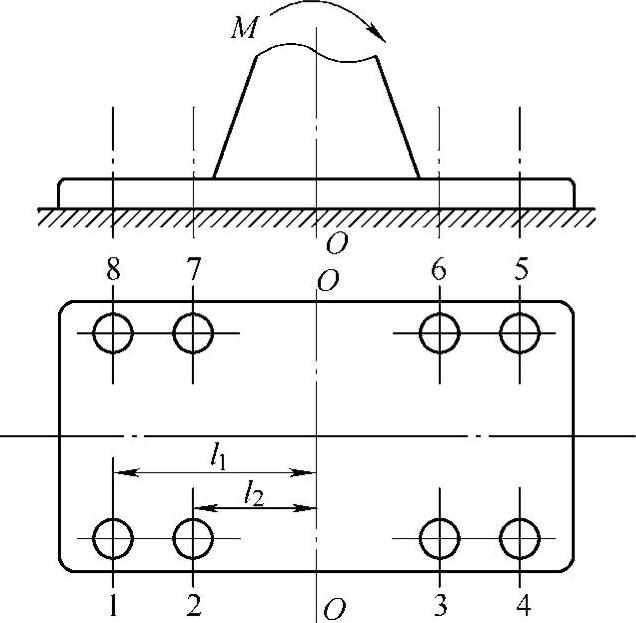
图5-12 螺栓组联接受翻倒力矩

（4）螺栓组联接受翻倒力矩M作用 如图5-12所示，此时，因为翻倒力矩M的方向与螺栓的轴线平行，因此螺栓只能受拉而不能受剪切。同时，为了接近实际并简化计算，又进行了重新假设：被联接件为弹性体，因此翻倒轴线为O—O而不是底板的右侧边。

底板受翻倒力矩M作用，还受左边螺栓对螺栓孔的反作用和右边地基对底板的作用，列出底板受力平衡式，即

M=F₁l₁+F₂l₂+…+F_zl_z （5-12）

因为各螺栓拉伸变形量与其中心到底板翻转轴线距离成正比，又因螺栓材料、直径、长度相同，剪切刚度也相同，所以剪切力也与距离成正比（胡克定律），即

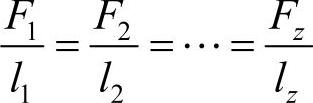
为了减少未知数，将各个螺栓受的力都写成受力最大螺栓受的力F₁的函数，即

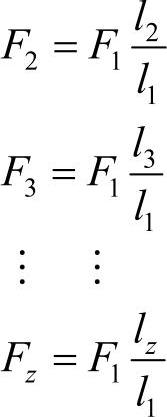
带入式（5-12）得

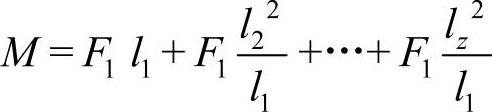
故最大工作拉力为