在霍普菲尔德网络中，模拟退火相当于对更新进行“加热”，这样能量就能在能量表面自由上下。因为单元在高温下可以随机反转，如果温度逐渐降低，霍普菲尔德网络很有可能在温度为零时收敛到能量最低状态。在实际操作中，模拟会在常温条件下让网络达到平衡状态，这样网络就可以访问周围的若干状态，并且在一个更广阔的范围内搜寻可能的答案。

例如，图7-3 中剪影的图案是存在争议的。这取决于你关注的是哪个部分，你可能会看到一个花瓶或两张侧脸，但不会同时看到这两种图案。问题的关键在于，你将哪部分看成图形，哪部分看成背景。我们设计了一个玻尔兹曼机网络来模仿这个基于图形—背景的决定（figure-ground decision），14用一些单元代表被关注的图形，其他单元代表图形的边缘。我们已经知道，视觉皮层中存在由边缘激活的简单细胞，但是图形可能位于边缘的任意一侧。我们的玻尔兹曼机网络通过两组边缘单元实现了图形选择，每组单元只支持一侧的图形。这类神经元随后在视觉皮层中被发现，被称为“边界归属细胞”（borderownerships cells）。15

玻尔兹曼网络中的约束可以通过手动设置权重来实现（图7-4）。在图形单元之间存在兴奋连接，而在边缘单元之间存在着抑制连接。边缘单元与它们所指向的图形单元之间存在兴奋性连接，能够支持图形单元，并与相背离的图形单元间形成抑制性连接。^[2]注意力是通过对一些图形单位产生偏倚（bias）而实现的。当玻尔兹曼网络对单元使用霍普菲尔德更新规则时，它会落入局部能量最小值，这些局部能量最小值在本地图块中一致，但在全局上并不一致。当更新中加入了噪声时，玻尔兹曼网络可以跳出局部最小值，并且通过缓慢退火降低噪声温度，这样一来网络的能量函数就可能得到全局一致的能量最小值（见图7-4）。由于更新是异步和独立的，因此网络可以由具有数百万个单元并行工作的计算机来实现，并且可以比一次按顺序执行一个操作的数字计算机更快地收敛到解决方案中。

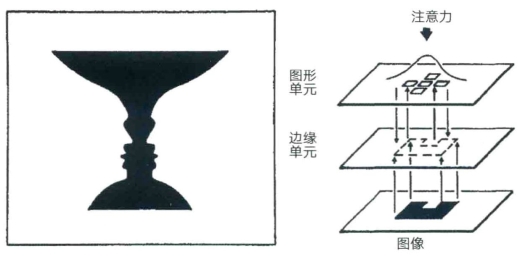
图7-3　模棱两可的图形—背景问题。（左图）如果关注黑色图形，你看到的是一个有白色背景的花瓶。如果关注的是白色背景，那你会看到两张互相注视的脸。你可以来回变换视角，但是做不到同时看到两种图案。（右图）图形—背景网络模型。两种单元分别代表了物体的边缘（线段），和某个像素是否属于图形或者背景（方块）。图像输入方向为从下到上，注意力输入方向是从上到下。其中，当某个区域应该被当作图形而进行填充时，注意力就是针对该区域所产生的偏倚。图片来源：P.K.Kienker，T.J.Sejnowski，G.E.Hinton，and L.E Schumacher，“Separating Figure from Ground with a Parallel Network，”Perception 15（1986）：197-216，left：figure 1；right：figure 2。(www.daowen.com)

图7-4　正在分离图形与背景的玻尔兹曼机。（上图）网络中的方形单元为标识图形的图形单元，三角形为标识轮廓的边界单元，连接单元的正负属性也被一同标出。边缘单元可以指向或者背离图形。（下图）（a）关注于图形C内部区域的网络示意图。温度^[3]刚开始很高，单元在开启和关闭状态之间不停变换。（b）随着温度下降，在指向内部的边缘单元的支持下，C内部的图形单元开始聚拢；同时，注意区以外或没有边缘输入的单位开始消失。（c）当温度为零时，注意区的图案被填满。（d）如果注意区移向外围，重复该过程，则外部区域会被填充。图片来源：P.K Kienker，T.J.Sejnowski，G.E.Hinton，and L.E.Schumacher，“Separating Figure from Ground with a Parallel Network，”Perception 15（1986）：197-216，below：figure 6；above：figure 3。

那个时候，我已经在哈佛医学院的斯蒂芬·库夫勒那里完成了博士后研究，在约翰·霍普金斯大学（位于巴尔的摩市）生物物理系开始了我的第一份工作；杰弗里·辛顿在卡内基-梅隆大学（位于匹兹堡市）计算机科学系担任教职，在那里他很幸运地得到了艾伦·纽维尔的支持，艾伦对人工智能的新方向持十分开放的态度。匹兹堡和巴尔的摩离得很近，所以杰弗里和我可以在周末见面。我们将这一霍普菲尔德网络的新版本称为“玻尔兹曼机”，以致敬19 世纪的物理学家路德维希·玻尔兹曼（Ludwig Boltzmann），他是统计力学的创始人。我们的波动性神经网络模型就是借助统计力学的工具进行分析的，之后我们很快就发现，该模型也是一个强大的学习机器。

在恒定的“温度”下，玻尔兹曼机会达到平衡。在平衡状态下会发生一些神奇的事情：多层神经网络学习的大门将被打开。而此前，每个人都认为它的存在有弊无利。有一天，杰弗里给我打电话，说他刚刚从玻尔兹曼机衍生出一个简单的学习算法。该算法的目标是执行从输入单元到输出单元的映射。但与感知器不同的是，玻尔兹曼机在输入和输出层之间也存在一些单元，我们称之为“隐藏单元”（见方框7.2）。通过对其呈现输入—输出对和应用学习算法，玻尔兹曼网络学会了实现目标映射。但是，其目标不仅仅是要记住输入—输出对，也要将没有被用于训练网络的新输入正确地进行分类。此外，玻尔兹曼机也在通过其持续不断的波动状态来学习概率分布——对于一个给定的输入模式，每个输出状态的访问频率如何——这就使其具备了生成性：学习之后，它可以通过钳制每个输出类别来生成新的输入样本。