1983 年的夏天，辛顿、霍普菲尔德和我参加了杰罗姆·费尔德曼在罗切斯特大学组织的一场讨论会。霍普菲尔德告诉我们，他解决了一种强交互网络的收敛问题。他证明了一种独特的非线性网络模型，即现在的“霍普菲尔德网络”，能确保收敛到一种叫“吸引子”（attractor）的稳定状态（见图7-2，方框7.1）7（高度非线性网络很容易发生振荡，或表现出更多的混沌行为）。此外，可以通过选择网络中的权重，把吸引子状态做成信息内容。如此一来，霍普菲尔德网络就可以被用来实现一种“内容可寻址存储”（content-addressable memory）。存储的信息可以只用信息内容的一部分作为提取输入，让神经网络完成信息填充。这让人联想起了人的记忆行为。如果我们看到某个熟人的脸，就能想起那个人的名字和先前与之交谈过的内容。

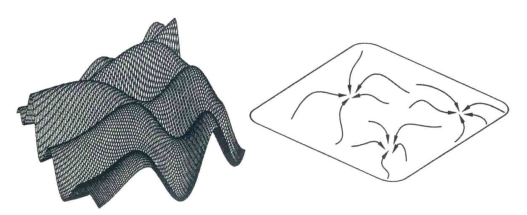
图7-2　霍普菲尔德网络的能量场景图。（左图）网络的状态可以被看作是能量表面上的一个点。（右图）每次更新可以将状态移动到其中一个局部能量最小值，叫作“吸引子状态”。图片来源：A.Krogh，J.Hertz，and R.G.Palmer，Introduction to the Theory of Neural Computation Redwood City CA：Addison-Wesley，1991，left：figure 2.6；right：figure 2.2(www.daowen.com)

霍普菲尔德网络的重大突破性在于，它能在数学上保证收敛。研究人员曾认为要分析高度非线性网络的一般情况是不可能的。当网络中的所有单元被同时更新的时候，所引发的动态情况非常复杂，没有办法保证收敛。8但是霍普菲尔德网络展示出，当网络中单元的更新是顺序进行的时候，一种单元组彼此双向连接并且权重相同的特殊对称网络，是可解，并且最终是能够收敛的。

越来越多的证据表明，海马体（保存关于特殊事件和独特对象长期记忆的大脑关键区域）中的神经网络存在像霍普菲尔德网络中的那种吸引子状态。9 虽然霍普菲尔德模型非常抽象，但它的本质行为和在海马体上观察到的行为十分相似。20世纪80年代，许多物理学家都曾利用霍普菲尔德网络实现了由物理学到神经科学的跨越。使用理论物理的复杂工具来分析神经网络和学习算法的过程中，诞生了很多惊人的发现。物理、计算和学习在神经科学理论领域深刻地联系在一起，这一结合成功地实现了对大脑功能的诠释。

约翰·霍普菲尔德和当时在贝尔实验室的大卫·汤克（David Tank），随后又展示了一种霍普菲尔德网络的变体，其中的单元可以拥有0到1之间的连续值，^[1]能够很好地解决优化问题，例如“旅行商问题”（traveling salesman problem），该问题旨在寻找能够访问多个城市的最短路径，每个城市仅访问一次。10 这是一个计算机科学领域众所周知的难题。网络的能量函数包含了路径的长度，限制是每个城市仅能访问一次。经过初始状态，霍普菲尔德和汤克的网络能最终收敛到一个最小能量状态，表明找到了一条较好的路径，虽然不一定是最佳路径。