通常向心涡轮机叶轮叶片的进口段为径向直叶片，进口段之后为旋转导向叶片。叶轮的旋转导向叶片部分又常被称为导风轮。在设计叶轮的型线时，叶片前后两部分的设计可以分别进行。叶轮的型线设计工作可分为三个步骤：①在z-r面内对叶轮子午面型线进行设计；②在z-θ面内对叶轮型线进行设计；③以叶片的中心曲面型线为基础，设计压力面和吸力面的型线。

1.子午面型线的设计

对于一个叶轮来说，其子午面的轮廓线对叶轮通道内流场有着非常大的影响。因此，设计出一个合理的叶轮子午面型线成了设计叶轮的关键。子午面的示意图如图3-62所示。从图中可以看出，叶轮子午面型线主要由以下几个参数和曲线所决定：

（1）叶轮进口处顶部半径R_tR_t可以说是向心涡轮机最重要的几何参数。影响R_l的因素很多，主要有向心涡轮机焓的大小以及转速等。此外，结构和强度的要求也影响着R_t的选取。

（2）叶轮进口宽度l_t它与叶轮进口处顶部半径、工质的质量流量和叶轮入口处的绝对速度等因素有着密切的关系。通常，叶轮入口的相对叶高l_t不低于l_tmin＝（l_t/2R_t）min＝0.02～0.04。

图3-62 向心涡轮机叶轮子午面示意图

（3）叶轮出口根部半径R_2h和顶部半径R_2sh它们决定了叶轮出口面积的大小。R_2h值越小，则出口的平均半径也越小，对向心涡轮机性能的提高有利；但出于强度方面的原因，R_2h值有其下限。目前向心涡轮机的相对根径D_2h≥0.1～0.15；相对顶径D_2sh≤0.85～0.90。

（4）叶轮轴向长度Z 它对子午面的内外轮廓线有着直接的影响。Z有一个最小值，当它小于这个值时，会使气流从径向到轴向转折的距离过短，造成流动情况的恶化。根据参考文献［30］，Z值一般取为叶轮出出口平均半径的1.1～1.3倍比较合适。由参考文献［32］和［37］可知，导风轮轴向长度Z_m与叶片的曲面曲率有关，对叶轮内的流动有重要影响。

（5）子午面的内、外轮廓线 内、外轮廓线决定着叶轮通道内气流由径向转为轴向的运动过程。为了获得较高的流动效率，不仅要求内、外轮廓线自身光滑连续，还要求两者之间通道空间的变化平稳、顺滑。

在上述的几何参数和曲线中，R_t、l_t、Z、R_2h、R_2sh已经由向心涡轮机的一元热力设计得到。于是，设计子午型线的工作就只剩下内外轮廓线的设计。通常先设计内轮廓线：在设计时先取若干个控制点（一般要5个左右）并用样条曲线拟合，然后由连续性方程算出通道的法向宽度，求得外轮廓线上点的坐标，进行修正使其通道法向宽度基本上呈现线性变化，进行样条曲线拟合可得到外轮廓线。为了便于合作单位制造加工，最后，将内、外轮廓线处理成多段圆弧和直线段连接构成的形式。本文将外轮廓线处理成由三段圆弧和两段直线段构成，将内轮廓线处理成由两段圆弧和两段直线段构成。

2.z-θ面内型线的设计

前面提到，叶轮的径向进口段和后面的曲面部分可以分别设计。由于径向直叶片的设计相当简单，所以这里只介绍曲面部分，即导风轮叶片的造型。

在高速向心式涡轮机和离心式压缩机的叶轮设计中，导风轮叶片的造型问题十分重要。导风轮的几何性质决定了叶片的气动性能、强度特性及工艺性能。对于导风轮的叶型基本要求如下：

1）具有良好的空气动力性能。

2）其排气边（离心式压缩机叶轮的进气边）的几何形状能够满足该处气流流型要求。

3）成型后的叶片应具有较好的强度特性。

4）叶型便于加工和检验，通用性较强。

原则上，导风轮的叶型可以按各种曲面成型，但是并不是所有的曲面都能满足气动、强度和工艺等方面的要求。导风轮曾采用圆柱面、圆锥面来造型，这些曲面容易加工，但是它们的气动性能较差。因此，它们逐渐被抛物面所取代。经研究分析发现，平基面非可展直纹抛物面，对于导风轮叶片造型来讲是一种比较理想的曲面，它基本上能够满足导风轮各方面的要求。因此，对导风轮叶片中心曲面部分的设计，采用平基面、非可展直纹抛物面造型方法来进行。

向心涡轮机叶轮的叶片造型采用的型面为平基面、非可展直纹抛物面。抛物面方程式可以用各种不同的坐标给出，习惯上采用直角坐标系。从图3-63a中可见，H为原点给出一个直角坐标系H，X，Y，Z。在其中取一个与ZHY面平行且与之相距X_p的P平面。在图上取两个与P平面垂直的平面Q和Q′，两平面相互平行，彼此相距Z_m。在空间取一根和Z轴平行的直线，它和Q，Q′两面分别相交于O及O′。OO′线和ZHY面之间的距离为X₀。如果在空间内始终平行于Q面移动一条直线，并令此直线的一端从O点开始沿OO′滑动，而令直线的另一端沿P面上的抛物线滑动，则此线在空间内形成的曲面即是非可展直纹抛物面（以下简称抛物面）。OO′称为抛物面的形成轴，但并不一定用作叶轮的旋转轴。向心涡轮机叶轮叶片若按此抛物面成型，则与P面平行的任一平面（如图中的I面）和该抛物面的截交线，都是与基面上的抛物线同次的抛物线，这是此曲面的一个非常重要的性质。若令此抛物面围绕某一固定轴O₀O₀′旋转，即成为导风轮的一个叶片的型面。对于向心涡轮机导风轮而言，其排气边的坐落于Q′面上B_P′Q′线上，其进气边为A_PQ。在离心式压缩机的导风轮上，两者位置正好相反。导风轮的轴心线O₀O₀′应与OO′平行，并且处于ZHY面上。根据叶型设计的需要，OO′轴的位置可以处于O₀O₀′的上方、下方或与O₀O₀′重合。P称为基面，X₀称为移轴量。当OO′轴的位置与O₀O₀′重合时，X₀＝0，称为非移轴叶型。采用非移轴叶型的设计结构对叶轮的强度较为有利。图3-63b示出了图3-63a在Q面上的抛物面投影图。

在图3-63a上取两个平面：I平面及J平面。I平面是与P面平行的任意平面。其方程式为X_t＝常数。J平面是与Q面平行的任意平面，其方程式为Z_j＝常数，由抛物面的形成原理可知，J面和抛物面的交线C_piQ_j是抛物面上的任意一点，只要找到此点（X_i，Y_ij，Z_j）坐标之间的关系，就建立了整个抛物面的方程式。在P

图3-63 非可展直纹抛物面的形成及其在Q面上的抛物面投影图

a）非可展直纹抛物面的形成 b）Q面上的抛物面投影图

面上从RP点开始给制一条抛物线。已知当X_i＝X_p时抛物线的方程为

Y_p＝a_pZ^t （3-87）

设Z_m为倒风轮抛物面叶型部分的最大轴向尺寸，当Z＝Z_m时，Y_p值为

当X_t＝X_o时，

Y_o＝（X_p－X_o）·tan θ

这就是抛物面轴OO′处的等Y面的方程式。接下来确定C_ij点的Y_ij值。为便于分析，将整个抛物面及形成线投影到Q面上，如图3-61a。则

X_t为一常数的I平面与抛物面的截交线方程式为

其中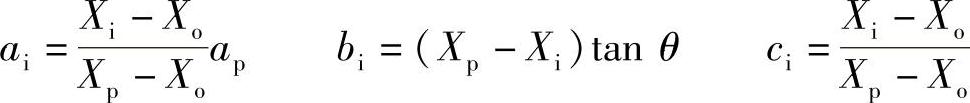

整个抛物面的数学表示式为

Y＝b＋aZ^t＝b＋c·a_pZ^t

式中a、b和c都只是X的函数，叶型的背、腹二抛物面分别以O₁O′₁和O₂O₂′为轴成型，并且中心抛物面对称分布。叶片进气边的Y向厚度用2m_i表示，排气边的Y向厚度用2n_i表示。这样，在I截面上可得到三条抛物线，其方程式为

Y_i＝b_i＋a_iZ^tY_if＝b_i＋a_ibZ^t＋n_iY_ib＝b_i＋a_ibZ^t－n_i

其中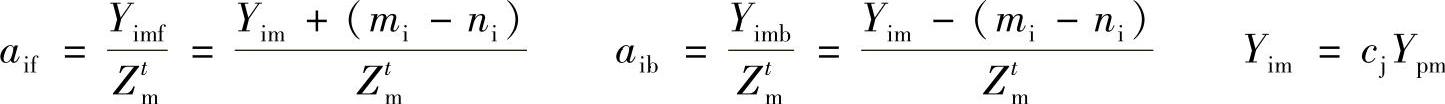式中，下标f表示叶片腹面；b表示背抛物面。

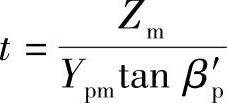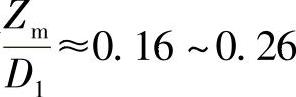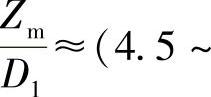
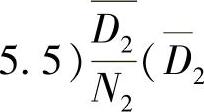t与导风轮的轴向长度Z_m的关系为（β_p′为P面上导风轮叶片出口角）。在设计导风轮的叶型抛物面时，如果指数t选择不当，则可能出现气流转弯过急和流道当量扩张角过大的情况；也可能出现相反的情况，即气流虽沿抛物面平缓转向，但是导风轮的轴向尺寸Z_m变得太大，叶轮形状就变得粗胖起来，结果在流道的子午面成型中可能会出现一些困难。一般的有及为叶轮的轮径比，N₂为叶轮出口叶片数，D₁为叶轮外直径）。如果Z_m值太大时，可重设t重新计算。

3.叶片压力面、吸力面的设计(www.daowen.com)

确定了叶轮的中心抛物面以后，应给抛物面加上叶片厚度的变化规律以完成压力面、吸力面的设计。叶片的厚度的变化应满足强度和振动的要求，应从叶根到叶顶方向逐渐减薄，从进气边到排气边方向逐渐减薄。叶型的背、腹两抛物面相对中心抛物面对称分布。如果导风轮叶片进气边的Y向厚度用2m表示，排气边的Y向厚度用2n表示，那么在中心抛物面的同一坐标系下，背、腹二抛物面的方程式如下：

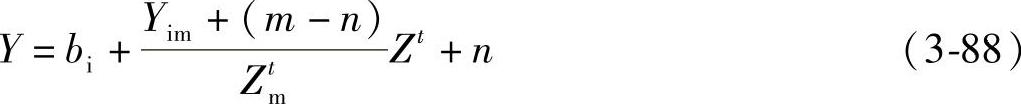腹面背面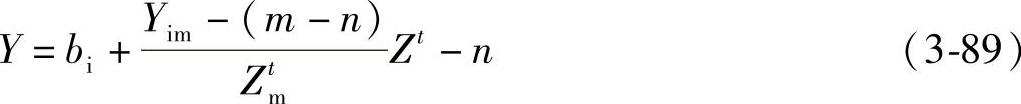

至此就完成了向心涡轮机导风轮叶片的叶型设计。

4.导向叶栅的结构设计

工质在进入向心涡轮机后先在导向装置中膨胀加速，然后再流入叶轮驱动叶轮旋转做功。导向装置的主要作用是使工质所具有的能量能够高效率的转变成动能，并保证工质在叶轮的入口截面上能够获得所需要的流速c_l和流动方向α_l。某型向心涡轮机的导向装置由进气蜗壳和导向叶栅（又称喷嘴环）组成。

导向叶栅如图3-64所示。它由若干个导向叶片组成，各个叶片等距的安置在叶轮四周，从而形成一个环形的定子叶栅。气体在导向叶栅通道中压力与温度下降，流速不断升高，在出口截面流速达到c_lN周向平均气流角为α_lN。在导向叶栅的出口，流场相当不均匀，沿着圆周方向气流的速度和方向都具有较强的脉动性质。显然这种极不均匀的气流直接进入叶轮，将给叶轮的工作带来一些不良的影响。在导向叶栅出口和叶轮进口之间设有一定的径向间隙Δ＝r_n－r_l，可使进入叶轮的气流变得更为均匀。气流在环状径向间隙中的运动轨迹，可以近似地认为是一条对数螺线，也就是可以认为在间隙中气流的流动角为一常数，不随半径变化，即α_lN≈α_l。在r_l处的c_l略大于喷嘴环出口的c_lN，不过两者相差甚微，故一般近似认为气流诸参数在径向间隙内不发生任何变化，即假定α_lN＝α_l，c_lN＝c_l。当环状径向间隙足够大时（例如8mm左右），通过质点间的能量交换作用，在径向间隙出口气流的流场趋于一致。此外，适当的环状径向间隙，对于降低向心涡轮机运行时的噪声和减轻导叶的冲蚀具有显著作用。

根据热力计算和上述假设，可以得出导向叶栅进、出口的结构参数和气动参数。在确定了导向叶栅结构参数后，来选择导向叶栅的叶型。首先要确定叶片的中弧线。通常中弧线有单圆弧、双圆弧和抛物线等线型。根据导向叶栅的内外径、叶片的入口角和出口角可以确定导向叶栅的中弧线。

图3-64 导向叶栅示意图

图3-65 蜗壳截面示意图

5.进气蜗壳的设计

图3-65为蜗壳截面示意图。向心涡轮机的进气蜗壳由进气段、蜗管和环形加速段构成，蜗管截面的形状有许多种，如矩形、圆形、椭圆形，梯形及梨形等。由于蜗壳中的流动具有三维性质，为了描绘这种流动，必须采用一些近似假设以使问题得以简化。根据所使用的简化条件不同，可分为一元分析方法和二元分析方法。这里使用二元分析方法。假设蜗壳内的流动为绝热定常流动，工质为理想气体，其粘性作用用速度系数φ来表示。近似认为蜗管内气流的角动量按等环量变化，即c_θuR_θφ＝c_1uR_d＝常数。二元分析方法的基本方程为

无论蜗管的截面是什么形状，都可以用式（3-90）计算。方程的右边由一些已知的数据组成，解此方程的问题就归结于求方程左边积分表达式的问题。当采用梯形截面时，则

由于实际所用的蜗管横截面为带有圆角的梯形，所以必须对式（3-91）计算出的h值进行修正。蜗管的计算公式推导如下：

1）假定气体为理想气体。其粘性作用将用速度系数φ表示。

2）假设流动过程为定常、绝热、等熵过程，则

式中，θ为截面的方位角。

3）设通过蜗管任一截面的工质的流量G_θ与方位角θ呈下列关系：

式中，G为蜗管进口处的流量，θ_max为蜗管截面的最大方位角。

4）近似认为蜗管内气流的角动量按等环量规律变化，则

c_θuR_θφ＝c_1uR_d＝常数（3^-95）

此外，由连续方程得

式中，Γ为部分进气度。

由式（3-94）、式（3-98）求出截面的几何尺寸：

由式（3-95）得

将式（3-100）代入式（3-99），得

由于p/p^κ＝常数，气体状态方程为

所以

蜗管的截面形状有许多种，例如矩形、椭圆形、梯形等。现推导梯形截面的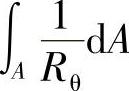表达式。

图3-66 梯形截面公式推导用图

（1）梯形截面（图3-66）

所以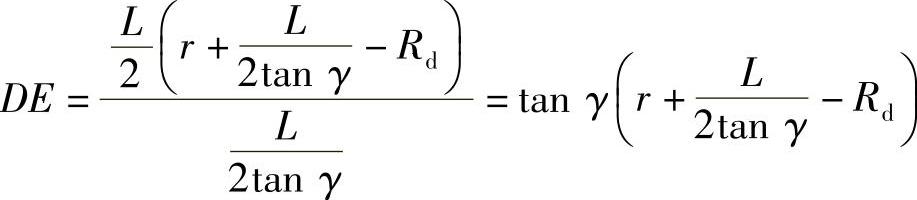

（2）梯形截面圆角的修正

图3-67 梯形截面圆周角修正公式推导用图

设图3-67的右图中，非阴影区域面积与梯形P′Q′S′RP′面积之比为A_s。

因为