离心式压缩机流通部分的损失计算，在无冷却时忽略气体与外部热交换，存在如下关系：

式中，ψ为叶轮速度系数；η为效率；φ为导向装置速度系数；w为无粘性气流速度；R_a为表面粗糙度；M_a为马赫数；R_e为雷诺数。

对损失的分析采用通流中各部分速度分布来描述。在马赫数M_a和雷诺数R_e自动模化时，表面损失仅由相对速度分布决定阻力系数c_w，即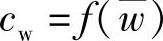。无粘性气流速度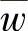的分布与附面层参数的关系，可表示为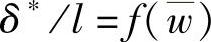若引进平均速度w_m和b_m，则阻力为

其中c_w＝x₁＋x₂k^x_w3 k_w＝w₂/w₁

叶片表面的流动，因旋转和弯曲受二次流和不稳定性的影响，二次流强度通常与体积力有关。如轴流压缩机二次流阻力系数c_wsec与体积力系数c_α的关系是：

为了考虑二次流和不稳定的影响，引入修正因子（1＋x₄c^x_α3）。同时考虑马赫数M_a，雷诺数R_e，表面粗糙度R_a的影响，叶片表面阻力系数为

c_wb＝（x₁＋x₂k^x_w3）（1＋x₄c^x_z5）（1＋x₆M^x7）（1＋x₈R^x_e9）（1＋x₁₀R^x_a11） （3-74）

除了气流参数外，还应该考虑到几何参数。叶轮通道在从叶片的阻力p_wb过渡到损失系数ξ_b时：

p_wb＝c_wb lb_mρm（ω²_m/2） （3-75）

则损失系数表达为

ξ_b＝c_wb（l/α_m）（w_m/w₁） （3-76）

这样式（3-73）就可变化如下形式：(www.daowen.com)

离心式压缩机的数学计算模型是很复杂的，其系数x_i由级通流部分的各元件决定，这里主要是确定任意叶栅中的翼型损失。翼型损失通过叶片上G条带区的损失求和：

第j带区的损失系数由下式决定：

翼型损失采用量纲为1形式，Δη_wb＝h_wb/h_ih，并考虑q_m＝ρϕπu₂D²₂/4和h_ih＝φ_θ2u²₂，则

将轮盘、轮盖壁面也分成G条带区，每条带区又分成L段，则

为寻找c_w0，来研究哥式加速度2ωw_se的分量在w方向及垂直壁面方向上的投影。得到轮盖的阻力系数为

c_wsh＝cwshb（1^－x i c^x α^i＋1 cos γ）（1－x_i＋2c^x_αi＋2 sin γ） （3-82）

轮盘阻力系数为

当有二次流时，哥式加速度的分量2ωw_se影响到流动条件。在w_seb从轮盘指向轮盖时为

计算损失能量头或阻力有许多经验公式，例如：

沿叶道四个面的二次流使量纲为1的二次流损失为：

上述公式为任意叶栅的数学计算模型，是所有通流部分中损失计算的基础。静止叶栅忽略其中与哥式加速度有关的修正项。对于半开式叶轮，还应该考虑叶顶泄漏所引起的损失。