离心压缩机叶轮的结构设计主要有叶轮子午流道设计和叶轮叶片型面设计。子午流道设计传统上的设计方法,一般是根据离心压缩机叶轮热力性能计算,利用经验数据经过多次修正得到结果。叶轮叶片型面设计根据所采用的叶片形状不同而有不同的设计方法。本书主要采用径一轴流离心压缩机圆柱直纹抛物面的叶型设计方法进行计算。
1.离心压缩机叶轮子午气道设计
离心压缩机结构设计的目的不仅在给定的流量、转速、进出口参数的情况下,确定压缩机各截面上的基本结构尺寸,而且要求设计出的压缩机具有效率高、工作可靠、性能符合要求、结构合理及加工工艺性好等特点。
压缩机结构设计首先必须根据压缩机性能热力计算、按照加工条件设计出叶轮的子午流道。在确定结构参数及子午流道形状时,除了必须保证热力计算时所要求的热力参数外,还要注意减少流动损失。因此,必须合理地选择叶片数、子午流道的曲率及结构尺寸之间的相互配合。在以一元流动为基础的离心压缩机设计中,子午面形状一般是在经验数据的基础上,逐步修正为光滑变动的通道来确定。如图3-49所示的离心式压缩机气道,其有关的尺寸可以按下列参数进行估取:
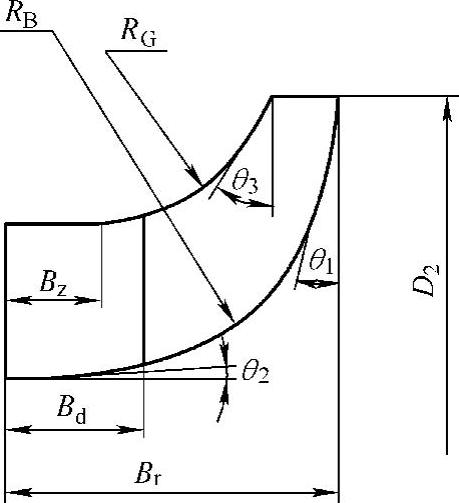
图3-49 离心式压缩机气道
1)叶轮叶轮轴向宽度:
Br=(0.22~0.35)D2 (3-48)
2)导风轮轴向宽度:

4)轮盘(毂)基线出口倾斜角θ1=3.5°~15°。
5)轮盖基线进口直线段长度约为0.5BD。
6)轮盖基线进口倾斜角θ3=15°~20°。
7)轮盘(毂)基线中间过渡圆弧半径:
RB=(0.25~0.5)D2(3-50)
8)轮盖基线中间过渡圆弧半径RC≈0.1D2。
轮盘基线中间过渡圆弧半径不宜用过小的曲率半径,否则将使叶轮损失增加。传统的结构设计方法中,子午面形状必须在展开后用包络线校核,要求两侧面平顺并接近直线。如果包络线不够平顺,要改变子午面的曲率半径,重新调整直到符合要求。这样的设计方法比较粗糙,误差相对来讲也比较大,并且设计周期较长。应该考虑采用结构优化方法进行设计。
2.离心压缩机叶轮叶片型面设计
离心压缩机的叶片型线可以分为工作轮径向直叶片和导风轮叶片两部分。在抛物线导风轮叶片中,可以分为平面抛物线叶片和圆柱面抛物线叶片。前者是用平面上的抛物线去形成叶片型面,因此用平面去切割这类导风轮叶片时,所得的交线是抛物线;后者是用圆柱面上的抛物线去构成叶片型面,所以如果用圆柱面去截取这类导风轮叶片,得到的交线就是圆柱面上的抛物线。
用抛物线形成的叶片抛物面,按其几何性质又可分为直纹抛物面和非直纹抛物面两种。直纹抛物面的形成是取一基面(平面或圆柱面)上的抛物面及一根平行于基面的轴,以一根直线作为母线始终垂直于轴并作沿着此抛物线及轴的滑动,所得到的此根直线的轨迹就是直纹抛物面。非直纹抛物面是不能用直线来形成的。
在叶轮的造型中,通过叶轮旋转轴的平面为子午面,垂直于叶轮旋转轴的平面叫作径向面,而垂直于叶轮旋转轴的端面称为径向端面。具有两个倾斜端面的导风轮圆柱抛物线叶片的造型方法已经得到广泛地应用。图3-50为具有两个倾斜端面导风轮的叶片示意图。图3-50为叶片型面在径向面上的投影。采用R、θ、Z的圆柱坐标系统,原点O选在叶轮旋转轴上。θ角及径向面上的圆弧长度Y取与叶轮旋转方向相同时为正值,反之则为负值,且都从工作轮叶片中面起算。ψ为中心抛物面与外端面的相交直线和其平均半径处的径向线间夹角的轴向投影,取使叶片顶部包角减小的ψ角为正值。
中心抛物面在圆柱截面上的抛物线公式表示为
Y=azt (3-51)
式中,Y为圆柱截面上叶型中心抛物线在径向面上的圆弧长度,它从工作轮叶片中面起算;a为抛物线方程的系数,它是半径R的函数;t为抛物线方程的指数,它是一个常数。
中心抛物线与径向面之间的角度可看作叶片的角度β0B。为了与热力计算统一,它仍代表中心抛物线与径向面之间的夹角,其值随半径R和轴向坐标Z而变化
(1)抛物线方程指数的确定 为了确定抛物线方程的指数,首先要建立抛物线方程指数和叶片角度之间的关系。可以得出叶片角度与叶型中心抛物线在径向面上的最大圆弧长度YOM、叶片轴向长度Z0、抛物线方程的指数t以及距离导风轮内端面的轴向距离Zt等值有关。
再由导风轮外端面上中心抛物线与径向面间的夹角,以及导风轮外端面平均半径处叶型中心线所占的径向面上的最大圆弧长度与其在圆周方向的最大包角的关系式,化简即可得到抛物线方程的指数。
(2)导风轮叶片角度的计算 叶片角度是指中心抛物线与径向面间所成的角度。对式(3-51)求导可得

而

将抛物线方程的系数代入,并经过化简可以得到具有两个径向端面的导风轮的中心抛物面所采用外端面叶片角度的计算公式为(www.daowen.com)

图3-50 具有两个倾斜端面导风轮的叶片示意图
式中,RM为导风轮外端面平均半径;R为导风轮外端面任意一点的半径;β0B0为导风轮外端面任意一点的叶片角度;β0BOM为导风轮外端面平均半径处的叶片角度。
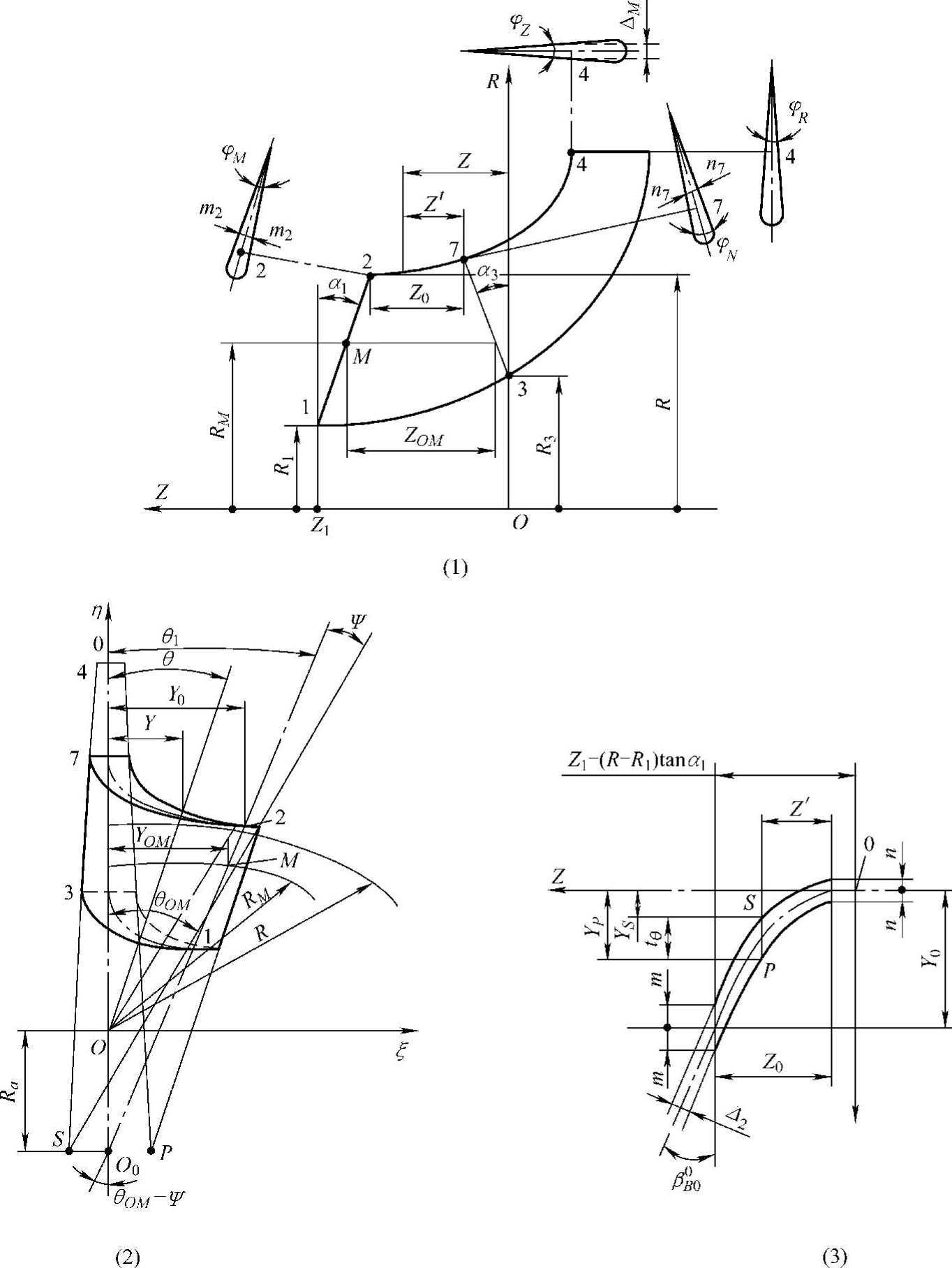
(3)导风轮叶型周向厚度方程 在中心抛物面的基础上,可以推出相应的内外弧抛物面的方程。在以半径为R的圆柱面的展开图上,如图3-50所示,在导风轮内端面处,内外弧抛物线的原点与中心抛物线的原点O分别在正负Y向移动一个叶型的周向一半厚度n的距离;在导风轮的外端面处,外端面与内外弧抛物线的交点分别与中心抛物线的交点向前和向后移动了一个叶型的周向半厚度m。
在半径为R的圆柱面上,根据内外弧抛物线在径向面上的最大圆弧长度,可以求得内外弧抛物面方程的系数ap和as。内外弧抛物线在径向面上的圆弧长度分别为
Yp=apZ′t+n (3-55)
Ys=asZ′t-n (3-56)
由于导风轮叶型的周向厚度tθ=YP-YS,因此可以求出其叶型的周向厚度tθ。导风轮内外端面处叶型的周向—半厚度n和m是随半径R变化的,根据工艺和强度条件可以选定导风轮外端面平均半径及顶部叶片的真实厚度ΔM和Δ2,再由导风轮外端面与内外弧抛物面的相交直线的夹角φM与ΔM及Δ2的关系,就可以得出导风轮外端面处叶型的周向半厚度m计算公式为
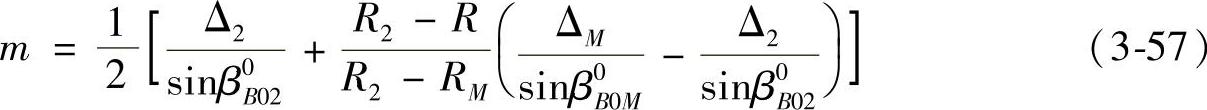
式中,R2为导风轮外端面叶尖处的半径;R为导风轮外端面任意处的半径;β0B02为导风轮外端面叶片顶部的角度。
根据工作轮叶片的角度φn,由导风轮内端面处叶根的叶型周向半厚度n3+ε,并根据其内外弧抛物面两相交直线夹角亦为φn的情况,向上即可推出内端面处任一半径R上叶型的周向半厚度n: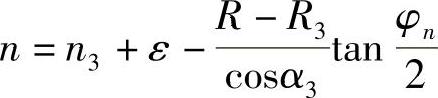
式中,n3为工作轮与导风轮交界面处工作轮叶片根部的半厚度;R3为导风轮叶片内端面根部的半径;ε为内端面处导风轮叶片半厚度与工作轮叶片半厚度的差值。
(4)导风轮叶型角坐标的确定 在叶论三元流动的计算中,需要提供导风轮叶型的角坐标。可以根据导风轮叶型中心抛物面的方程确定内外弧抛物面的角坐标。
导风轮叶型中心抛物面的方程式表示为角坐标θ=f(R,Z)的函数形式,具有两个径向端面的抛物面,其中心抛物面的方程经过计算可变为:

可以看出,θ角坐标与半径R无关,它只是轴向坐标Z的函数,这种中心抛物面是圆柱直纹抛物面,它适合于导风轮外端面处气流轴向的绝对速度均匀的情况,其相应的内外弧抛物面角坐标为:
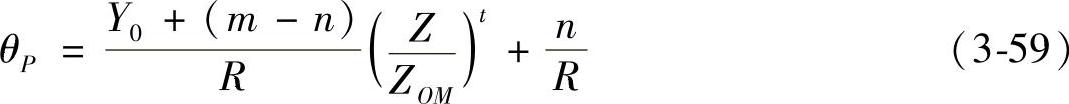
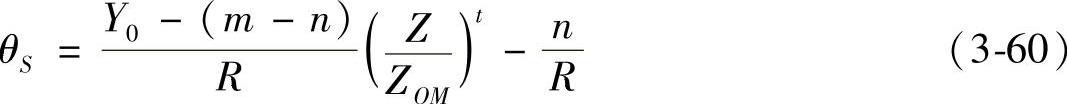
如图3-51所示,在径向面上任取某一工作轮叶片中线为纵坐标η,以η沿叶轮旋转方向转过π/2的轴为横坐标ξ,而以叶轮旋转轴O为坐标原点。O0为中心抛物面的轴,它与O轴的距离为Ra。取Ra使顶部叶片包角减小的为正值。S为外弧抛物面的轴,P为内弧抛物面的轴。ψ为导风轮外端面处叶片中线与其平均半径处径向线间的夹角(因为这时外端面为径向面,所以这个角与其轴向投影相等),也取使顶部叶片包角减小的为正。
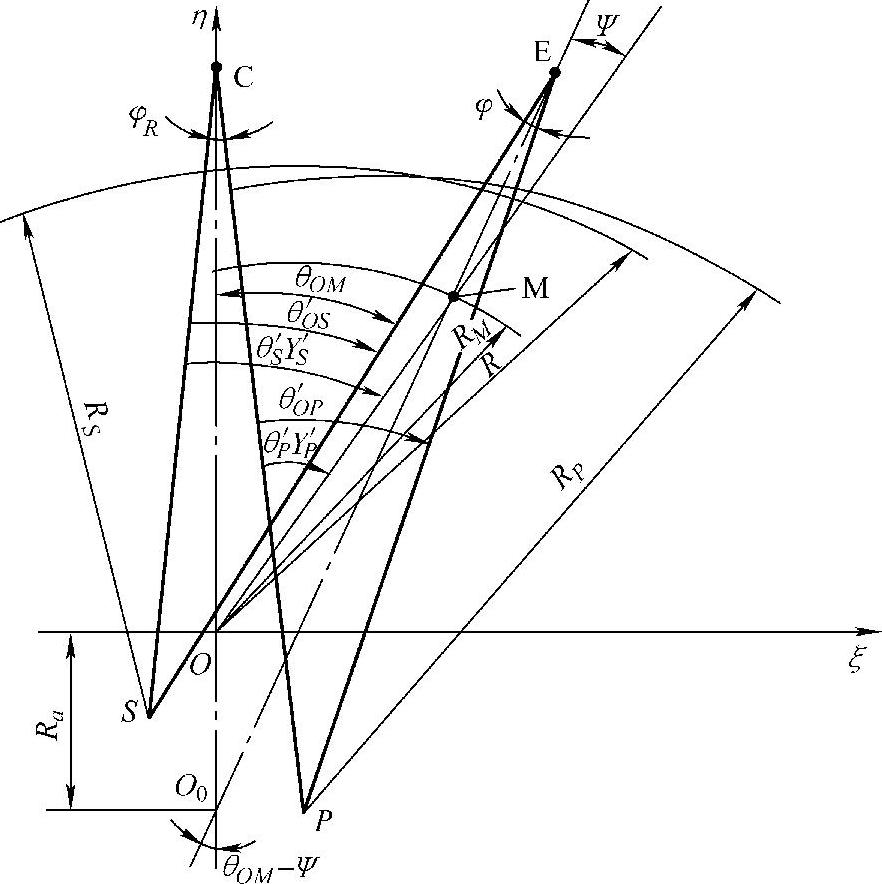
图3-51 叶片型面在径向的示意图
内弧圆柱直纹抛物面的角坐标θP′及其径向面上的圆弧长度YP′,都是从导风轮内端面与叶片内弧抛物面的交线起算。内弧抛物面在以P为中心的圆周方向上的最大距离为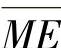 。同样,外弧圆柱直纹抛物面的角坐标θS′及其径向面上的圆弧长度YS′,都是从导风轮内端面与叶片外弧抛物面的交线起算。外弧抛物面在以S为中心的圆周方向的最大包角为θ′OS。
。同样,外弧圆柱直纹抛物面的角坐标θS′及其径向面上的圆弧长度YS′,都是从导风轮内端面与叶片外弧抛物面的交线起算。外弧抛物面在以S为中心的圆周方向的最大包角为θ′OS。
利用导风轮内端面叶根处叶型的周向半厚度n3和φR的值,求出C点的坐标;由三角形余弦定理求出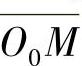 ;由mM和φm算出ME,进而由OE求得E点的坐标;再由PC和PE直线方程联立解出P点的坐标;由
;由mM和φm算出ME,进而由OE求得E点的坐标;再由PC和PE直线方程联立解出P点的坐标;由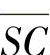 和
和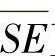 直线方程联立求解S点的坐标。
直线方程联立求解S点的坐标。
求出P和S的坐标后,再求这两个圆柱直纹抛物面的角坐标θP′和θS′与轴向坐标Z的关系式。为此,先求出内外弧抛物面在以P和S为中心的圆周方向的最大包角是θ′OP和θ′OS。它们分别为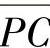 与
与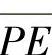 直线及
直线及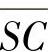 与S
与S 直线与ξ轴夹角之差。
直线与ξ轴夹角之差。
内外弧抛物面以O为圆心、以R为半径的圆柱面上,各自从内端面与内外弧抛物面的交线起算的。在径向面上的圆弧长度YP′和YS′分别为
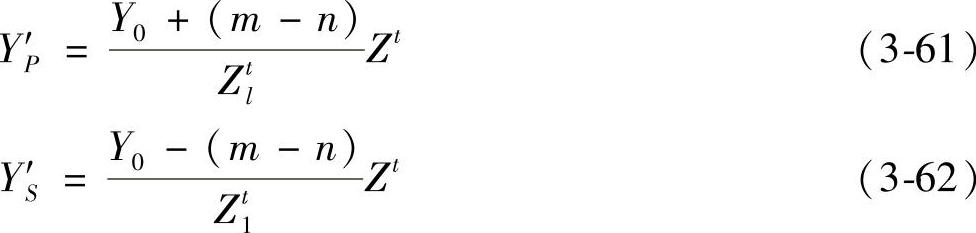
为了使以P和S为轴的圆柱直纹抛物面与内外弧抛物面近似,可分别在以P和S为圆心、以RP和RS为半径的圆柱面上,使其径向面上的圆弧长度与YP′和YS′相等的圆柱直纹抛物面,代替以O为轴的内外弧抛物面。这时的RP和RS可分别由它们在径向面上的最大圆弧长度与其相应的最大包角相除得出,即
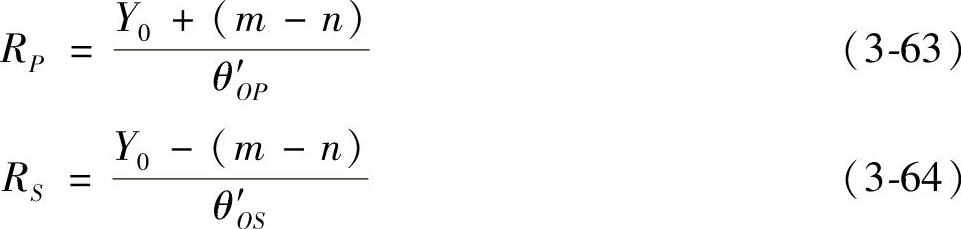
因为角坐标θP′=YP′/RP和θS′=YS′/RS,所以将式(3-61)至式(3-64)代入后,就可以得出这两个圆柱直纹抛物面的角坐标的关系式:
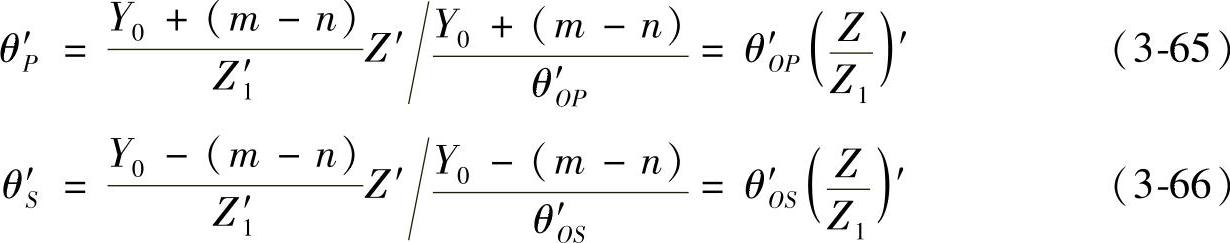
上述两式都与半径R无关,只是Z的函数。它们就是这两个圆柱直纹抛物面的表达式。计算框图见图3-50。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







