1.压缩机的压缩过程
在压缩过程中压缩机对空气压缩做功,必然要从外界获得一定量的压缩功,才能使空气的压力和温度上升,比体积缩小,以满足微型燃气轮机的要求。在理想绝热状态下,工质只与外界发生功的交换,而无热量的传递。这个没有热量传递的理想绝热过程使在没有摩擦和扰动等不可逆现象的理想情况下进行的。
在理想绝热过程中,工质的压力和比体积的变化规律为
psvκs=常数(3-1)
式中,κ为等熵指数,空气的等熵指数κ可以取1.4,燃气的κ取1.33。当工质按理想的绝热过程进行压缩时,过程中任一工况点上,工质压力p与其比体积v的κ次方的乘积彼此相等。即p1svκ1s=…=pisvκis=…=p2sv2κs。若已知过程初态的压力p1与比容v1、终态压力p2,由式(3-1)和理想气体状态方程pv=RT联解,可以计算终态的其他参数v2s与T2s。在理想绝热过程中,T与v之间的变化规律为
即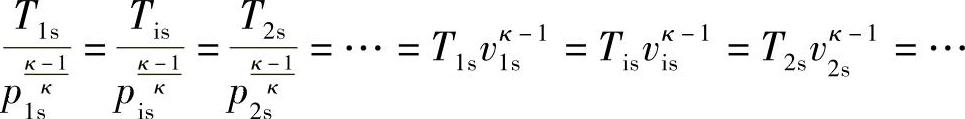
实际上理想的绝热压缩过程式不存在的。由于在压缩过程中不可避免的存在摩擦等不可逆现象,其结果将会产生一部分摩擦热qm转加给工质本身,致使工质的终态温度t2s和比体积v2s与都要比按理想绝热压缩过程压缩到同一终态压力p2s时所能达到的终态温度t2s和比体积v2s与大一些。同时,所需要给工质的实际压缩功也会有所增加。
从热力学观点来看,压缩过程与一个从外界吸收热量q=qm的多变压缩过程相当。因而,在实际的压缩过程中,工质终态的状态参数必须根据多变过程的规律计算:
式中,n为多变指数。对于压缩过程,n>κ,n值的大小与实际压缩过程中存在的不可逆现象的程度有关。一般在压缩机中,n=1.45~1.52。
实际上人们很少利用此个方法进行计算,而是引入一个能够比较直观地反映实际压缩过程中不可逆程度大小的绝热压缩效率ηc,来计算工质的终态温度t2s或T2s。
所谓绝热压缩效率ηcs,是指工质在理想的绝热压缩过程中所需吸收的压缩功Wcs,与实际压缩过程中达到同一终态压力时所需加给工质的实际压缩功Wc的比值,即
式中,Wc>Wcs。
当忽略工质比定压热容cp随温度改变而略微变化的特性时,式(3-4)可简化为
式中,T2s为理想绝热状况下的终态温度,T1为初始温度,T2为实际终态温度。在现代压缩机中,ηc=0.8~0.9。由此可见,只要已知压缩机的绝热压缩效率ηcs,就很容易求出压缩机出口工质的实际温度t2,进而可以求出比体积v2。
为了追求压缩过程计算的准确性,在实际计算中常采用特性曲线法进行计算。图3-37所示为生产厂商提供的某型压缩机稳态特性曲线。此特性曲线采用压比π、转速n、温度T和压力p、质量流量qm等来表示折合压比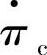 、折合转速
、折合转速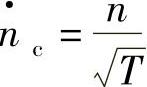 、折合流量
、折合流量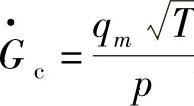 及折合效率
及折合效率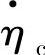 等。其关系式如下:
等。其关系式如下:
折合流量
效率
出口温度
功率 Pc=qm(h2-h1)/ηcj (3-8)
转矩
式中,qm为进入压缩机的空气质量流量(kg/s);p为压缩机进气总压力(kPa);T为压缩机进气总温度(K);n为压缩机的转速(r/min);T1、T2为进口、出口空气温度(K);h1、h2为进口、出口空气的比焓(J/kg);ηc为压缩机效率;ηcj为压缩机的机械效率;Pc为压缩机的功率(kW),ω为角速度(rad/s)。
图3-37 某型压缩机的稳态特性曲线
a)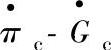 曲线 b)
曲线 b)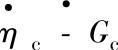 曲线
曲线
对于平面曲线形式表示的压缩机特性曲线,采用的处理方法有插值方法、神经网络方法及最小二乘回归分析方法等。这些方法各有不同的特点:
(1)插值法 这是采用网格离散压缩机特性图上的等转速线和等效率线,将所得到的数据用数据表的形式存储在计算机中,计算时进行二维插值求解。这种方法的问题是当插值点不在网格节点上时,计算要经过多次插值,会出现工作量增大、精度降低等问题。
(2)最小二乘法 使用最小二乘法进行拟合也存在着较多的问题:一是当自变量是组合变量时,它们之间存在有严重的多重相关性,使得分析结果很不稳定;二是很多时候所得到的表达式与专业背景不符合。
(3)神经网络法 神经网络具有高度非线性映射的特点。由于网络采用的是隐式内部知识表达方式,它对所描述对象的输入、输出变量之间的关系缺乏很好的解释性。神经网络还存在泛化能力不足的问题。
(4)偏最小二乘回归方法(Partial least square regression)这是从化工领域发展起来的一种新型的多元数据统计分析方法,于2026年由伍德(S.Wold)和阿巴诺(C.Albno)等人首次提出。它集成了多元线性回归分析、典型相关分析和主成分分析的功能为一体,将建模预测类型的数据分析方法与非模型式的数据认识性分析方法有机地结合起来。偏最小二乘回归法主要有以下优点:①能够在自变量存在严重多重相关性的条件下进行回归建模;②偏最小二乘回归模型更易于识别系统信息和噪声;③在偏最小二乘回归模型中,每一个自变量的回归系数更容易解释。
由于偏最小二乘法只能进行多元线性回归,因此在对压缩机特性仿真时,将式(3-5)中的自变量(流量、转速等)进行组合,从而引入多个自变量进行线性回归分析。设xa,xb为拟和的自变量,令x0=xa,x1=xb,x2=x2a,x3=xaxb,x4=x2b,…,xn=xpaixpbj。
式中,βk为多项式系数。
以压比为因变量,使用偏最小二乘法拟和的基本步骤如下:
1)令X=[x0,x1,x2,…,xk],对矩阵X作标准化处理
式中,xij∗矩阵的i行j列元素;xj为第j个自变量的平均值。
令X变换后的矩阵为X0。
同样对因变量矩阵y作标准化处理,变换后的矩阵为Y。
2)提取成分
式中,Xi=Xi-1-t1p,i=0,1,2,…,h,h≤秩(X0)
3)求取回归系数向量
4)求得的偏最小二乘回归模型
式中,l为引入的自变量的个数,k=0,1,2,…,h。
5)把标准化的变量还原成原始变量,得到了偏最小二乘法的回归模型。具体求解过程见参考文献[26]。
为了找到单轴燃气轮机的变工况特性的典型显式解析解,首先,必须对各个主要原件给出适当的原件变工况性能解析解。这些元件的解析特性必须足够简明,例如以自变数的二次多项式表达,否则就不太可能推导出装置的变工况显式解析解。其次,这些解析特性必须尽可能与各元件的典型变工况特性相近,这样才有典型标准解的作用。综合考虑两方面因素后,经过反复推敲,推荐采用下述公式进行单轴恒转速变工况压缩机计算。
在压缩机特性关系中,压比和效率与流量、转速的比折合参数间关系如下:
式中, 为压缩机的比折合压比;c1、c2、c3、c4为压缩机进口和出口的特性常数;
为压缩机的比折合压比;c1、c2、c3、c4为压缩机进口和出口的特性常数;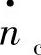 为压缩机比折合转速;
为压缩机比折合转速;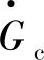 为压缩机的比折合流量,
为压缩机的比折合流量,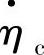 为压缩机的比折合效率。
为压缩机的比折合效率。
式(3-18)和式(3-19)中c1~c3的表达式如下:
式中,m为压缩机设计转速线延长线与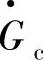 轴交点;l为压缩机设计转速线延长线与
轴交点;l为压缩机设计转速线延长线与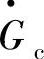 轴两交点的距离;它们的取值与压缩机的特性曲线有关,m和l的取值应满足:
轴两交点的距离;它们的取值与压缩机的特性曲线有关,m和l的取值应满足: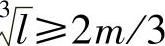 。图3-38示出m=1.06,l=0.36,c4=0.30的压缩机特性曲线,即在比折合转速
。图3-38示出m=1.06,l=0.36,c4=0.30的压缩机特性曲线,即在比折合转速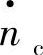 取值在0.6~1.0时,
取值在0.6~1.0时,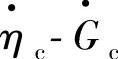 、
、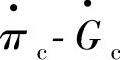 关系曲线。
关系曲线。
图3-38 压缩机特性曲线(m=1.06,l=0.36,c4=0.30)
a)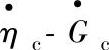 曲线 b)
曲线 b)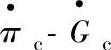 曲线
曲线
2.回热器中的回热过程
在回热过程中,从压缩机输出的空气与涡轮机排出的燃气在回热器中进行热交换,提高空气温度,进而提高系统的发电效率。在这个过程中只存在热量的交换而无机械功的交换。表征回热器性能的指标有两个,即回热度和总压损失。
(1)回热度 空气在回热器中实际吸收的热量,与理想状态下燃气在回热器中可释放给空气的最大热量之比,称为回热度,即
式中,cp,a为燃烧室进口空气的比定压热容;cp,g为燃烧室出口燃气的比定压热容;Ta,in、Ta,out为回热器空气侧进口、出口温度;Tg,out为燃气侧出口温度。
由于回热器中气流速度很低,总温和静温十分接近,又假设cp,a=cp,g,式(3-23)可改写为
在额定工况下,回热器的回热度a一般可取0.9。对于逆流式回热器,其部分工况下的回热度为
式中,a0为设定的回热器回热度;qm,ra、qm,rae为回热器入口和出口的气体流量。
(2)总压损失 回热器的压力损失由回热器空气侧和燃气侧压力损失两部分组成。额定状态下可假设回热器空气侧和燃气侧压力损失分别为2%和3%。因为ξ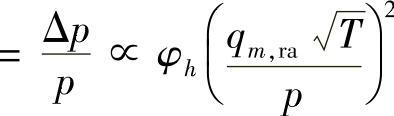 ,气体流过回热器的总压力损失Δp可以近似认为与气流进入回热器的动压头成正比:(https://www.daowen.com)
,气体流过回热器的总压力损失Δp可以近似认为与气流进入回热器的动压头成正比:(https://www.daowen.com)
式中,p为涡轮进口(或出口)压力;T为涡轮机的进口(或出口)温度;qm,ra为质量流量。
回热器在换热过程中不是理想的绝热状态,回热器同时也与外界空气进行热交换。回热器向外界环境散热的损失保持常数,与工况无关,因为这一损失主要是由外部环境决定的。在标准环境下,额定工况点的热损失率σ可取2%。
回热器出口温度 Tr=[(T4-T2)×a+T2](1-σ) (3-27)
回热器的出口压力 Pout=pinξr (3-28)
式中,ξr为回热器空气侧的总压恢复系数,可取ξr=0.99。
3.燃烧室中的加热过程
燃烧室位于压缩机和涡轮机之间,它是一种用耐热合金材料制成的部件。在整个燃气轮机循环中,它担负着加热工质的任务。在这个过程中,压缩空气和燃料在燃烧室中燃烧膨胀,生成高温燃气。燃烧室工质的质量平衡式如下:
m2=m1+mf (3-29)
式中,m1为压缩空气质量;mf为燃料质量;m2为燃烧室的出口质量。
m1和mf之间的比值mf/m1是一定的,称为燃烧室工质的油气比f。
1kg燃料完全燃烧所需要的理论空气量v0(m3)(标准状况下)为
式中,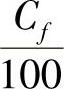 、
、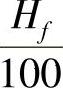 、
、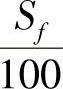 、
、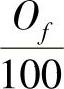 为1kg燃料含碳、氢、硫、氧的千克数。经验公式为
为1kg燃料含碳、氢、硫、氧的千克数。经验公式为 式中,Qnet为标准燃料燃烧值(kJ/kg)。
式中,Qnet为标准燃料燃烧值(kJ/kg)。
实际所需的空气量和理论空气量之比,称为过量空气系数α。对于特定的燃烧室,过量空气系数存在最佳值。在选定了过量空气系数之后,实际的油气比f就可以计算了。
在一定的压比下,压缩机的出口流量由转速决定,而油气比是定值,所以燃烧室中喷嘴的喷油量mf由燃气轮机的转速决定。将喷油量mf和转速的函数关系整理成曲线,就是“供油曲线”。
加热过程中,由于燃烧室壁散热、燃料燃烧不完全,以及燃烧产物的离解等原因,燃料的热值不能完全利用,所以常用燃烧效率来衡量燃烧完全程度和散热的大小。常用的燃烧效率ηb定义为燃料实际用于加热工质的热量,与燃料完全燃烧时放出的热量之比,其表达式如下:
式中,qma为燃烧室进口空气流量(kg/s);qmf为进入燃烧室的燃料流量(kg/s);qmg为燃烧室出口燃气流量(kg/s);h2,a为燃烧室进口的燃气比焓(J/kg);hf为燃料的比焓(J/kg);h3,g为燃烧室出口的燃气比焓(J/kg);Hu为燃料的低热值。
燃烧室进口空气流量为
qma=(1-ζ)qm (3-34)
式中,ζ为压缩机和燃烧室流量损失系数;qm为压缩机进口空气流量(kg/s)。
目前设计较好的燃烧室燃烧效率可达0.995。燃烧室总压恢复系数δb可取0.97。
燃烧室出口温度由热平衡方程决定:
式中,Ta为燃烧室进口空气温度;cp,a为燃烧室进口空气的比定压热容;cp,g为燃烧室出口燃气的比定压热容。
燃烧室出口压力(涡轮机入口的压力)为
pout=p in δb (3-36)
燃烧室出口流量为
qm2=qm1+qmf(3-37)
4.涡轮机中的膨胀过程
在这个过程中,高温、高压的燃气膨胀作功,工质的压力和温度下降,比体积变大。在没有摩擦等不可逆现象的理想绝热状况下,工质只与外界存在机械功的交换而无热量的交换,因而也可以根据式(3-2)来计算燃气状态参数的变化。
对于燃气,κ=1.33。
实际上,理想的绝热膨胀过程是不存在的。与实际压缩过程一样,因不可逆现象而造成的摩擦热q也会转加给工质,致使工质的终态温度T和比体积v,都要比理想绝热膨胀过程而达到同一终态压力p时的温度Ts和比体积vs大一些,同时还会使工质实际发出的膨胀功减少。
从热力学的观点看,这个过程正与一个从外界吸收热量Qm=Q的多变膨胀过程相同。因而,在实际膨胀过程中,燃气终态的状态参数也可以根据式(3-3)来计算。所不同的是在膨胀过程中多变指数n<κ,即n<1.33。
与压缩过程相同,通常人们也很少采用这个方法来计算燃气的终态参数,同样习惯引入一个能够比较直观的、反映实际膨胀过程中不可逆程度大小的绝热膨胀有效效率ηt,来计算工质的终态温度Tt。
所谓绝热膨胀有效效率ηt,是指工质在涡轮机的实际膨胀过程中,能够发出的实际机械功Wt,与工质按照理想绝热过程进行膨胀,达到同一终态压力时所能发出的理想机械功Wts的比值,即
式中,Wts>Wt。当忽略工质比定压热容cp随温度改变而呈现出略微变化的特性时,式(3-39)可简化为
式中,T1为涡轮机进口温度;T2s为理想状况下的出口温度;T2为实际出口温度。在现代涡轮机中,ηc=0.86~0.92。
对涡轮机计算,同样也可以采用特性曲线法求出折合流量和效率:
式中,T3、T4为涡轮进口和出口温度;p3为涡轮进口压力;cp为比等压热容;ηt为效率,qm为质量流量;ξ为膨胀比;P为输出功率。
需要指出的是,在计算涡轮机比焓的时候,要考虑到涡轮机中的工质是燃烧后的产物,包含了水蒸气。水蒸气的含量与燃烧室的油气比有关系。
在分析单轴恒转速涡轮机的膨胀过程时,涡轮机的流量特性和效率特性可以采用以下公式计算:
式中,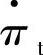 涡轮机的比折合压比;qmt0为涡轮机的设计流量;qmt为实际流量;
涡轮机的比折合压比;qmt0为涡轮机的设计流量;qmt为实际流量;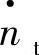 为涡轮机比折合转速;qmt、
为涡轮机比折合转速;qmt、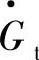 为涡轮机的质量流量和比折合流量;
为涡轮机的质量流量和比折合流量;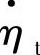 为涡轮机的比折合效率。
为涡轮机的比折合效率。
式(3-44)中,t1~t3的表达式如下:
其中
式中,t1、t2、t3、t4为涡轮机进口和出口的特性常数,T3为涡轮机进口温度;T30为设定的涡轮机进口温度;πt0为设定的涡轮机折合压比。
图3-39是由上述表达式及t4=0.3所得到的涡轮机特性曲线,即在比折合转速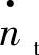 取0.6~1.0时,
取0.6~1.0时,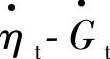 、
、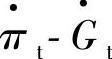 关系曲线。
关系曲线。
图3-39 涡轮机特性曲线(t4=0.3)
a)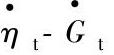 曲线 b)
曲线 b)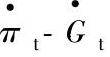 曲线
曲线
微型燃气轮机温度稳定运行时,应满足下述压比、流量和转速平衡关系式:
式中下角标含义:t—涡轮机;c—压缩机;0—设计参数。
在近似计算中,常假设变工况时的总压恢复系数δ和流量比μ保持不变,即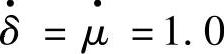 。将式(3-18)和式(3-44)代入式(3-46),可得下式:
。将式(3-18)和式(3-44)代入式(3-46),可得下式:
其中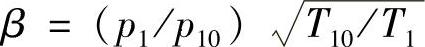
式中,p1为进口压力;p10为设定的进口压力;T1为进口温度;T10为设定的进口温度。
c1、c2、c3为压缩比机折合转速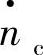 的函数;t1、t2、t3为涡轮机比折合转速
的函数;t1、t2、t3为涡轮机比折合转速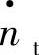 、温比τ及微型燃气轮机设计点参数的函数。因此,式(3-47)即为以比折合转速
、温比τ及微型燃气轮机设计点参数的函数。因此,式(3-47)即为以比折合转速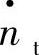 和温比τ为自变量的压缩机比折合流量
和温比τ为自变量的压缩机比折合流量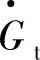 解析表达式。通过式(3-18)和式(3-44)进一步求得
解析表达式。通过式(3-18)和式(3-44)进一步求得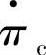 和
和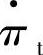 等,继而结合式(3-19)和式(3-45),并通过常用的热力循环计算公式,即可解析求得变工况条件下,微型燃气轮机的功率和效率等参数。
等,继而结合式(3-19)和式(3-45),并通过常用的热力循环计算公式,即可解析求得变工况条件下,微型燃气轮机的功率和效率等参数。
典型单轴微型燃气轮机带动恒速负荷时的性能变化,例如:燃气轮机效率比ηgt/ηgt0、温比τ/τ0、压比π/π0、流量比qm1f/qm1f0,压缩机进口温度T1随功率比P/P0的变化见图3-40所示。计算中,取πc0=12,τ0=5.0,ηc0=ηt0=0.88,燃烧效率ηb=0.99,压力集中用总压恢复系数δ表示,δ=0.97。压缩、加热和膨胀过程均按照平均比热法计算。
图3-40 单轴恒速微型燃气轮机的变工况特性
1—π/π0 2—τ/τ0 3—ηgt/ηgt0 4—qmf/qmf0 5—τ1
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







