编码是通信理论系统中非常重要乃至核心的理论和技术，从广义的角度来讲包括调制在内的各种信息处理手段都可以当作有限域到实数域的一个编码方案。香农在其开创性的信息理论中深化了人们对于通信系统的认识，将通信在工程上的信息传输过程数学建模化到了从一个可能的集合中选择、估计相关发送信息的一个概率问题上来，而处于中心的两个重要问题就是有效性和可靠性。狭义的信息论与编码理论中的信源编码和信道编码就是人们对解决这两个问题的一个积极的尝试，经过60多年的不懈努力，人们在各个方面都取得了很大的突破。

在香农之前人们一直认为信息的有效性和可靠性是不可兼得的，增加可靠性意味着更多的冗余位，而这又势必会降低有效性，在足够可靠的情况下信息的有效性可能会趋于0。而实际上只要信息传输速率不超过对应信道的信道容量，就可以保证传输的差错概率任意小。信源可以看作一系列的随机序列{X_n}，香农证明存在一个被称为信息熵的H(X)，只要R＞H(X)，就可以使用R比特对信源进行编码并无损地恢复。而对于信道，一般是一个以一定转移概率W（y丨x）的映射W：X→Y，如前面所说，对于R＜H(X)的信息可以实现可靠的传输。把信源和信道联合起来考虑，基于信源信道编码分离定理，可知在H(X)＜(X)的情况下可以实现无失真的可靠传输。在离散无记忆时，联合的信源信道编码和分离情况下的性能在渐进下是没有性能上的区别的：但在有限长度实际方案情况下，考虑效率与复杂度等问题，以及有记忆信道条件下，联合的编码还是有一些潜在的好处的。当H(X)＞(X)时，不能保证无损的可靠传输，但可以在信道一致下尽量降低信源编码的译码失真度。假设R(D)为限失真函数的门限，当R(D)＜C（W）时，就可以在满足失真度不大于D的前提下实现可靠传输。

最开始出现的编码是代数方法的编码，更准确地说是F₂域内的线性分组码。在香农的证明中，渐进性能下足够长的码在平均意义下可以达到任意小的差错性能，随机编码的码书往往都是较优的码，在这种任意映射下需要的存储空间会高达O(N2^NR)，这在N较大时是难以接受的。进一步，Elias等人证明在重要的一大类信道中，线性码可以达到信道容量。线性码可以看作是线性空间的一个子空间，只需要对维度N的NR个基进行存储就可以实现编码，因而总的存储空间为O(N²)，和随机码书相比在空间复杂度方面可获得非常大的改进。这时一般采用硬判决的译码方案，在信道容量上和软判决相比有约2 dB的损失。汉明距离是衡量性能的一个重要指标，线性编码中成对差错概率的计算和最小汉明距离有很大的关系，通常用（n，k，d）表示编码长度n，信息长度k，最小汉明距d的码。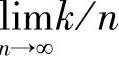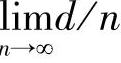当中有很多码字性能的界限如外界的汉明界、普洛特金界等，以及V-G内界，然而遗憾的是，在固定时，往往趋近0，和相应的界限相差较大。在这一时期，学术界发现了球包界下完备的Hamming码，有严谨有限域数学基础的BCH、RS码等，Reed-Muller码，以及CRC检错检验码等。Elias提出的乘积码和Forney提出的级联码都是在代数域编码体制下的一种有效的性能增强方案，以希望通过短码的译码复杂度来达到近似长码的差错性能。

在代数译码之后一个重大的突破就是概率译码算法的使用，在高斯信道下软信息的利用能够获得比硬判决更大的信道容量，而概率译码比较典型的应用就是Elias提出的卷积码。不同于分组码译码复杂度与码长有关，卷积码中重要的是其寄存器状态的数量，其差错概率性能也主要由自由距离所决定。业界提出了多种卷积码译码算法如大数逻辑、代数译码、堆栈译码等；Viterbi提出的Viterbi译码算法可以在线性复杂度下达到码字最优；BCJR算法是达到比特最大后验的最优算法，BCJR也是在Turbo码中比较常用的译码算法。除在功率受限信道上的信道编码之外，在带宽受限信道上的网格编码调制和多级编码等思想，将有限域内对码字汉明距离的衡量转换到了欧式距离下的讨论，子集划分等联合编码和调制的优化，对带宽受限信道下的高阶调制是一个很有效的方法。

Berrou等人Turbo码的发明是现代编码理论的重大突破，它改变了人们对经典编码理论的认识。Turbo码的性能突破了信道截止速率，这个速率在此之前一直被人们认为是可实现复杂度下编码的实际极限界。香农界是一个理论性能界，在信道截止速率之下的高复杂度卷积码，也可以通过堆栈或Fano译码等算法降低复杂度；而对于高过这一截止速率的卷积码，虽然Fano等算法依然有效，但复杂度无法保证，译码时堆栈可能会不断地进出形成震荡。Turbo码的结构是通过交织器将两个卷积码并行级联起来，并采用迭代译码的算法来逼近最大似然准则：交织级联使得Turbo码有大的约束距离，这也是香农理论中一个好码应该具备的性质；而迭代译码算法的应用使得Turbo码的译码性能尽量收敛到最大似然界上来。自此之后，Turbo迭代译码原理在各个领域有着广泛的应用。现代编码理论另一个重大突破是Gallager在20世纪60年代提出的LDPC码的再发现，LDPC码中使用的因子图、置信传播算法等思想也成为了现代编码理论中的核心理论。Wiberg等人将Turbo码和LDPC码统一到了在图上的编码，MacKay和Neal提出在这之上的置信传播算法也和机器学习、计算机科学等领域有着内在的联系。将密度进化、置信传播算法等进行最优化，目前已经可构建出在高斯信道下和香农限相差仅0.0045dB的编码，而且许多新的LDPC码或其他编码方案也在不断构建。

·信道极化码(www.daowen.com)

Arikan在2009年提出的信道极化码^[22]是信道编码理论的重大突破，从理论上可证明其能通过O（NlogN）的编译码复杂度达到离散对称信道的信道容量，并且差错概率上界为O（N^-1/4）。极化码通过递归的构建方式和串行干扰抵消译码算法，将独立的N个信道变换成2类：一类是互信息很大的信道，在此信道可以传递不用编码的信息；另一类是互信息很小的信道，在此信道无法传递信息，如图7-35所示。可以看到，互信息大的信道比例正好是信道容量。

·OVTDM（Overlapped Time-Domain Multiplexing）

传统的编码利用电平分割奈奎斯特采样的方式进行，以确保信号的无符号干扰。OVT-DM技术指出：系统内部数据符号间的相互重叠不是干扰，是自然形成的编码约束关系，且重叠越严重编码增益越高。因而，利用重叠复用，即通过数据加权复用波形移位重叠，形成了一种高频谱效率的新型编码方式。

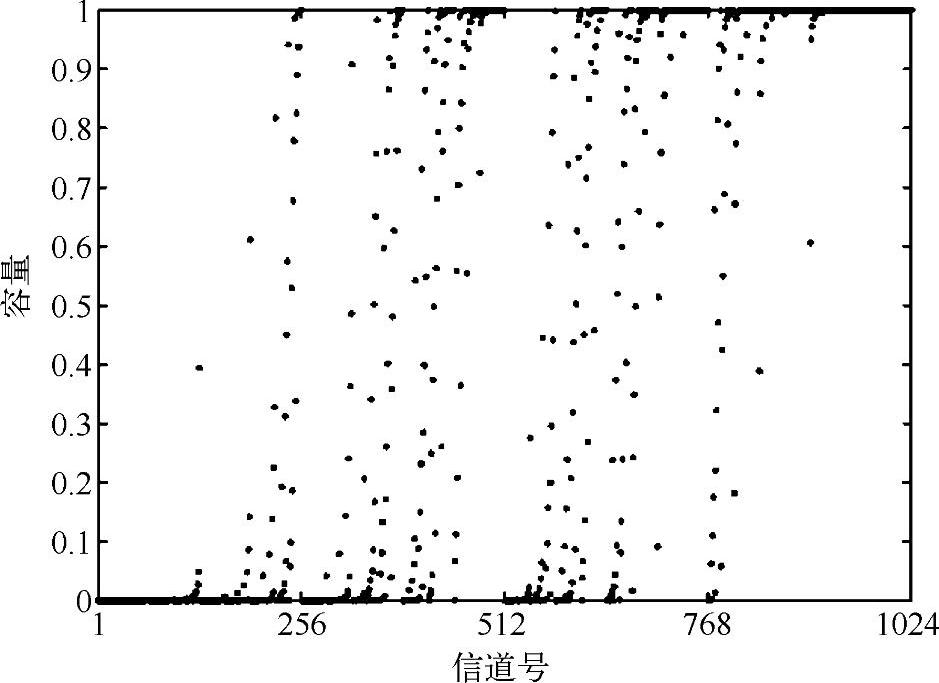
图7-35 信道极化等效信道互信息[22]