由于通信系统的非对称性，上、下行系统模型存在显著差别。上行通信系统是多点发送、单点接收，单用户功率受限，同时发送的用户越多则总发送功率越高，发送端难以联合处理而接收端可以联合处理，相应的模型称为多接入信道。下行通信是单点发送、多点接收，总发送功率受限，同时接收的用户越多则分给单用户的功率越少，发送端可以联合处理而接收端难以联合处理，相应的模型称为广播信道。由于系统模型和特点不同，上、下行信道的容量和最优传输策略也不相同。本节将对上、下行信道容量分别进行分析^[3]。

1.上行多接入信道

上行高斯多接入信道的模型可以表示为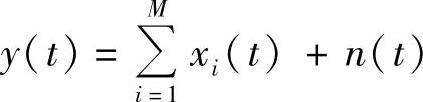。其中，x_i（t）为信源Ui（i=1，…，M）编码后的发送信号，满足E[x_i²（t）]≤P_i的功率约束，且多用户占用相同的带宽W；n（t）为加性高斯白噪声，其双边功率谱密度为N₀/2；y（t）为接收信号。高斯多接入信道的容量是已知的，表示为^[3]：

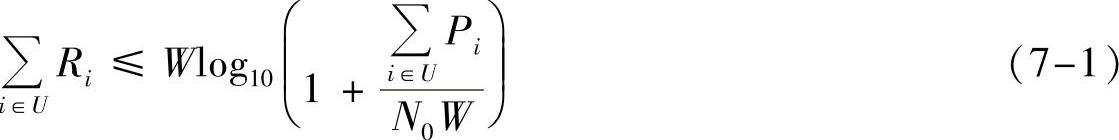
其中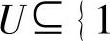，，…，M}。

以2个用户为例，基于式（7-1）可得到高斯多接入信道的容量，如图7-7中的折线所示。除明确上行多接入信道的容量界之外，达到容量的发送和接收策略也十分重要。在发送端，2个用户在相同的资源上各自发送随机编码后的调制信息，并在空口进行直接叠加。在接收端，为了达到图7-7中A、B两拐点的容量，可以采用SIC（Successive Interference Cancellation，串行干扰删除）接收机，即：先将用户1（或用户2）的符号当作干扰，译码用户2（或用户1）的符号；然后删除用户2（或用户1）的符号，再译码用户1（或用户2）的符号。然而基于SIC的策略不能直接达到线段AB（不包含A点和B点）上的容量。若要达到线段AB上的容量，可通过在A点和B点间的正交复用方式来实现，或者在接收端采用多用户联合最大似然译码。

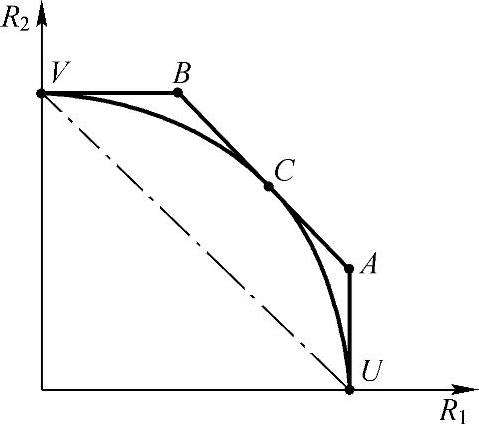
图7-7 两用户的多接入信道容量界

图7-7中的U点和V点分别代表用户1和用户2独占所有资源时的信道容量。对于时分多址正交系统，假设2个用户在T时间内分别占用T₁、T₂的时间传输，且在各自传输的时间里满足E[x_i²（t）]≤P_i的功率约束，则信道容量为：

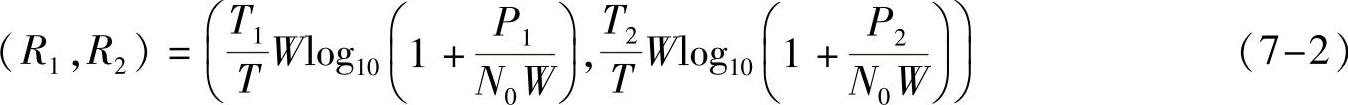
对于频分多址正交系统，假设2个用户各占用的带宽为W₁、W₂，且2个用户在各自频带内的信号功率谱密度与单用户独占带宽W时相同，则信道容量为：

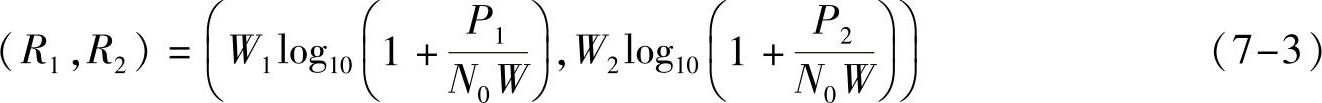
在此约束下，时分和频分多址正交的容量均为图7-7中的虚线所示。

进一步，考虑借功率场景下的正交多址系统，即在时分多址时将功率约束放宽为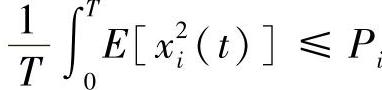，则用户i在传输时间T_i内，功率可提升至E[x²_i（t）]≤P_iT/T_i，（∀t∈T_i）；类似地，在频分多址中，允许用户i在带宽W_i内发射全部的功率。这时时分多址和频分多址的容量分别为：

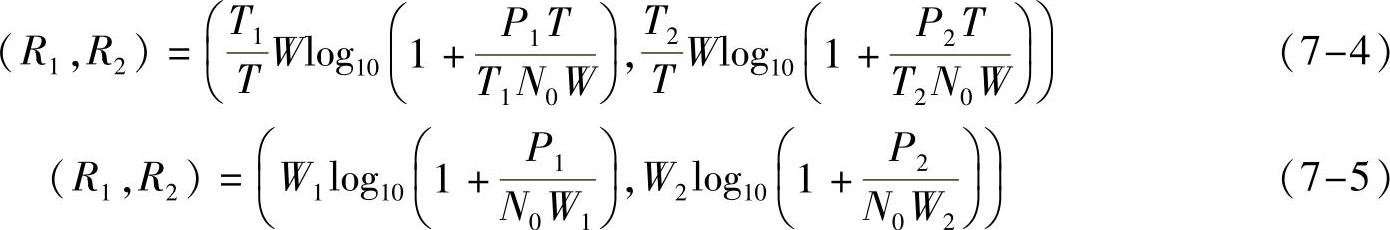(www.daowen.com)

可以看到，借功率场景下，时分和频分正交多址的容量均为图7-7中的弧线所示^[2]。可借功率的正交多址系统可以在C点达到多接入信道的和容量。然而，当2个用户的功率不对等时（即存在远近效应），如图7-8所示，虽然可借功率正交接入的C点和容量与多接入信道的A点和容量相等，然而C点所对应的R₁＜＜R₂，用户间公平性较差。

4G LTE采用正交多址接入，而且考虑实际系统和小区间干扰等因素，上行不采用借功率方案^[4]，因而仅能达到图7-7中虚线所表示的信道容量。若在5G系统中引入非正交多址接入，理论上将有显著的频谱效率提升空间。另一方面，虽然从上行多接入信道的角度，最优的发送策略是所有用户同时满功率发送。然而，实际的蜂窝通信系统是个复杂的干扰信道，且干扰不能完全消除，更多用户的同时发送将给邻小区带来无法完全消除的干扰。因此，对于较多用户同时发送时的实际性能，还需考虑系统设计和工程约束，并进行全面的评估与优化。

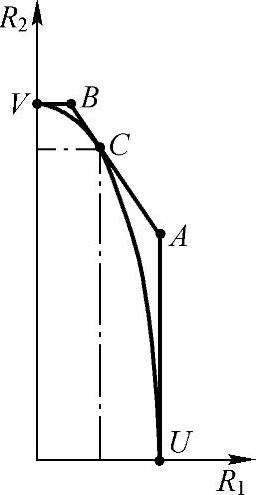
图7-8 功率不对等时的两用户多接入信道容量界

2.下行广播信道

下行高斯广播信道的模型可表示为y_i（t）=x（t）+n_i（t）（i=1，…，M）。其中，x（t）为M个信源U_i联合编码后的发送信号，满足E[x²（t）]≤P的功率约束，带宽为W；n_i（t）为第i个用户的加性高斯白噪声，其双边功率谱密度为N_i/2；y_i（t）为第i个用户的接收信号。高斯广播信道中，多用户的信道质量可以排序，不失一般性假设N₁≤…N_j≤…N_i≤…N_M。因此，若一个用户i可以正确译码自身的信息，则信道质量优于用户i的其他任意用户j也能正确译码用户i的信息。因此，高斯广播信道是一种退化广播信道，其容量是已知的，可表示为^[2]：

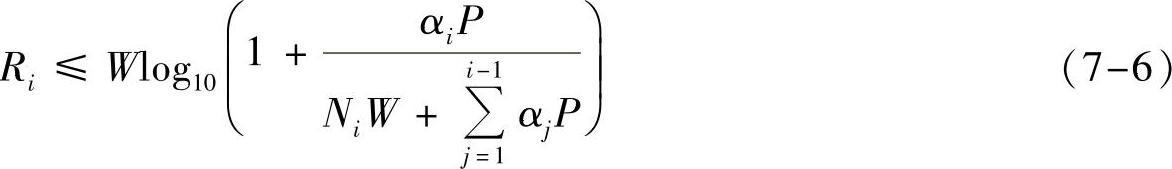
其中，α_i是分配给用户i的功率比例，满足

。

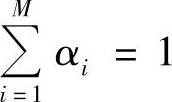对于一般的退化广播信道，可以采用叠加编码（Superposition Code）达到信道容量。而对于高斯广播信道，可通过发送端信号的直接叠加和接收端的串行干扰删除接收机，来达到信道容量，具体地：给任意用户i分配一定的功率α_iP；在译码时，将信道质量好于用户i的用户j（N_j＜N_i）信息当作干扰，同时将信道质量差于用户i的用户k（N_k＞N_i）信息译码并删除。

以2个用户为例，考虑不同的功率分配因子，基于式（7-6）可得到高斯广播信道的容量，如图7-9中的实线所示。下行正交多址的容量与上行正交多址的容量类似，如图7-7的点画线所示。由于下行多用户的总功率受限，因此没有借功率的场景。

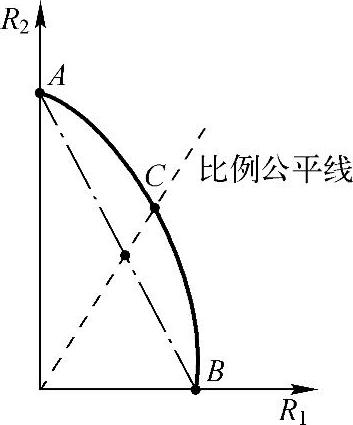
图7-9 两用户的广播信道容量界

通过容量表达式（7-6）可以看到，首先，如果没有远近效应，也就是所有用户的噪声方差相同，则下行高斯广播信道下，非正交多址的容量与正交多址的容量相同。其次，如果追求和容量最大的准则，则最优的策略是将所有功率分配给信道质量最好的用户，即图7-9中的A点。因此，在存在远近效应，且考虑多用户公平性的实际场景中，非正交多址的理论容量优于正交多址，且能达到高斯广播容量限。