【摘要】:在用球头立铣刀铣削曲面时,球头刀的切削刃面上一点与曲面始终处于相切,而此时球头刀上切削平面上的切削刃半径≤球头刀名义半径。同理,由刀具切削进给速度计算公式F=n×fz×z可知,进给速度与主轴转速是成正比的,它随着主轴转速的增大而增大。
在用球头立铣刀铣削曲面时,球头刀的切削刃面上一点与曲面始终处于相切,而此时球头刀上切削平面上的切削刃半径≤球头刀名义半径。因此,我们在计算主轴转速时,此时的刀具半径不应该是球头刀的名义半径,而应是实际球头刀切削刃处的球面半径,如图5-18中的R1、R2、R3所示。
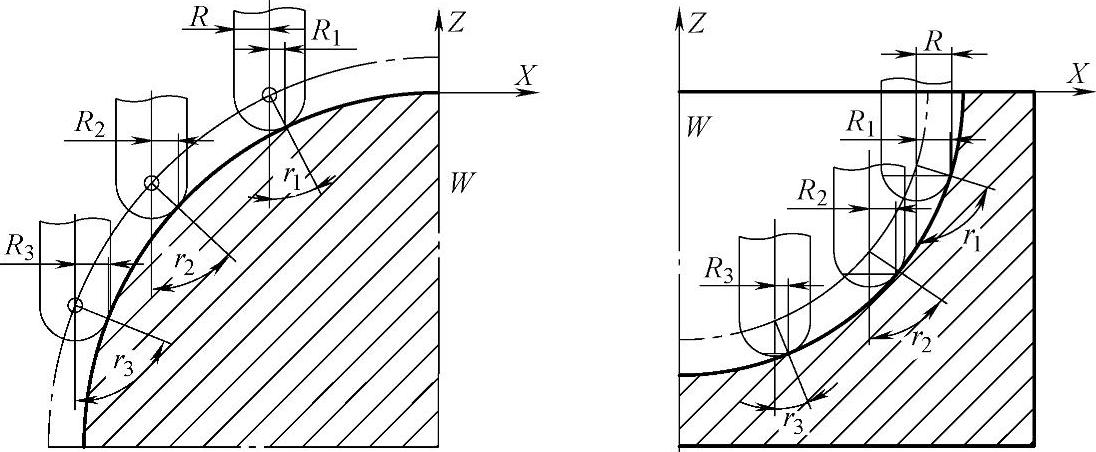
图5-18 球面上各点处的实际切削半径
根据切削用量的主轴转速计算公式:
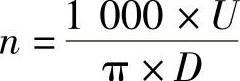
;
进给速度计算公式:
F=n×fz×z;
式中 n——主轴转速,r/min;
U——精加工切削速度,m/min;
D——刀具名义直径,mm;
F——刀具进给速度,mm/min;
fz——刀具每齿进给量,mm/齿;
z——刀具齿数。(www.daowen.com)
此时公式中的刀具直径(D)是个变量,它随着刀具切削刃处与刀心的连线与刀具轴线的角度的变化而变化,如图5-18中的r1、r2、r3;又因为主轴的转速与刀具的直径是成反比的,所以球头铣刀在切削曲面时,球面上各点处的主轴转速都要比球头刀周齿上的转速高。同理,由刀具切削进给速度计算公式F=n×fz×z可知,进给速度与主轴转速是成正比的,它随着主轴转速的增大而增大。
由图5-18可计算出切削刃处的半径值:
R1,2,3…=R×cosr1,2,3,…
例题5-9:用ϕ10mm高速钢球头铣刀精铣如图5-19所示的凹半球曲面。求出球面上各点处的切削速度
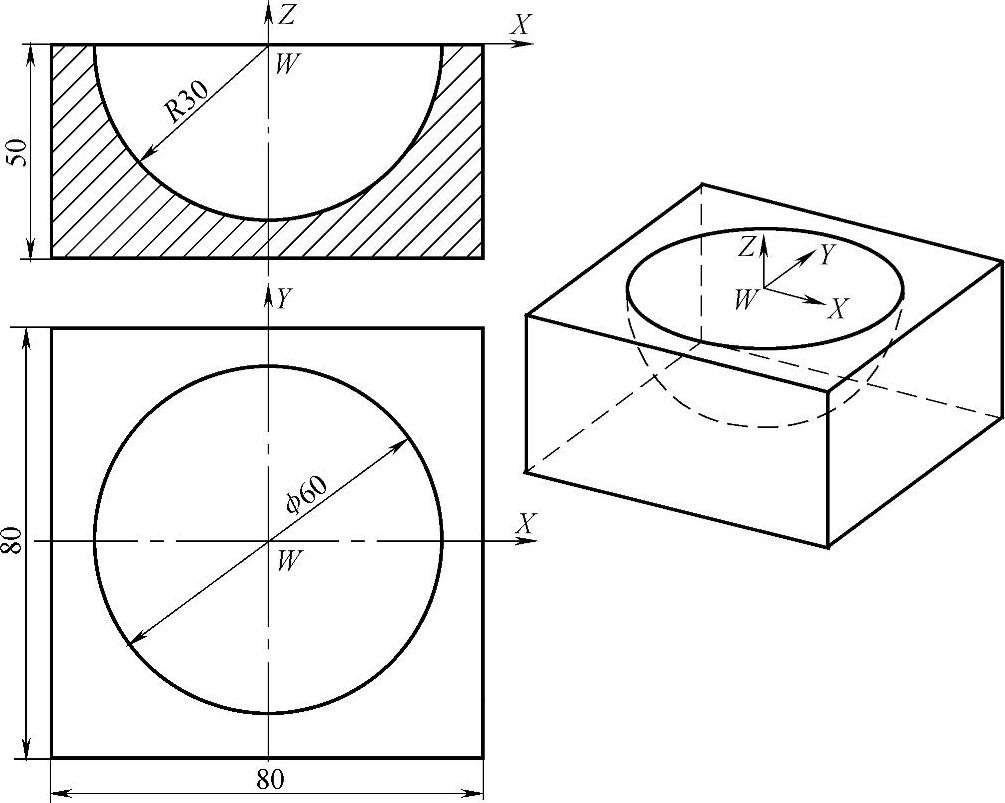
图5-19 球凹半球各点处切削速度例题
解:假设,我们取切削速度(V)为40m/min,每齿进给量为0.1mm,则主轴转速应为
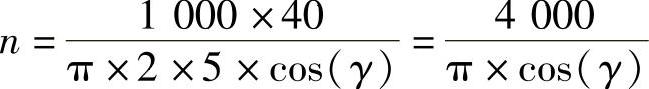
;
程序编制如下:(FANUC 0i数控系统)


免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关数控编程疑难解答的文章







