由上图5-9a、b可知,图中1至3处的坐标值递增(递减)量可用表达式计算。
(1)球头铣刀
水平方向(X或Y):1s=0
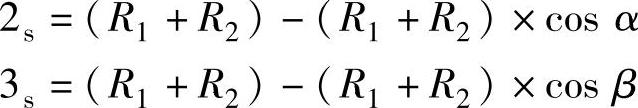
垂直方向(Z):1c=0
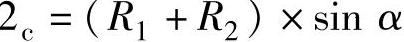
3c=(R1+R2)×sinβ
(2)平底铣刀
水平方向(X或Y):1s=0

垂直方向(Z):1c=0
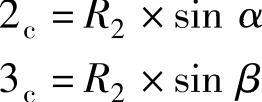
R1为球刀的半径,R2为球面半径,α、β为球刀的球心与球面球心的连线与水平轴的角度,假设角度的递增(递减)为等值递增(递减),每次递增(递减)5°,则半球面被等分成18份;用变量1表示球面上水平方向上从0~90°的角度,每次递增(递减)5°,则:
水平方向上的刀心坐标为(R1+R2)×cos[1];
垂直方向上的刀心坐标为(R1+R2)×sin[1]。
刀具半径补偿递减值为(https://www.daowen.com)
ΔR=(R1+R2)-(R1+R2)×cos[1],刀具半径补偿值就等于球刀半径-刀具半径补偿递减值。
即R1-ΔR;它随着自变量1角度的变化而变化。
图5-9c和图5-9d中,在三角形中,C1/C2=tanβ为一个常量,用变量2表示三角形斜面上各点的高度,并将它们等分成n段,用2=ΔZ=(C2+R/sinβ/n作为Z轴上高度的递增均值(自变量)。
则:水平方向的变化均值为ΔX(ΔY)=2×tanβ;即为刀具半径补偿值的递增值。
从上述可知,在进行非圆曲线或不规则内轮廓倒圆或倒角时,我们常采用刀具半径的递增(递减)变化来加工,在加工内、外轮廓时,当刀具从下往上倒凸圆弧时,刀具半径逐渐减小,当刀具从上往下倒凸圆弧时,刀具半径逐渐增大。
刀具半径是一个变量,而我们在加工工件时,刀具半径通常作为一个常量,被输入到系统的刀具存储器中,作为系统变量被存储;系统变量在程序中是不可改变的,而此时刀具半径是一个变量,如还是作为系统变量来频繁地更改输入是不可取的,因此,这里将刀具半径值作为为全局变量,使刀具半径随着程序中自变量的递增(递减)而递增(递减)。
例题5-5:根据图5-10中零件所示,编写大凸台的轮廓周边倒R5mm圆弧程序和ϕ40mm圆槽孔口倒120°角程序;刀具为R4mm高速钢球头铣刀。
解:由图5-10所示,大凸台是由R35mm、R65mm、R25mm圆弧和直线组成的不规则轮廓,轮廓上表面与侧面均匀倒R5mm圆角;在凸台轮廓加工好后,刀具下降至凸台轮廓上表面下5mm处,通过刀具的周齿开始由下往上对轮廓有规律的进行缩放加工,将刀具半径作为自变量,高度作为应变量进行程序设计。同理,ϕ40mm圆槽孔口倒角也是从下往上分层编程加工。

图5-10 例题5-5零件
程序编制如下:(FANUC 0i数控系统大凸台轮廓倒圆弧和ϕ40mm圆槽孔口倒120°例角程序)



免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






