如图3.1（a）所示，平面立体的各表面均为多边形，称为棱面。各棱面的交线称为棱线。棱线与棱线的交点称为顶点。求作平面立体的投影，就是作出组成平面立体的各表面、各棱线和各顶点的投影，由于点、线和面是构成平面立体表面的几何元素，因此，绘制平面立体的投影，归根结底是绘制直线和平面的投影。其中可见的棱线投影画成粗实线，不可见的棱线投影画成细虚线，以区分可见表面和不可见表面。当粗实线和虚线重合时，可只画粗实线。

1）棱柱

棱柱由两个相互平行的底面和若干个侧棱面围成，相邻两侧棱面的交线称为侧棱线，简称棱线。棱柱的棱线相互平行。如图3.3所示，工程中常见的棱柱有三棱柱、四棱柱、五棱柱和六棱柱等。

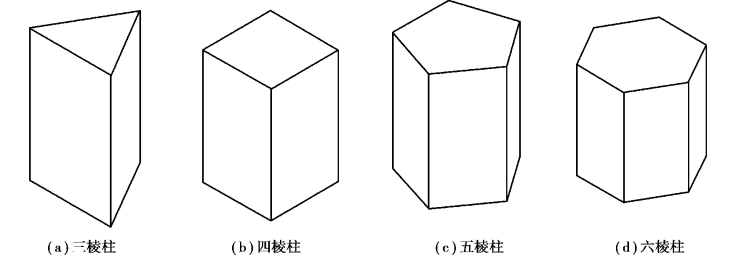
图3.3　工程中常见的棱柱

（1）棱柱的三视图

以正六棱柱为例，如图3.4（a）所示是正六棱柱的立体图，它是由上下两个正六边形底面和6个四边形的棱面构成。选择六棱柱的主视方向时，需要考虑两个因素：一是要使得六棱柱处于稳定状态；二是要考虑六棱柱的工作状态。为了作图方便，应尽量使六棱柱的表面平行或垂直投影面。

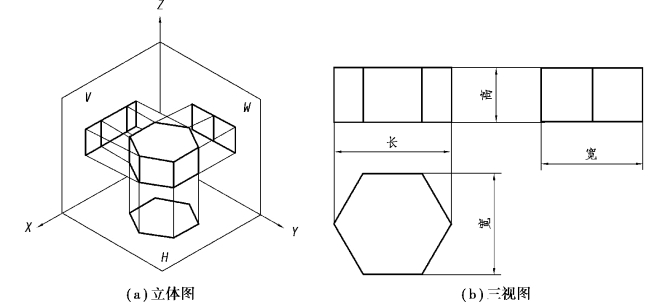
图3.4　正六棱柱的三视图

如图3.4（b）所示，从正六棱柱的三视图可以看到其俯视图是一个正六边形，它是正六棱柱上下底面的投影，正六边形的6条边分别是6个棱面的积聚性投影，正六边形的6个顶点分别是正六棱柱的6条棱线的水平面投影，它反映了投影的积聚性。主视图中3个并立的矩形是正六棱柱左、中和右3个棱面的投影，主视图的外形轮廓分别是正六棱柱上、下底面和左、右棱线的投影。左视图的两个并列的矩形是正六棱柱左、右4个棱面的重叠投影，上下两条水平线是正六棱柱上下底面的积聚性投影，前后两条投影垂直线分别是正六棱柱前后棱面的积聚性投影，中间的垂直投影线则是正六棱柱左右两条棱线的重叠投影。

（2）棱柱表面上求点

棱柱表面上求点可以利用柱体表面的积聚性投影来作图。立体表面上的点一般用大写字母表示，如M。主视图上立体表面上的点一般用小写字母加一撇表示，如m′。俯视图上立体表面上的点一般用小写字母表示，如m。左视图上立体表面上的点一般用小写字母加两撇表示，如m″。

如图3.5所示，已知正五棱柱的三视图及其表面ABCD上点M的主视图上点投影m′，求作它的另两个投影m和m″。

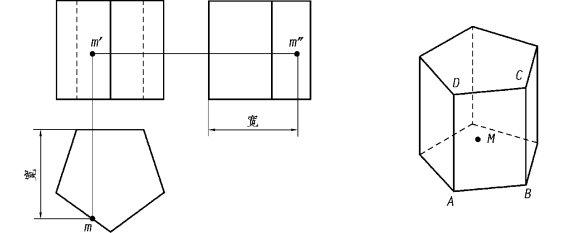
图3.5　正五棱柱表面上求点(www.daowen.com)

根据已知条件，同时依据点M的主视图投影点m′的可见性条件，推断出M点必在五棱柱前面的棱面上。利用棱柱各棱面的俯视图具有积聚性特点，可向下作辅助线直接找到点M的俯视图投影点m，最后可按“高平齐、宽相等”的投影规律求出点的左视图投影点m″。

2）棱锥

棱锥由一个底面和若干个三角形侧棱面围成，且所有棱面相交于一点，称为锥顶，常记为S。棱锥相邻两棱面的交线称为棱线，所有的棱线都交于锥顶S。工程中常用的棱锥包括三棱锥、四棱锥和五棱锥等。

（1）棱锥的三视图

从如图3.6所示的正三棱锥的三视图中可以看出，其俯视图是由3个全等的三角形组成的，它们分别是3个棱面的水平投影，形状为等边三角形的外形轮廓则是三棱锥底面的投影，它反映了底面的实际形状。主视图由两个三角形组成，它们是三棱锥左右三棱面的投影，而外形轮廓的等腰三角形则是后棱面的投影，其底边为三棱锥底面的投影。左视图是一个三角形，它是左右两个棱面的重叠投影，靠里侧的斜边是侧垂位置的后棱面的投影，底边仍为三棱锥底面的投影。

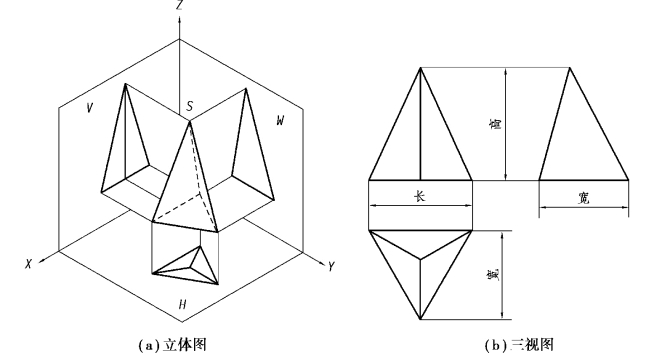
图3.6　正三棱锥的三视图

（2）棱锥表面上求点

棱锥表面上求点可以在锥体表面上过点任意作一条直线作为解题的辅助线，为了作图方便，一般这条辅助线可以绘制成过锥顶的直线或过点作平行与锥底的直线。

如图3.7所示为过锥顶作辅助线法求作三棱锥表面上的点。已知三棱锥表面上的点K在主视图上的投影k′，求作点K的俯视图的投影点k和左视图的投影点k″。首先在主视图上过锥顶作辅助线s′d′，其次利用“长对正”的投影规律求出点d和点k，最后利用“高平齐，宽相等”的投影规律求出点d″和点k″。

如图3.8所示为过点作平行锥底辅助线法求作三棱锥表面上的点。已知点K在主视图上的投影点k′，求作俯视图投影点k和左视图投影点k″。首先在主视图上作辅助线m′n′∥a′c′，接着利用“长对正”的投影规律求作点m，然后在俯视图上作mn∥ac以求作点n和点k，最后利用“高平齐，宽相等”的投影规律求作左视图上的点m″、点n″和点k″。

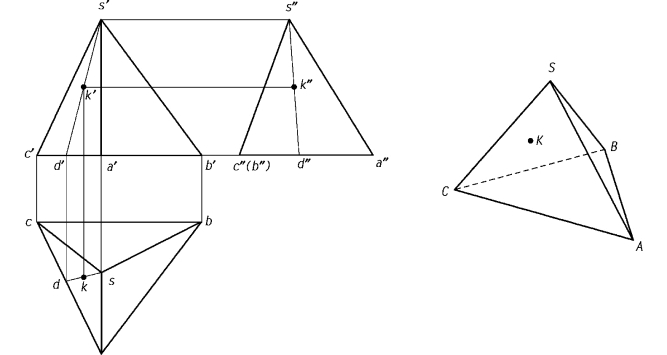
图3.7　正三棱锥表面上求点（过锥顶辅助线法）

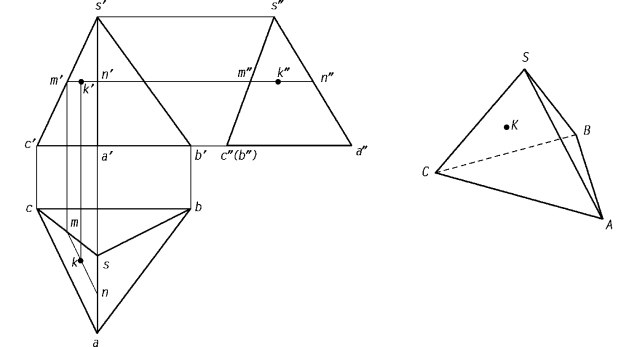
图3.8　正三棱锥表面上求点（平行锥底辅助线法）