本节结合财务会计核算准则构建引洮供水公司和自来水厂双方利益博弈模型以及欠发达地区政府补贴下的引洮供水公司和自来水厂（含农民用水者协会）的博弈模型,并通过均衡分析研究调水工程供应链中的利益分配问题以及欠发达地区调水工程供应链用水户承受力不足情况下的政府补贴问题。

（1）水资源供应链整体盈利下的博弈

1）问题描述

调水工程供应链涉及多个利益主体。引洮工程处于供应链最上游的九甸峡水电站并不对下游的引洮供水公司收取水资源费,基本上是免费供水。对末端的受水区用户而言,水价未超过其承受力时,其将持续使用工程水,否则将弃用工程水,使用其他水源。[149]在承受力水价约束的条件下,引洮供水公司和自来水厂如何进行利益分配是决定工程健康运营的决定性因素。因此主要考虑引洮供水公司和自来水厂之间的博弈问题。

价格是二者的利益纽带,引洮供水公司决定价格Pm下供水或不供水,自来水厂决定价格P 下用水或者不用水,Q 为供水量与用水量。分别用V1、V2,F1、F2,π1、π2表示引洮供水公司和自来水厂的单位变动成本、固定成本以及总利润,博弈树见图4.6。

图4.6　调水工程二级供应链博弈树

如果引洮供水公司选择不供水,则自来水厂只能选择不用水,均衡结果为（-F1,-F2）。如果引洮供水公司决定以价格Pm进行供水,则自来水厂选择用水的均衡结果为（π1,π2）,选择不用水的均衡结果为（-V1Q - F1,-F2）。收益矩阵见表4.19。

表4.19　引洮供水公司和自来水厂收益矩阵

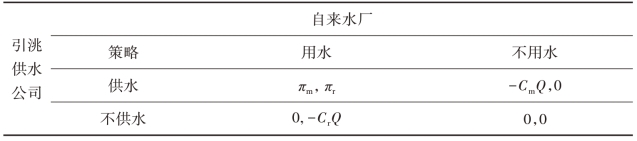
PQ ＞(V1 + V2)Q + F1 + F2 时,π1+π2=(P - V1 - V2)Q - F1 - F2 ＞0,也就是说自来水厂的水价P 足够高的情况下,如果引洮供水公司的价格Pm 确定合理,就会有π1 ＞-F1且π2 ＞-F2,双方的最优策略组合为（供水,用水）,在其他时候,双方获得的收益均更少,这是一个典型的纳什均衡。

引洮供水公司和自来水厂之间有非合作与合作两种博弈情形。非合作情形下,由于引洮供水公司处于主导者的地位,可以凭借先动优势首先确定一个有利于自己的定价,而后由自来水厂根据引洮供水公司的定价以及其他约束条件确定自己的最优报价。合作情形下,二者之间事先签订合作协议,约定风险共担、收益共享,在协作获取更大利益之后,再按照事先约定的比例进行利润分配。

本部分就自来水厂的价格足够弥补双方总成本的情况,分析二者在非合作与合作下的定价以及分配利润问题。

2）模型假设

第一,局中人包括一个供水公司和一个自来水厂,二者都是理性经济人。

第二,供水公司的策略集为｛供水,不供水｝,自来水厂的策略集为｛用水,不用水｝,决策按照供水公司→自来水厂的顺序进行。

第三,除了供水公司以外,自来水厂没有别的水源可用。

第四,自来水的需求量是零售价格的递减函数,需求函数为：

即,Q0表示市场最大需求量,α为销售量对自来水价格的敏感系数,α ＞0。Q ＞0,Q等于供水公司和自来水厂的供水量。假设供水量等于双方制水量。

3）变量说明

依照财务会计学方法核算供水公司以及自来水厂的成本费用并按照供水量分摊为单位成本费用。根据上节内容,供水公司以及自来水厂的成本费用如下：

供水公司的单位成本费用Cm=（基本折旧费用+运行费用+流动资金利息）/Q,其中,运行费用=工程维修费+工资福利费+工程管理费+动力费+其他费用。

自来水厂的单位配水成本费用Cr=（主营成本+期间费用+其他费用）/Q,其中,期间费用=管理费用+营业费用+财务费用。

供水公司的水价为Pm,自来水厂的水价为P,P0为受水区用户可承受水价。

假定以上参数变量满足关系：Pm ＞Cm,Pm + Cm ≤P ≤P0。

4）模型构建

该供应链上二者进行两阶段完全信息动态博弈。为计算简便,仅用Cm与Cr代替详细的成本要素,不考虑所得税,各自的利润函数以及供应链总利润函数分别为：

5）模型求解

①完全信息模式下双方非合作动态博弈分析

非合作动态博弈的第一阶段,供水公司花费单位成本Cm,以Pm的价格出售自来水,每单位水获得Pm - Cm 的利润；动态博弈的第二阶段,自来水厂根据供水公司的行动以及自身的配水成本Cr,确定销售价格P,每单位自来水获得P - Pm - Cr 的利润。双方之间属典型的Stackelberg 博弈关系。因此,可以根据逆向归纳法求解。

将式（4.5）代入式（4.2）,得到供水公司的利润函数：

将式（4.7）代入式（4.5）,得到自来水公司的最优水价为：

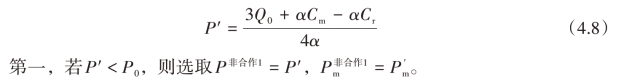
将式（4.8）代入式（4.1）,得到自来水的市场需求为：

将式（4.7）式（4.8）、式（4.9）分别代入式（4.2）、式（4.3）和式（4.4）,得到自来水厂和供水公司的利润以及非合作情形下的总利润分别为：

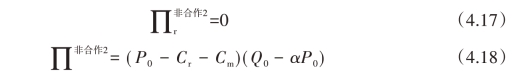
②完全信息模式下双方合作博弈分析

合作时,双方协议确定自来水的市价,以取得整体利润最大化,而后按照事先约定的利润分配方案进行利润分配,实现帕累托最优。

将式（4.19）代入式（4.1）得合作情形下的需求量为：

将式（4.20）代入式（4.2）,得到合作情形下供水公司的利润为：

将P合作1 = P″及式（4.20）代入式（4.4）,得到合作下整体的最优利润为：

第二,若P″≥P0,则选取P合作2 = P0。

合作情形下的需求量为：

将P合作2 = P0及式（4.23）代入式（4.4）,得到合作下整体的最优利润为：

③基于Shapely值法的双方合作博弈均衡解

供水公司和自来水厂因合作而成为一个收益共同体,但二者同时也在追求各自收益的最大化。本节采用Shapely值法对总利润进行分配。据前所述,Shapely值表达式为：

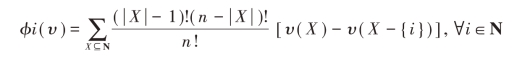
对于调水工程供应链而言,n = 2,供水公司的子集包括Xm ={供水公司},Xmr={供水公司,自来水公司},自来水厂子集包括Xr={自来水厂},Xmr={供水公司,自来水厂},|Xm|=1,|Xr|=1,|Xmr|=2,则供水公司和自来水厂可以分得的利润分配值分别为：

由式（4.21）和式（4.27）相等得供水公司的水价为：

所以这种情况下,合作并没有带来供应链整体利润的提高,所以二者没有动力选择合作。

6）供应链利益博弈均衡解

本节采用文献[149]对引洮调水工程水价体系研究中获得的农村生活用水、城镇生活用水和工业生产用水的数据作为实例进行算例分析。相关数据整理后见表4.20。

表4.20　各部类用水相关数据

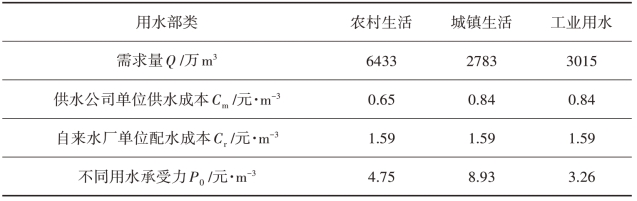
资料来源：需求量选取《引洮一期工程可行性报告》中2019年的需求量预测数据。其他数据取自骆进仁《供应链视角下多目标调水工程水价体系研究》,供水公司成本选取单位完全成本,自来水厂成本选取并入现有自来水厂模式下的单位成本,非合作下供水公司接受的水价选取文献中测算的引洮供水公司的水价。

①博弈均衡解

假设α = 500。将以上数据代入模型求解,计算结果见表4.21与表4.22。

表4.21　非合作博弈下供水公司以及自来水厂利润分配表

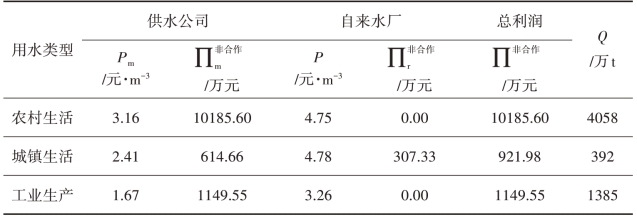
表4.22　合作博弈下供水公司以及自来水厂利润分配表

假设α = 1000,将以上数据代入模型求解,计算结果见表4.23与表4.24。

表4.23　非合作博弈下供水公司以及自来水厂利润分配表

表4.24　合作博弈下供水公司以及自来水厂利润分配表

基于上述计算结果,可以看出无论需求弹性是多少,合作有利的情况下均有,。基于Shapely 值分配模型的利润分配结果满足个体理性及整体理性,且达到了帕累托最优,即当供水公司和自来水厂组成一个联盟时,各自利润的分配达到了最优。

②修正的Shapely值法下的均衡解

由于传统的Shapley值法是按供应链成员对联盟的边际贡献大小来分配收益的,而将影响收益的其他因素,如风险因素、投资因素等,视为均等,但实际上很难达到那样的均等情况。按照一定的方法将不同影响因素加权因子合成到Shapely 值计算方法中,可以使得该法更合理、更科学。结合前人的研究,考虑投资因素以及风险因素对传统Shapley值法进行修正。(www.daowen.com)

假设有n个企业组成供应链联盟N={1,2,…,n},供应链总利润为υ(I),传统的Shapley 值法下企业i 的收益为φi(υ)。考虑风险因素以及投资额因素时,修正过程可以如下：首先,运用专家评分法得到n 个成员各自的风险因素向量,根据投资额大小计算出供应链的投资因素向量。然后,分别计算出风险因素以及投资因素的修正因子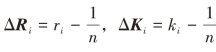。可知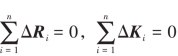。最后,可以采用专家评分法给出风险因子以及投资因子的权重向量f=（fR,fK）,fR +fK =1,于是可以得到企业i的综合修正因子ΔZi =fR×ΔRi +fK×ΔKi,企业i的修正收益为Δφi(υ)=υ(I)×ΔZi,最终得出企业i的修正后收益为φi(υ)′=φi(υ)+Δφi(υ)。

假定采用专家评分法给出风险因子及投资因子的权重向量为f =(0.4,0.6)。

假定采用专家评分法得到不同用水下供水公司和自来水厂的风险因素向量、风险因素的修正因子以及投资因素向量（供水公司和自来水厂的投资额采用单位用水成本投入来衡量）、投资因素的修正因子以及综合修正因子见表4.25、表4.26。修正后的利润分配情况见表4.27。

表4.25　风险因素以及投资因素修正因子表

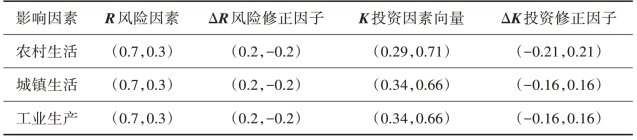
表4.26　供水公司和自来水厂综合修正因子表

表4.27　修正以后的利润表（万元）

对比修正前以及修正后的利润分配结果可以看出,修正Shapely值法下,合作时供水公司和自来水厂的利润额依旧均大于非合作下,所以模型依然是稳定的。修正后,供水公司的利润额有所降低而自来水厂的利润额有所增加,具体增减幅度因修正因子的大小而不同。说明修正可以促进二者利润分配上的公平。

（2）水资源供应链整体亏损下的博弈

1）问题描述

欠发达地区的承受力水价普遍偏低,特别是农业生产用水的承受力甚至不能弥补供水公司的运行成本。本书考虑政府补贴下的单个供水公司和单个自来水厂之间的博弈。对节点企业而言,所需投入的成本能否得到补偿决定了其是否愿意供水或者用水。用Cm及Cr分别表示供水公司和自来水厂的单位成本,用Q 表示市场需求,用P 表示自来水厂的水价,用πm 和πr 分别表示供水公司和自来水厂的收益,双方收益矩阵见表4.28。

表4.28　整体亏损下供水公司和自来水厂收益矩阵

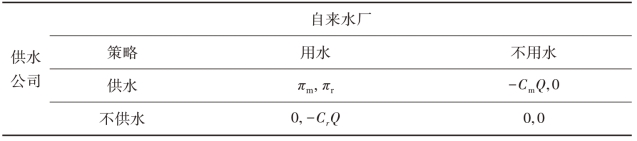
P ＜Cm + Cr 时,πm + πr = PQ -(Cm + Cr)Q ＜0,也就是说,如果自来水厂的水价低于供应链的单位成本之和,那么无论双方按照何种规则分配利润,结果必定至少有一方的收益为负,而收益为负的一方必然不愿供水或者用水,另一方最好也选择不用水或者不供水,于是双方的均衡收益为（0,0）,这是一个典型的纳什均衡。

引入政府补贴因素后,如果补贴金额及补贴权重的选取能使收益转变为πm ≥0,且πr ≥0 时,考虑到政府作用以及企业社会责任等因素,双方就会有意愿选择（供水,用水）策略组合。已有的研究也说明,政府补贴并不是越多越好,过多的补贴一方面会加重政府的负担,也可能导致企业的“寻补贴”行为,所以政府希望以最小的补贴金额达到促使供水公司和自来水厂选择（供水,用水）策略组合的目的。

2）模型假设

第一,博弈参与人包括政府、供水公司以及自来水厂（含农民用水者协会）,三者都是理性经济人。由于政府只起调节的作用,因此具体的博弈在供水公司和自来水厂之间进行。

第二,政府的策略集为{均补贴,仅补贴供水公司,仅补贴自来水厂,均不补贴},供水公司的策略集为｛供水,不供水｝,自来水厂的策略集为｛用水,不用水｝。决策顺序为：政府→供水公司→自来水厂。

第三,除了供水公司以外,自来水厂没有别的水源可用。

第四,自来水的需求函数为：

Q0表示最大需求量,Q0 ＞0,α为需求量对水价的敏感系数,α ＞0。Q 等于供水公司的供水量或自来水厂的用水量,Q ＞0。双方的供水量等于制水量。

3）变量说明

依照财务会计核算方法核算供水公司以及自来水厂的总成本,并分摊为单位成本。

供水公司的单位成本Cm=（基本折旧费+运行费用+流动资金利息）/Q,其中,运行费用=工程维修费+工资福利费+工程管理费+动力费+其他费用。

自来水厂的单位成本Cr=（主营成本+期间费用+其他费用）/Q,其中,期间费用C r1=管理费用+营业费用+财务费用。

［农民用水者协会单位配水成本Cr=（管理人员工资+管理费用+维修养护费）/Q。］

Pm和P分别表示供水公司和自来水厂的水价,P0表示承受力水价。

政府补贴总额为S = Sm + Sr,供水公司的补贴额为Sm= bS,自来水厂的补贴额为Sr=(1 - b)S,0 ≤b ≤1。

假定上述参数变量满足Pm ≤P ≤P0,P - Cm - Cr ＜0。

4）模型构建

为计算简便,仅用Cm 与Cr 代替详细的成本要素,不考虑所得税,供水公司、自来水厂（含农民用水者协会）以及供应链总体的利润函数分别为：

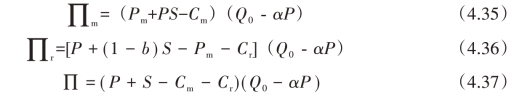
5）模型求解

①完全信息模式下双方非合作动态博弈

博弈开始,首先由供水公司确定水价Pm,自来水厂再视情况确定市价P,双方形成了典型的Stackelberg博弈关系,可以根据逆向归纳法求解。

将式（4.38）代入式（4.35）,得到供水公司的利润函数：

将式（4.40）代入式（4.38）,得到自来水公司的最优水价为：

将式（4.41）代入式（4.34）,得到自来水的市场需求为：

将式（4.40）、式（4.41）、式（4.42）分别代入式（4.35）、式（4.36）和式（4.37）,得到供水公司、自来水厂以及供应链总利润分别为：

②完全信息模式下双方合作博弈分析

将式（4.51）代入式（4.34）,得到合作下自来水的需求量为：

将式（4.51）、式（4.52）代入式（4.35）、式（4.37）,分别得到合作下供水公司以及供应链整体的利润为：

此时需求量为：

③基于Shapley值法的合作博弈均衡解

合作时,双方追求总利润最大的同时,也在追求利润分配上的帕累托最优。采用Shapely 值法对供应链的总利润进行分配。据前所述,Shapely 值法表达式为：对模型而言,n = 2,供水公司的子集包括Xm={供水公司},自来水厂子集包括Xr={自来水厂},Xmr={供水公司,自来水厂},|Xm|=1,|Xr|=1,|Xmr|=2,供水公司和自来水厂的利润分配值分别为：

供水公司的水价为：

供水公司的水价为：

6）供应链整体亏损下利益博弈均衡解

本节采用文献[149]对引洮工程水价体系研究中获得的农业用水的相关数据作为实例进行算例分析。相关数据见表4.29。

表4.29　引洮工程成本及需求数据表

资料来源：成本取骆进仁《供应链视角下多目标调水工程水价体系研究》中的数据,最大需求量取《引洮一期工程可行性报告》中2019年的需求量预测数据。

假定α = 1000,S 分别取0、0.2、0.24 以及0.25,将以上数据代入模型求解,计算结果见表4.30、表4.31、表4.32及表4.43。

表4.30　无补贴时调水工程利润计算表

当S = 0 时,非合作下,供水公司会凭借主导地位率先选择P0 作为最优水价,而农民用水者协会也只有选择P0时才能避免更大的亏损。合作时,双方只有协议把市价定为P0 时,才能使∏最大,也就是总亏损额最低。但是由于∏非合作= ∏合作,合作并不能带来利润分配上的帕累托最优,所以二者没有合作的动力。非合作时,由于P0 的约束以及S = 0 的影响,∏m＜0 且∏r＜0,所以二者会选择（不供水,不用水）策略组合。

表4.31　补贴金额为0.2元/m3时引洮工程利润计算表

当0 ＜S ＜Cm - P时,非合作下供水公司和农民用水者协会仍会把P0作为自己的最优价格,合作下二者最好把市价仍定为P0。此时∏非合作= ∏合作,所以双方依旧没有合作的动力。当0 ＜S ＜Cm - P 时,非合作下,无论b 取多少,均有∏m ＜0,而b 取值较小时,可能存在∏r ＞0,这种情况下二者的最优策略组合仍然是（不供水,不用水）。

表4.32　补贴金额为0.24元/m3时调水工程利润计算表

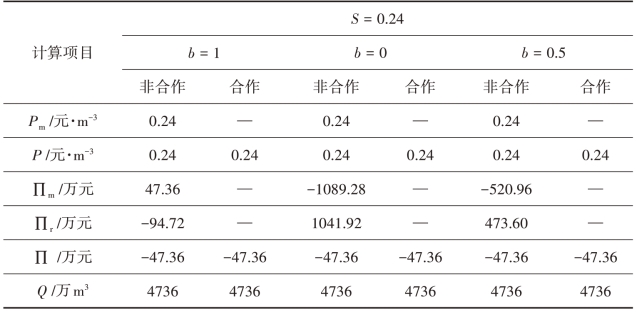
当Cm - P ≤S ＜Cm + Cr - P 时,无论b 等于多少,总有∏非合作= ∏合作,所以双方仍选择不合作。非合作下,二者的最优定价均为P0,b 的取值越大,∏m越大,∏r越小,但是二者总是一正一负,所以供水公司和农民用水者协会的最优策略组合仍然是（不供水,不用水）。

表4.33　补贴金额为0.25元/m3时引洮工程利润计算表

当S = Cm + Cr - P 时,仅当取b = 0.92 时,∏m=0,∏r=0,此时相比（不供水,不用水）策略组合,考虑企业社会责任以及其他因素的作用,二者最好选择（供水,用水）策略组合。政府以最小的补贴金额,促使引洮工程发挥应有的作用,这对三者均有利。