现在来看把d、q轴放在任意位置或以任意角速度旋转时得到的电机模型是怎样的。设d、q处于图A-4所示的位置，并以任意角速度ω_k旋转，它相对于定子a相绕

组转过的角度用γ来表示，。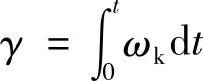

图A-4 任意坐标系d、q轴绕组

如前所述，α、β轴上有等效两相电机的绕组。这样考虑不失一般性，因为总是可以用坐标变换把任意相电机等效为两相电机。α、β轴上的变量等效到d、q轴上的坐标变换分别为

定子：

转子：

所以

同理可得

可见此时的磁链表达式和式（A-11）完全相同。

现在再来看一下在上述坐标变换下的电压和转矩表达式。

（1）电压表达式

对于转子电压方程来讲，除角度变为γ-θ外，其他各项均类似于定子电压式，即把下标s换为r即可。又因

因此得电压表达式

（2）转矩表达式

方程式（A-16）、式（A-17）即为坐标轴d-q放在任意位置或以任意角速度旋转时的派克方程，也称为广义派克方程。此时，考虑了零轴分量后从三相电压到d-q轴的电压变换矩阵为B_s^-1C^-1，即派克变换：

这里得到的变换矩阵的系数是规格化（即单位化）的结果，此矩阵求逆非常方便，只要把原矩阵转置即可，在分析计算时，避免了从实际值到标幺值的折算。下面来看一下广义派克方程的复变形式。(www.daowen.com)

首先把广义派克方程的电压表达式写成矩阵形式，并以电流为状态变量，即

上述矩阵包含的四个子矩阵都具有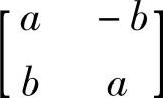的形式，不难求出此矩阵的特征值为一对共轭复数：λ=a±jb。

求出相应的特征矢量，即得使其对角化的变换矩阵

根据能量守恒定律，可求出系数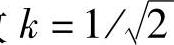，且S₂的逆矩阵为其共轭转置矩阵。这样就得到了复变量和d-q轴变量之间的变换矩阵，考虑到零轴分量后变为

式中

此即Ku变换（Ku即顾毓琇）。

当d、q轴放在定子、转子或旋转磁场上时，就分别给出著名的1-2-0变换（Fortescue），F-B-0变换（即前进—后退变换），F_c-B_c-0变换。例如d、q轴放在定子上时：B_s^-1=I，所以

由于u_s+和u_s-的表达式完全共轭，因此仅列出电压表达式的正序分量，得

把上述方程中的电流变量换为磁链的话，可得如下表达式：

也即（见图A-6）：

图A-5 三相及两相等效电机

现在对已知的所有电机模型坐标变换做一总结。设三相电机和两相等效电机的绕组如图A-5所示，d、q轴的位置为任意，各变换关系见表A-1。

不同坐标系下的电机模型应用于电机过渡过程的分析所得的结论已为大家熟悉^[1、2]，不过当它应用于交流电机尤其是异步电机的控制时，同样导致了重要的结果，如矢量控制技术的问世就标志着交流电机控制领域的一场革命。德国工程师Blascheke提出的转子磁场定向矢量控制技术目前得到了最广泛的应用。这种方法把d、q轴放在旋转磁场上，并使d轴方向和转子磁通矢量重合，就导致转子方程和转矩方程的简化，使得过去颇为头疼的异步电机控制问题变得和直流电机一样可行了。不过，在转子磁场定向矢量控制中，需检测转子磁场的位置和大小，由于转子参数受温度化影响很大（可达50%），所以为解决这个问题，系统变得越来越复杂。为此，我们提出了定子电压定向矢量控制的方法，较好地解决了系统复杂性与转矩和磁通的解耦控制问题^[4]。

图A-6 异步电机复变量模型