由方程式（A-1）～式（A-3）可知，即使在简化的情况下，这些关系也是很复杂的，由于电感系数是随时间变化的，因此利用这些方程来研究电机的运行相当困难。

首先让我们纯粹地从数学意义上来看如何化简方程式（A-1）中的系数矩阵，例如L_s，此矩阵为对称矩阵，我们目的是通过适当的坐标变换矩阵C使其化简，具体讲即对角化。为使矩阵对角化，首先须求出矩阵的特征值，令

det（L_s-λI）=0即

展开得

解得重根为

L_s=L_ss-M_s （L_s为等效两相定子自感）单根为

L_s0=L_ss+2M_s （L_s0为等效零轴电感）变换后的电感矩阵为

将特征值L_s、L_s0代入矩阵L_s所表示的方程式组中，可解得对应的特征矢量应满足的关系式：

对应于重根λ=L_ss-M_s，有

X₁+X₂+X₃=0 （A-4）

对应于单根λ=L_ss+2M_s，有

X₁=X₂=X₃ （A-5）

因为任何性线变换均不改变系统的物理本质，根据能量守恒定律，变换前后的能量表达式应该是相等的，即

u^T_s is=u^T_sNC^TCi_sN由此得出

C^TC=I即

C^-1=C^T可见C必为正交矩阵。我们又知道，两相电机和三相电机一样，也同样可以产生旋转磁场，这也为变换后的电感系数矩阵所证明，它包含一个零轴等效电感的和一个两相等效电感。现在我们就和用三相电机和两相电机之间的关系来确定变换矩阵C的值。

图A-2 等效两相电机模型

设有图A-2所示的两个电机（一个为三相电机，另一个为等效两相电机），等效两相电机的定子绕组为S_α、S_β。注意：这里我们借用了大家所熟悉的α-β-0坐标系的符号，但意义是不同的。

设N₂、N₃分别为两相和三相电机绕组的有效匝数，等效的条件是气隙中产生的磁通相等，即B_3m=B_2m。而

欲使两式相等，则有

将上式写成矩阵形式并考虑零轴分量后得变换矩阵C-1

此矩阵的各矢量满足前述特征矢量的条件式（A-4）、式（A-5），即为所求的变换矩阵（即Clark变换矩阵）。现在将此矩阵规格（单位）化，以求得系数N₃/N₂和x。由(www.daowen.com)

得

由

得

最后得Concordia变换矩阵

对L_r、L_sr（θ）=L_rs（θ）T和电压、电流做同样的变换，由L_N=C^-1LC得

式中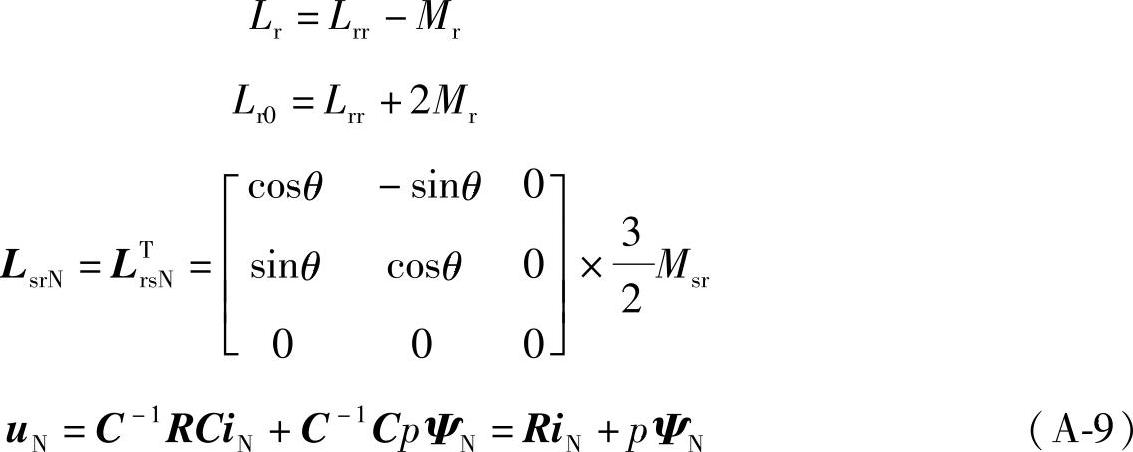

此变换相当于在定子和转子上分别用两相绕组代替三相绕组，因此在L_srN=L^T_rsN中还存在cosθ、sinθ项，使得电压和转矩表达式的系数中始终存在着时变量，计算起来还是很不方便。现在我们就用新的变换来导出参数坐标轴放在定子上的电机动态方程。

因为在中点不接地的电机中，零轴分量不产生跨过气隙的基波磁通，也就不出现在转矩表达式中，因此在以下的分析中可将它略去不计。现在只考虑等效两相电机的磁通表达式

将定子磁通表达式展开得

设：

则得到一个新的变换矩阵

使得

注意到B为单位正交矩阵，即B^-1=B^T。它的物理意义可通过图A-3来解释，相当于用s_α、s_β轴上的变量i_rd、i_rq来代替i_rα、i_rβ，条件是在气隙中产生相同的磁动势。通俗地讲，就是把转子上的变量通过旋转变换移到定子上来分析。

图A-3 旋转变换关系

对转子磁通做同样的变换后可得新的坐标系中的磁通表达式

在以上的分析中，借用了众所周知的d-q-0坐标系的符号，但要注意到它们实际的区别。现在来看在新的坐标系下电压和转矩的表达式。由方程式（A-1）得定子电压表达式

即

转子电压表达式

即

电磁转矩表达式

式（A-12）～式（A-14）实际上就是把坐标轴放在定子上的派克方程，也就是众所周知的α-β-0坐标系下的电机模型。但如果仅仅到此为止，那么除做了α-β-0变换的数学证明之外没有什么意义。下面将要做的是把B变换推广到任意坐标轴上，以得出广义派克方程。