用模型参考自适应法（Model Reference Adaptive System——MRAS）辨识参数的主要思想是将不含未知参数的方程作为参考模型，而将含有待估计参数的方程作为可调模型，两个模型具有相同物理意义的输出量，利用两个模型输出量的误差构成合适的自适应律来实时调节可调模型的参数，以达到控制对象的输出跟踪参考模型的目的。

C.Schauder首次将模型参考自适应法引入导步电机转速辨识中，这也是首次基于稳定性理论设计异步电机转速的辨识方法，其推导如下。

静止参考坐标系下的转子磁链方程为

据此构造参数可调的转子磁链估计模型为

认为估计模型中ω是需要辨识的量，而认为其他参数不变化。式（5-60）和式（5-59）可简写为

式中

定义状态误差为

则式（5-62）减式（5-61）可得

根据Popov超稳定性理论，取比例积分自适应律K_p+K_i/s，可以推得角速度辨识公式为

式中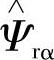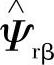，、由转子磁链的电流模型即由式（5-59）获得，而Ψ_rα、Ψ_rβ由转子磁链的电压模型即由式（5-65）和式（5-66）获得。

辨识算法框图如图5-30所示。正如在介绍磁链观测方法时所提到的，这种方法在辨识角速度的同时，也可以提供转子磁链的信息。

图5-30 模型参考自适应角速度辨识算法框图

由于C.Schauder仍然采用电压模型法转子磁链观测器来作为参考模型，电压模型的一些固有缺点在这一辨识算法中依然存在。为了削弱电压模型中纯积分的影响，Y.Hori引入了输出滤波环节，改善估计性能，但同时带来了磁链估计的相移偏差，为了平衡这一偏差，同样在可调模型中引入相同的滤波环节，算法如图5-31所示。

图5-31 带滤波环节的MRAS角速度辨识算法

经过改进后的算法，在一定程度上改善了纯积分环节带来的影响，但仍没能很好地解决电压模型中另一个问题——定子电阻的影响。低速的辨识精度仍不理想，这也就限制了控制系统调速范围的进一步扩大。

前两种方法是用角速度的估算值重构转子磁链作为模型输出的比较量，也可以采用别的量，如反电动势。由于转速的变化在一个采样周期内可以忽略不计，即认为角速度不变，对式（5-59）两边微分，可得反电动势的近似模型为

经与磁链模型类似的推导，可得角速度辨识公式为(www.daowen.com)

式中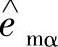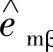，、β^由式（5-67）估计获得，而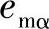、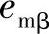由参考模型式（5-69）和式（5-70）求得。

用反电动势信号取代磁链信号的方法，去掉了参考模型中的纯积分环节，改善了估计性能，但式（5-67）的获得是以角速度恒定为前提的，这在动态过程中会产生一定的误差，而且参考模型中定子电阻的影响依然存在。

由于定子电阻的存在，使辨识性能在低速下没有得到较大的改进。解决的办法：一是实时辨识定子电阻，但无疑会增加系统的复杂性；二是可以从参考模型中去掉定子电阻，采用无功功率模型，正是基于这一考虑，令

无功功率可表示为

式中，⊗表示叉积。

将式（5-69）和式（5-70）写成复数分量形式为

由于i_s⊗i_s=0，将式（5-72）代入式（5-71）得

以式（5-73）作为参考模型，以式（5-67）求得的与i_s叉积的结果式（5-74）作为可调模型的输出，同样可以推得角速度表达式为式（5-75）。

显然，这种方法的最大优点是消除了定子电阻的影响，为拓宽调速范围提供了新途径。另外一种以无功形式表示的参考模型为

该式可直接根据实测电压、电流计算得出，与任何电机参数都无关。当假设转子磁链变化十分缓慢，可以忽略不计而认为磁链幅值为恒定时，可以近似得到反电动势表达式为

进而得到定子电压方程式为

可调模型可表示为

由Popov超稳定性理论，可推出定子角速度表达式为

将其减去转差角速度ω_sl，得角速度推算表达式为

这种方法也同样消去了定子电阻的影响，有较好的低速性能和较宽的调速范围，然而这种方法基于转子磁链幅值恒定的假设，因而辨识性能受磁链控制好坏的影响。

总的来说，MRAS是基于稳定性设计的参数辨识方法，它保证了参数估计的渐进收敛性。但是由于MRAS的速度观测是以参考模型准确为基础的，参考模型本身的参数准确程度就直接影响到速度辨识和控制系统工作的成效，解决的方法应着眼于：①选取合理的参考模型和可调模型，力求减少变化参数的个数；②解决多参数辨识问题，同时辨识转速和电机参数；③选择更合理有效的自适应律，替代目前广泛使用的PI自适应律，努力的主要目标仍是在提高收敛速度的同时，保证系统的稳定性和对参数的鲁棒性。