在直接转矩控制系统中，转矩控制是最重要的，下面对其性能进行分析。

对式（5-5）T_em=p_n（Ψ_s⊗i_s）两边取微分，再同乘以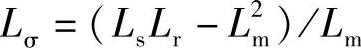，得

由式（5-3）推导出

式中，τ_r为转子时间常数，τ_r=L_r/R_r。

对式（5-20）两边微分，再代入式（5-21）可得

将式（5-2）、式（5-3）和式（5-22）代入式（5-19），整理可得

因为

所以

式中

式（5-24）中，T_em、Ψ_s、Ψ_r及ω在一个采样周期内的变化相对于外加激励电压u_s的变化可忽略不计，即认为基本恒定不变，也就是说影响瞬间转矩变化的主要因素是u_s。在直接转矩控制中，只需在一拍内实现u_s有明确的突变，就可使转矩迅速变化，这一点是传统矢量控制无法做到的。因而，在电机、逆变器允许的条件下，尽可能地提高直流母线电压U_d和缩短采样控制周期，就可以获得高动态的转矩响应。

由（5-24）式不难看出，当Ψ_r和u_s垂直时，转矩响应是最快的。但由于Ψ_r和u_s之间的关系比较复杂，而定子磁链Ψ_s和u_s的关系比较简单，在直接转矩控制系统中，是对Ψ_s进行直接控制的。这就要求Ψ_s和Ψ_r的相角和幅值都不能相差过大，否则就会造成控制失败，其关键就在于定子电流的控制。

对式（5-20）（L_r/L_m）Ψ_s=Ψ_r+Lσi_s进行分析，由于

在Lσ通常很小的情况下，当限制i_s≤1.5I_N时，由于漏磁通降落很少，所以此时定子磁链和转子磁链无论在相位还是幅值上均很接近，即Ψ_r≈Ψ_s。图5-5的仿真结果也很好地证明了这一点。(www.daowen.com)

在直接转矩控制系统中，无论是基于逆变器的安全使用还是控制策略的要求，限流措施都是必需的。通常可以将电机定子绕组三相短路，即逆变器输出零矢量，来达到限流的目的。

图5-5 定转子磁链幅值相位比较

将Ψ_r≈Ψ_s代入式（5-24）得

从这个动态转矩公式可以知道，施加的电压矢量与当前定子磁链相垂直时，能够得到最大的转矩变化量。但对于电压型逆变器来说，在直接转矩控制系统中，可供选择的矢量只有8个，每一时刻都按垂直磁链方向90°施加电压矢量是不可能的，但可以选择包含这个90°方向矢量的两个非零矢量之一，从综合的效果来看，是没有区别的。

单纯从数学式（5-25）上来看，不难得到以下结论：

●当施加超前于定子磁链的电压矢量，使dT_em/dt＞0时，转矩将会增加。

●当施加落后于定子磁链的电压矢量或零矢量，使dT_em/dt＜0时，转矩将会减小。

从物理概念上也很容易解释。

由式（5-26）可知，电磁转矩的大小是由转子磁链和定子磁链之间的叉积来决定的。在实际系统运行中，控制定转子磁链的幅值基本不变，要改变电磁转矩的大小，可以通过改变定转子磁链间的夹角来实现。而转子磁链的旋转速度不会突变，因而，这又主要是通过改变定子磁链的旋转速度来达到改变转矩这一目的的。

当施加超前定子磁链90°的电压矢量时，定子磁链的旋转速度最大，因而前进的角度也最大，相应获得的转矩变化量也最大，这与前面的数学分析是一致的。一般地，当施加超前矢量使定子磁链的旋转速度大于转子磁链的旋转速度时，磁链夹角加大，相应地转矩增加。同样，如果施加零矢量或滞后矢量，相当于定子磁链矢量停滞不前或反转，而转子磁链矢量继续旋转，磁链夹角减小，相应地转矩减小。

可以看出，数学和物理上的解释是一致的。事实上，直接转矩控制技术中，其基本的控制方法就是通过电压空间矢量来控制定子磁链的旋转速度，控制定子磁链走走停停，以改变定子磁链的平均旋转速度，从而改变定转子磁链的夹角，以达到控制电磁转矩的目的。