上述转子齿谐波法中，所检测的谐波是在基波激励下形成的，由于在低速下信号强度弱、易受噪声干扰、不易进行谱分析等原因，造成了以上提到的一些问题，如何进行改进呢？

Lorenz等学者另辟蹊径，不使用基波激励产生的谐波，而是通过在电机接线端上注入一个三相平衡的高频电压信号，利用人为造成的（如对电机进行改造）或内部寄生的不对称性，使电机产生一个可检测的磁凸极，通过对该磁凸极位置的检测来获取转速信息，这里称为凸极跟踪法，下面简单介绍其原理。

假设注入的高频电压信号角速度为ω_i，ω_i>>ω_s，幅值为u_si，则

高频信号注入下的异步电机等效电路可简化为图4-35所示。令

Z_s≈jω_iL_sα （4^-143）同时

对一个定子或转子存在不对称性的异步电机来说，在同步旋转坐标系下，d、q轴所对应的L_sσ不相等，分别记为L_sσd和L_sσq，且L_sσd≠L_sσq，表示成矩阵形式为

在静止坐标系内，可表示为

式中，∑L_sσ=（L_sσd+L_sσq）/2；ΔL_sσ=（L_sσq-L_sσd）/2；θ_r为转子位置。

图4-35 高频信号注入下的异步电机简化等效电路

把式（4-146）和式（4-142）代入式（4-144）并整理得

式中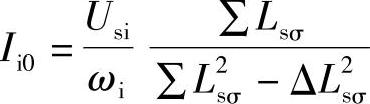

不难看出，高频激励产生的高频电流信号中，包括I_i0的一项与转子位置无关，而包含I_i1的一项与转子位置有关，所以应设法去掉I_i0的干扰而只留下I_i1，这可以通过以下几步做到。首先令(www.daowen.com)

式中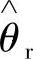，为转子位置的估计值。再将式（4-147）代入式（4-148）可得

然后，用低通滤波器滤去式（4-149）中右端第一项，得

由式（4-150）可知，通过调节ε_f使之趋于零，即可得到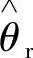趋于θ_r，也就是转子位置的估计值收敛于真实值，当取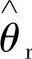的微分时，就能获得转子角速度

图4-36给出了这种方法的算法框图。

图4-36 凸极跟踪法算法框图

图4-37表明了如何获取图4-36中所需的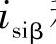和。

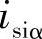图4-37 高频信号注入下的凸极跟踪法

图4-37中，下标f表示基波，下标i表示高频信号。

由以上分析不难看出，这种凸极跟踪的方法不取决于任何电机参数和运行工况，因而可能工作在极低速甚至零速运行状态，并且系统的计算工作量并不大，可以说是目前无速度传感器控制中较理想的方法。

此外，还有J.Jiang和J.Holtz的漏感脉动检测法、S.K.Sul的dq阻抗差异定向法、Blaschke的饱和凸极检测法等，这几种基于电机非理想特性的无速度传感器方案为实现无速度传感器控制在极低速下的应用提供了新的思路。