矢量控制技术得以有效实现的基础在于异步电机磁链信息的准确获取。为了进行磁场定向和磁场反馈控制，需要知道磁链的大小和位置。在任意速度旋转坐标系下，定、转子及气隙磁链的方程式为

定子磁链：

转子磁链：

气隙磁链：

式（4-66）中的第一个式子乘以L_r减去式（4-67）中的第一式与L_m的乘积，再经整理得

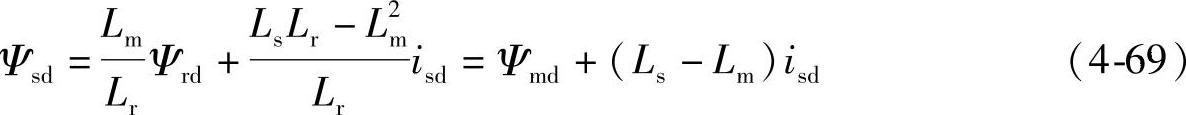
同理可得

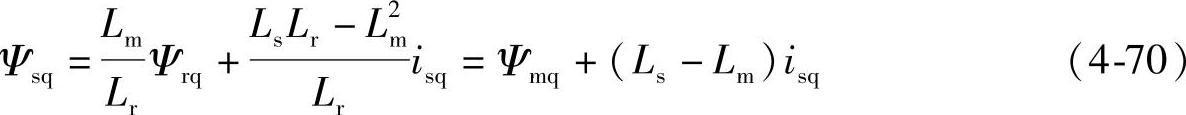
由式（4-66）～式（4-70）不难看出：①磁链表达式与转速无关；②定子、转子、气隙磁链三者只要知道其一，另外两个就可推得。因而，在矢量控制中，无论是采用α-β坐标系还是d-q坐标系，表达式形式是一致的，而且观测出三个磁链中的任何一个都可得到另外两个值。为叙述简便计，本书以转子磁链的状态估计为例介绍异步电机的磁链观测模型。读者在应用过程中，可根据所采用的定向系统，选择所需要的相应磁链信息，并可将下面给出的转子磁链模型代入式（4-69）、式（4-70）求解，以获得该磁链。

转子磁链信息的获得，最初采用的直接检测气隙磁链的方法：一种是在电机槽内埋设探测线圈；另一种是利用贴在定子内表面的霍尔片或其他磁敏元件。利用被测量的气隙磁链，由式（4-69）、式（4-70）得

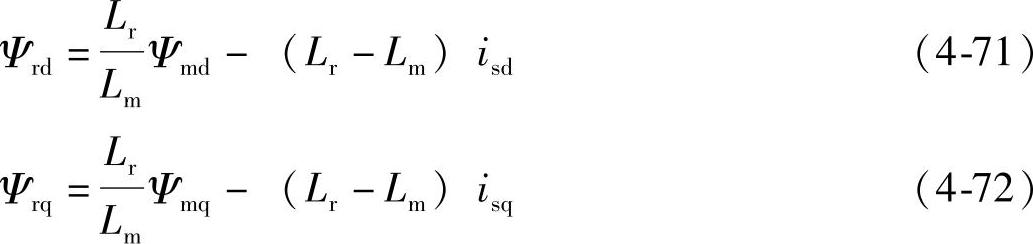
这就是转子磁链观测最直接的方法，而且具有显著的优点，只需要两个电机参数：一个是与温度和磁通大小无关的常值——转子漏电感L_r-L_m（闭槽转子除外），另一个是稍微受电机主磁路饱和程度影响的L_r/L_m。从理论上说，这种方法应该比较准确，但实际上，埋设线圈和敷设霍尔元件都会遇到不少工艺和技术问题，而且在一定程度上破坏了电机的机械鲁棒性。同时由于齿槽的影响，检测信号中脉动分量较大，转速越低时越严重。另一类特殊的问题将会在闭合转子槽电机（笼型异步电机的典型结构之一）中出现，这是由于此时转子漏电感强烈地取决于转子电流，尤其是当转子电流比较小时，如果不采取适当措施，磁链检测误差会相当大。因此，现在实用的系统中，多采用间接观测的方法，即利用容易检测的电压、电流或转速，借助异步电机数学模型，计算转子磁链的幅值和相位。

利用能够实测的物理量的不同组合，可以获得多种转子磁链观测模型，但总的来说，可以分成两类：开环观测模型和闭环观测模型。

1.开环观测模型

这种方法是直接从异步电机数学模型推导出转子磁链的方程式，并将该方程式视为转子磁链的状态观测器。

（1）电压模型法（根据定子电流和定子电压的检测值估算Ψ_r） 在α-β坐标系下，由定子电压方程和磁链方程易推导出

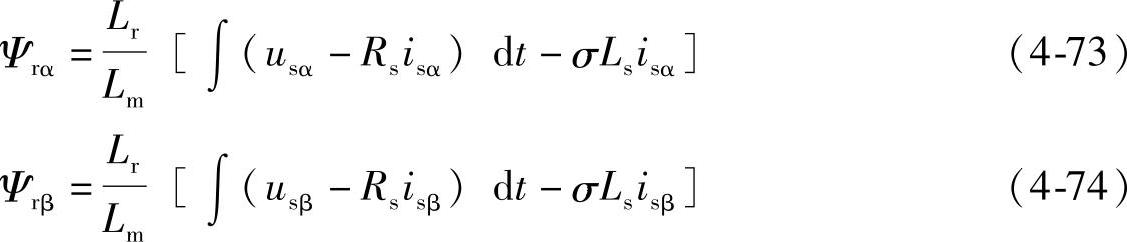
图4-20给出了其运算框图。

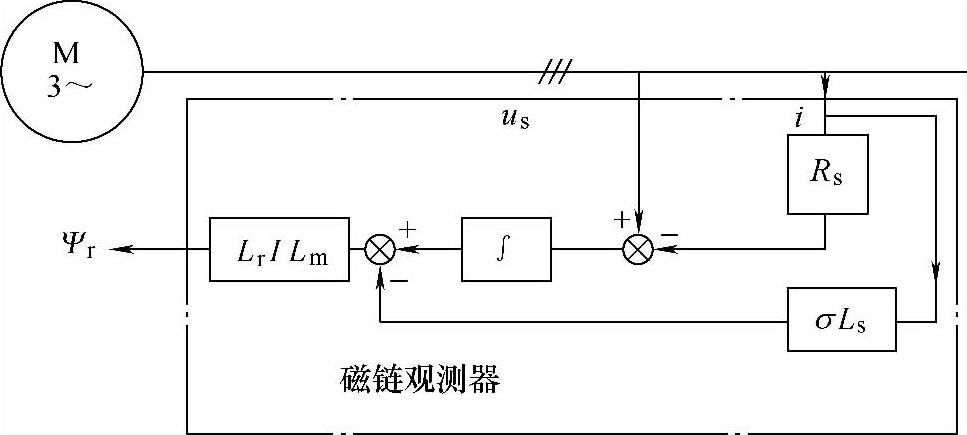
图4-20 电压模型法转子磁链观测器

电压模型法转子磁链观测器实质上是一纯积分器，其优点是：①算法简单；②算法中不含转子电阻，因此受电机参数变化影响小；③不需转速信息，这对于无速度传感器系统颇具吸引力。它的缺点是：①低速时，随着定子电阻压降作用明显，测量误差淹没了反电动势，使得观测精度较低；②纯积分环节的误差积累和漂移问题严重，可能导致系统失稳。这些局限性决定了这个方案在低速下不能使用，但是在中高速的合理范围内，它依然是可行的，而且也确实被应用于许多场合中。

（2）电流模型法（根据定子电流和转速检测值估算Ψ_r） 同样可在α-β坐标系下推得

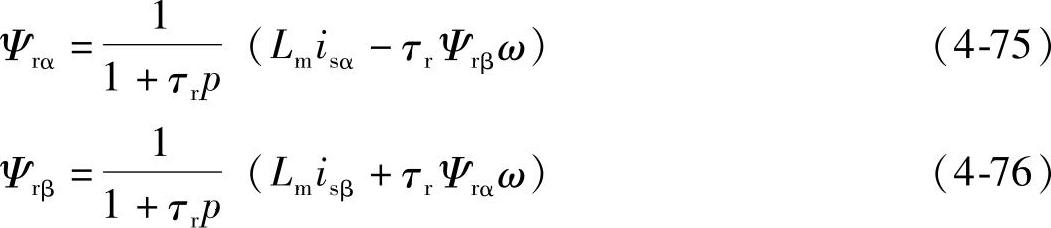
图4-21即是其运算框图。

可以看出，与电压模型法不同之处在于，电流模型法使用了角速度ω作为其输入信息。另外，它还涉及到时变特性显著的参数，即转子时间常数τ_r。当电机的运行温度发生变化或磁路出现饱和时，τ_r变动范围较大，常需进行实时辨识才能保证磁链观测精度。但由于电流模型法不涉及纯积分项，其观测值是渐近收敛的，这是它的一大优点，同时低速的观测性能强于电压模型法，但高速时不如电压模型法。

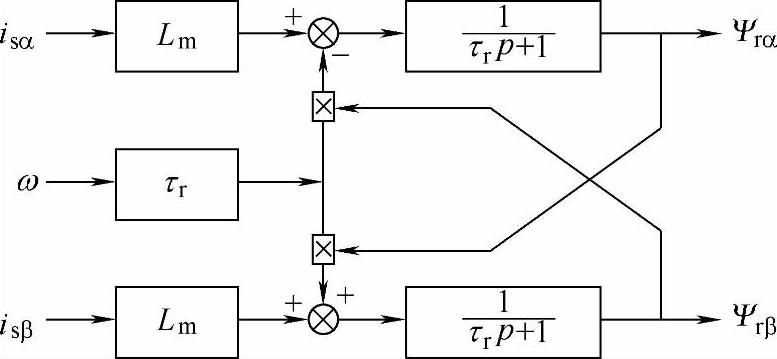
图4-21 电流模型法转子磁链观测器

（3）组合模型法（电压、电流模型相结合的方法） 从数学本质上看，磁链观测的电压和电流模型描述的是同一个物理对象，不同模型的使用之所以造成不同计算精度，其主要原因是由于参数和检测精度的影响，并非物理过程的变化。因此，考虑到电压模型和电流模型的各自特点，将两者结合起来使用，即在高速时让电压模型起作用，通过低通滤波器将电流模型的观测值滤掉；在低速时，让电流模型起作用，通过高通滤波器将电压模型观测值滤掉。为了实现两个模型的平滑过渡，可令它们的转折频率相等，即

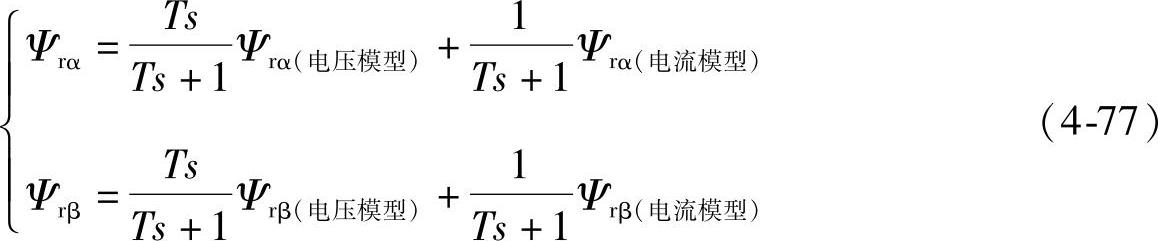
这种过渡用数字方式实现起来是很方便的，结果也是令人较为满意的。

（4）改进电压模型法 电压模型法不需要转子回路信息，其设计是基于定子回路动态方程完成的，这是它的一个显著优点，但同时也存在如前所述的一些缺点。为了保持电压模型法转子磁链观测器的优点，并克服其存在的缺陷，这里介绍一种改进的电压模型法，其原理如图4-22所示。

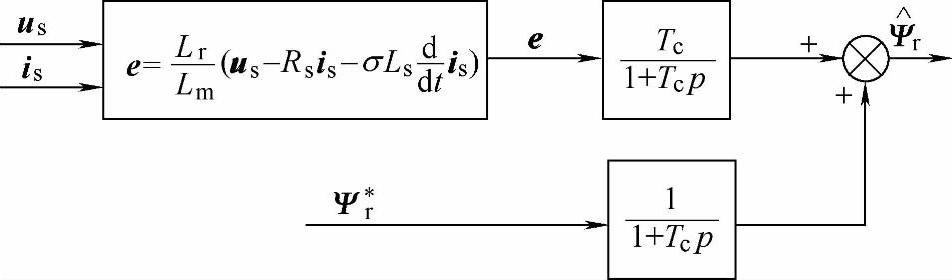
图4-22 改进电压模型法转子磁链观测器

从图4-22可以看出，这种转子磁链观测器取消了普通电压模型法关于反电动势e的纯积分环节，而代之以一阶惯性滤波环节，惯性环节产生的状态估计相位滞后由参考转子磁链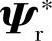的滤波信号来补偿，转子磁链状态估计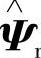的动态方程如下：

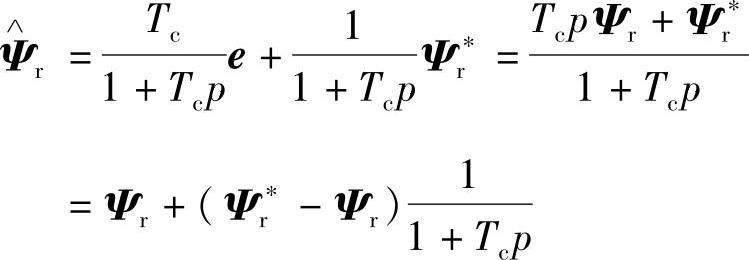
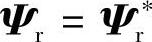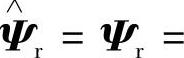
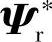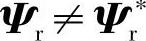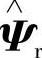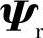在理想情况下，假设励磁的初始值，则误差为零，恒有。在一般情况下，初始值，将引起Ψ_r的动态收敛过程，其收敛特性取决于滤波环节的时间常数T_c，但这并不影响对的绝对收敛性。而且定子电阻R_s的变化引起的估计偏差可以通过选择合适的惯性环节时间常数T_c来加以削弱，例如可取T_c=τ_r，定转子漏感参数的变化在高速时会对状态估计产生重要影响。

（5）旋转坐标系下转子磁链观看模型 前几种方法均为α-β静止坐标系下的观测模型，在磁场定向控制中，有时会用到旋转坐标系下的转子磁链观测模型。转子磁场定向控制中，电机磁链观测模型可写成

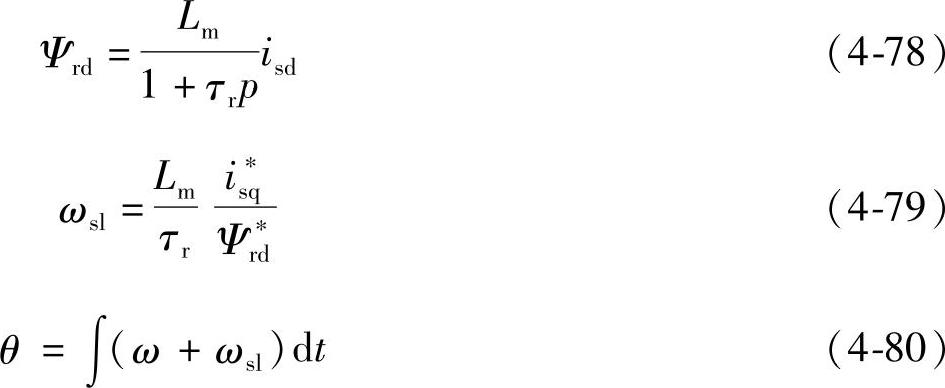
当给定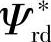、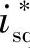q^时，由式（4-78）和式（4-80）就可定出转子磁链的幅值和角度，其运算框图如图4-23所示。

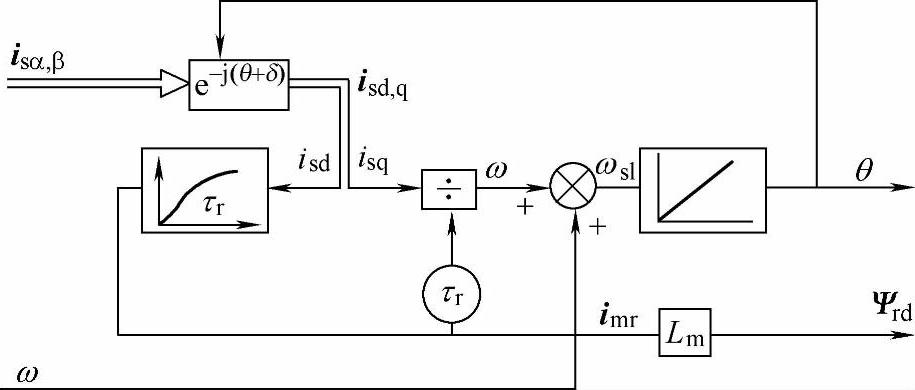
图4-23 旋转坐标系下转子磁链观测

2.闭环观测器

（1）基于误差反馈的转子磁链观测器 上述采用的开环估计法具有结构简单、实现方便等优点，但其精度受参数变化和外来干扰的影响较大，鲁棒性较差。究其原因在于，模型中缺少对各种干扰的抑制，尤其是电压模型法中表现更为明显。我们知道，在控制系统中抑制干扰最有效、最简单的方法是引入各种反馈措施，这在状态观测器的设计中表现为状态误差反馈环节的引入，它可以有效地改善状态观测器的稳定性，并提高状态估计精度。为此，将首先讨论基于误差反馈的转子磁链观测器的设计。该原理的构成框图如图4-24所示。从图中不难看出，这种转子磁链观测器实质上由两部分组成：①开环观测模型，一般为电压模型或电流模型；②误差反馈环节，异步电机的可测量定子电压u_s、定子电流i_s或定子电流的时间导数di_s/dt，它们可由转子磁链的估计值Ψ_r，根据异步电机的数学模型被重构出来，形成它们的估计值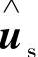、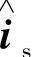或d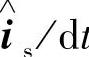。这样实测值和估计值之差通过与其相应的误差校正矩阵G构成转子磁链观测器的误差校正环节。

在具体实现时，根据实际需要，只取一项误差反馈即可。通过对误差校正矩阵G的合理选择，可以有效地配置状态观测器的极点，从而达到改善观测器稳定性、加快状态估计的收敛速度以及提高抗干扰的鲁棒性等目的，因而误差校正矩阵G在这种观测器中所起的作用是相当重要的。下面，将以电流模型法转子磁链观测器为例，讨论这种观测器的设计特点。

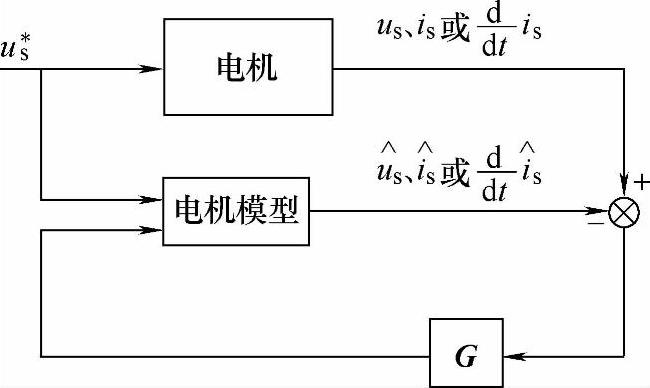
图4-24 基于误差反馈的转子磁链观测器原理

在分析异步电机转子磁链观测方法时，通常采用以定子电流、转子磁链为状态变量的状态方程，写成矢量形式，记作

式中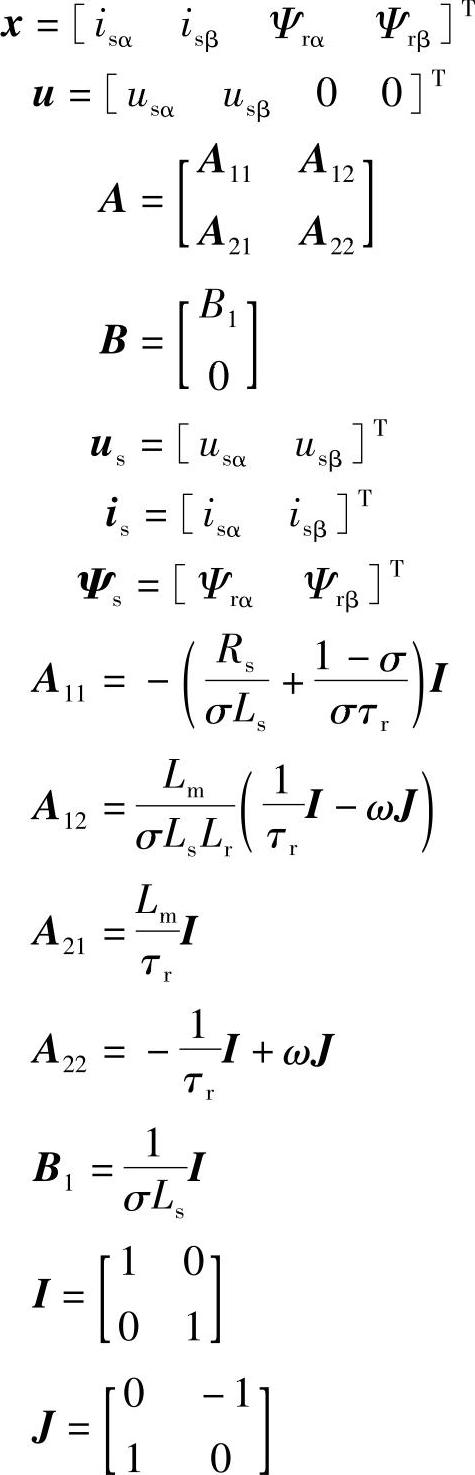定子电流的微分方程为

从该式相应地可以得到i_s和u_s的表达式为(www.daowen.com)

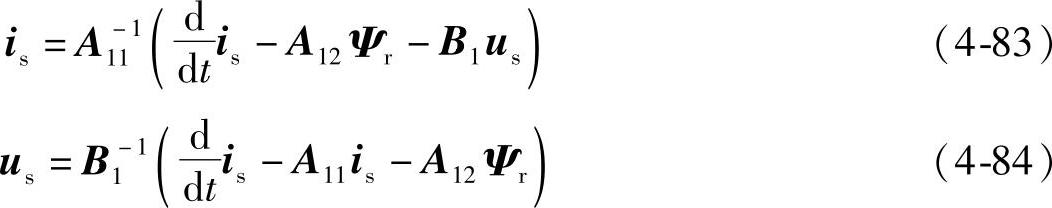
由式（4-82）～式（4-84）可以得到与其相应的估计值表达式为

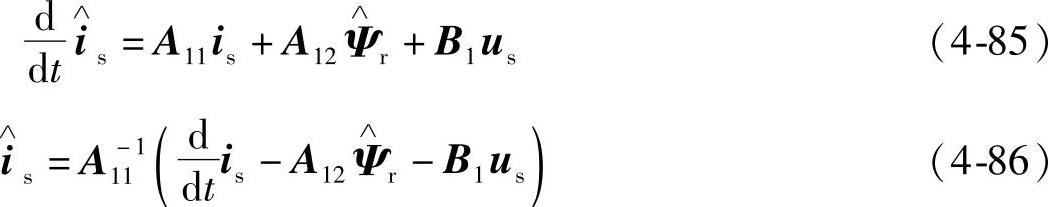
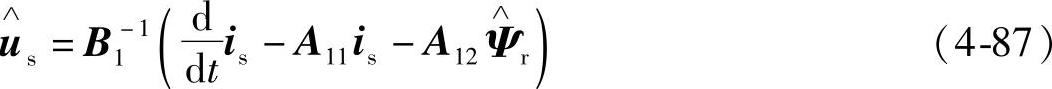
式（4-82）～式（4-84）分别与式（4-85）～式（4-87）相减可得

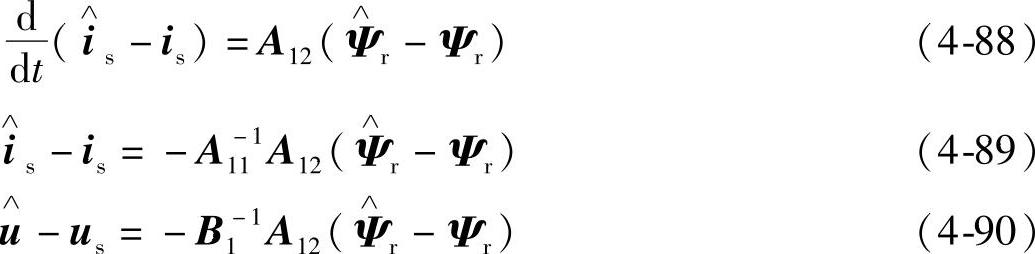
式（4-88）～式（4-90）给出了定子电流时间导数、定子电流和定子电压的误差表达式。基于误差反馈的转子磁链观测器表达式可写为

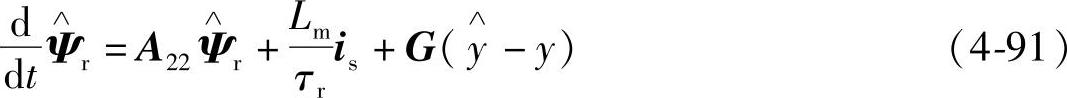
式中，y代表di_s/dt、i_s、u_s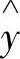；代表d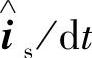、、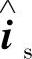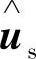。因A₁₁为对角矩阵，且其对角元素相等，故从式（4-88）～式（4-90）可以看出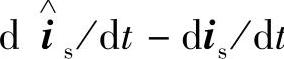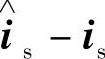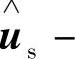，、、u_s之间的差异仅表现在比例系数上，因此从状态观测器设计角度来看，三者是一致的。

这里，以电流误差反馈为例设计转子磁链观测器，将式（4-89）代入式（4_-91）得

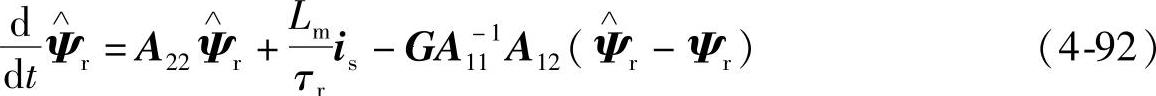
式（4-92）即为基于定子电流误差反馈的转子磁链观测器的表达式，它的状态估计误差为

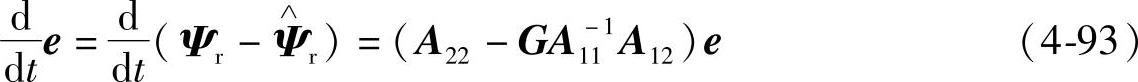
根据A₁₁、A₁₂、A22的表达式，可将式（4-93）整理为

式中，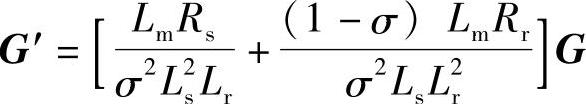

这样，状态估计的收敛特性完全取决于矩阵（I-G′）A₂₂的特征根分布，同时矩阵A₂₂为二阶满秩矩阵，状态观测器的极点可以通过选择误差校正矩阵G（或G′）的元素来任意配置，从而保证能获得优良动态特性和收敛特性的状态观测器。为简单起见，设

将式（4-95）代入式（4-94）得

式中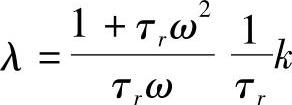，（k为常数）。

显然，状态估计的收敛特性取决于λ的选择。一般情况下，按λ=10/τ_r来确定误差校正矩阵G，可以保证状态观测器具备应用的快速收敛能力，并同时对噪声有一定的抑制能力；过大的λ往往会导致状态观测器抗噪声干扰能力的下降。

下面推导基于电流误差反馈的转子磁链观测器的实现方法。求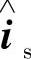的式（4-86）中存在导数项di_s/dt，为了消除导数带来的影响，可引入辅助变量Z。

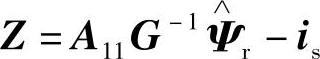
由此可得

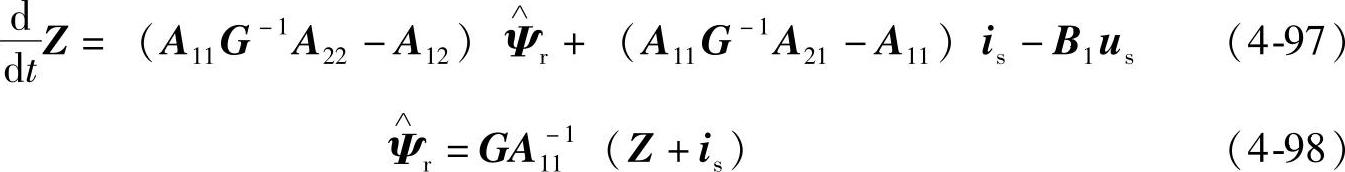
式（4-97）和式（4-98）就构成了基于电流误差反馈的异步电机转子磁链观测器，其运算框图如图4-27所示。

以上给出了基于定子电流误差反馈的转子磁链观测器的设计方法，同理可根据需要设计分别基于定子电压误差反馈和定子电流时间导数误差反馈的转子磁链观测器。我们认为，与开环观测模型相比，这种状态观测器存在收敛速度和估计精度可以直接控制的特点，如果电机参数和转速均能保证有较高的测量精度，那么它可以达到较高的估计精度，同时也具备理想的收敛速度。然而，当电机参数和转速存在较大测量偏差时，必须在收敛速度和估计精度之间进行折中，从这种意义上进，基于误差反馈的转子磁链观测器对来自电机参数变化等干扰的鲁棒性没有得到显著的提高。

（2）基于龙贝格状态观测器理论的异步电机全阶状态观测器 上述各种观测器属于异步电机降阶状态观测器的范畴，因为它仅对转子磁链Ψ进行估计，而对其他状态变量（如定子电流）未作估计。由于信号检测噪声是不可避免的，而普通的降阶状态观测器对定子电流检测中含有的噪声往往是无能为力的，从而削弱了降阶状态观测器的抗干扰能力。然而，这个问题在全阶状态观测器中是可以解决的，因为对可检测变量进行估计相当于引入了一个状态滤波器，使状态观测器对来自状态检测噪声的干扰具有较强的鲁棒性。下面将简单讨论全阶状态观测器的设计原理，其设计方法与前述降阶观测器的设计相类似，这里只做一简单介绍。

异步电机状态方程式依然记作式（4-81），为

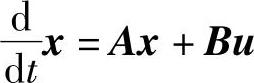
并令输出方程为

利用系统输入u和输出Y等可直接检测的信息，为其设计一状态观测器如下：

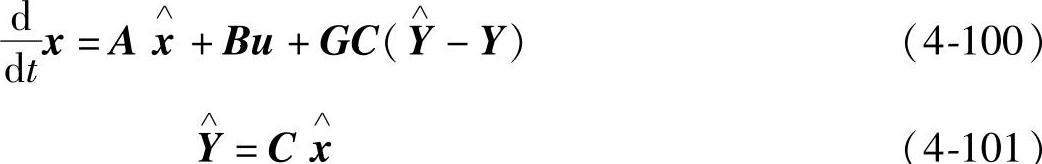
将式（4-100）减去式（4-101）可得状态估计动态误差方程如下：

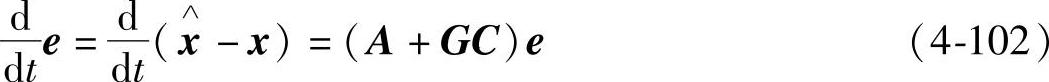
根据龙贝格状态观测器理论可以证明，对于线性定常系统，若（A，C）能观，则矩阵（A+GC）的特征值，即状态观测器的极点可以任意配置，因而可通过选择适当的G矩阵保证x绝对收敛于x。虽然这是针对线性定常系统提出的，但它的设计思想同样适用于异步电机状态估计，图4-25给出了龙贝格状态观测器原理图。

以上简单叙述了异步电机的龙贝格全阶状态观测器设计原理。有兴趣的读者可参与有关自动控制理论的书籍，了解详细的证明推导过程和观测器设计方法。总的来说，全阶状态观测器在稳定性，动、静态收敛特性，以及抗参数变化和测量噪声干扰的鲁棒性方面都有了明显的改善，只是观测器的构成比较复杂，增加了控制系统的复杂性。

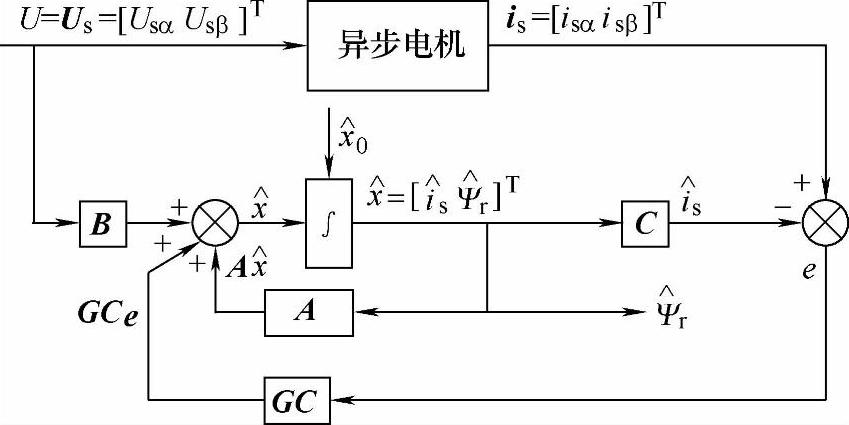
图4-25 龙贝格状态观测器原理图

（3）基于参数模型自适应理论的转子磁链观测器 当电机参数发生变化或转速测量偏差较大时，虽然误差反馈可以削弱它们对状态估计的动、静态收敛特性的影响，但由于对这些参数变化缺乏适应性，其鲁棒性仍不能尽如人意。

从理论上讲，解决以上问题最直接和最有效的手段是对电机的参数或转速进行在线辨识，即采用具有参数自适应能力的状态观测器来估计电机的转子磁链，由于这牵涉到参数辨识和速度辨识，在本章的其他小节中将有详细叙述，这里不再一一阐述，读者可参看4.5节。

小结：本节中介绍了转子磁链观测器的开环、闭环观测模型，并针对各自的特点及设计方法进行了讨论。从矢量控制的角度来看，为实现高性能，转子磁链观测器设计应满足以下几点要求：

1）估计算法是稳定的。

2）估计值对实际值的收敛速度要尽可能的快。

3）对受控对象参数变化和测量噪声应具有较好的鲁棒性。

4）实现起来要尽可能方便，结构上不过于复杂。

现有的观测器模型都不能同时满足以上几点要求，但又都有各自的适用范围。因此，根据实际需要，采取何种观测模型，需进行全面的折中考虑。