正弦PWM一般随着大功率电力电子器件开关频率的提高会得到很好的性能，因此在中小功率电机控制系统中被广泛采用。但对于大功率电力电子变流装置来说，太高的开关频率会导致大的开关损耗，因此是不可取的。况且大功率电力电子器件，如GTO晶闸管的开关频率目前还不能做得很高，在这种情况下，优化PWM技术正好符合需要。优化PWM即根据某一额定目标将所有工作频率范围内的开关角度预先计算出来，然后通过查表或其他方式输出，形成PWM波形。由于每个周期只有可数的几次开关动作，因此开关角度的小的变化对谐波含量影响很大。一般采用大型计算机在整个工作频率范围内寻优，计算出一个周期内实现某一特定目标所有开关角度，并去除可能的局部优化结果，因此是非常费时的，难以实现动态控制。目前均采取存表方式，然后通过少量插值计算或通过近似简化计算的方法来输出PWM波形。随着微处理器计算速度的提高，也有实时计算优化波形方案的出现^[16]。

1.谐波消除法

事实上，早在20世纪60年代初，人们就发现，在方波电压中加几次开关动作，可大大消弱某次特定的低次谐波，如3、5、7次等，从而使输出的电流波形非常接近正弦波^[11]。这种方法在20世纪70年代被Patel和Hoft采用傅里叶分析的方法所推广，从理论上证明了消除任意次谐波的可能性，但受大功率电力电子器件开关频率的限制，一般只把影响系统性能的低次谐波消除掉^[12]。这种方法中，基波电压可以超过进线电压，因此电压利用率很高。此外，还可以用有限的开关频率实现系统的高性能，因此它在大功率或电流型逆变器中应用较多。其主要缺点是实时控制困难，并且高次谐波的幅值大大增加，这会引起损耗增加。

2.效率最优PWM

人们过去认为，谐波消除法会自动实现系统的高性能，但理论分析表明，此法并没自动导致效率最优和转矩脉动最小^[14]。事实上，消除谐波法有两个解，即基波幅值可正可负，如

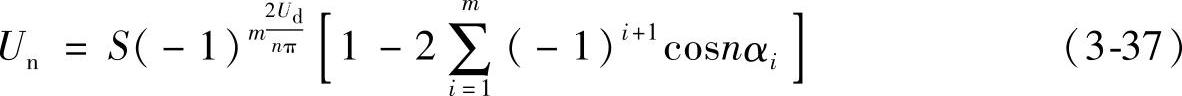
式中，S代表符号，可取正或负，均可消除同样的谐波，但得到的PWM波形却大不一样，如图3-22所示。理论分析表明，图3-22b所示PWM模式更接近效率最优PWM。因为效率是和负载大小有关的，因此在求解效率最优PWM的过程中，应考虑电机和负载的不同，但结果表明，这种不同造成的影响可忽略不计[14]。在用数

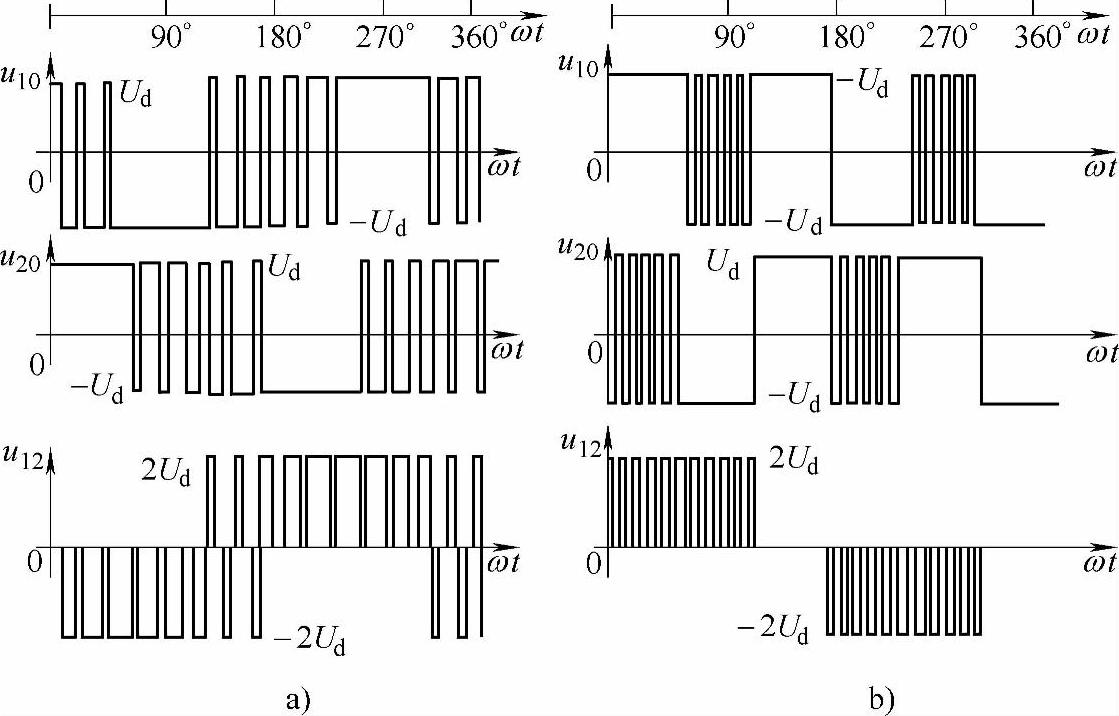
图3-22 最优PWM波形

a）消除谐波PWM b）效率最优PWM

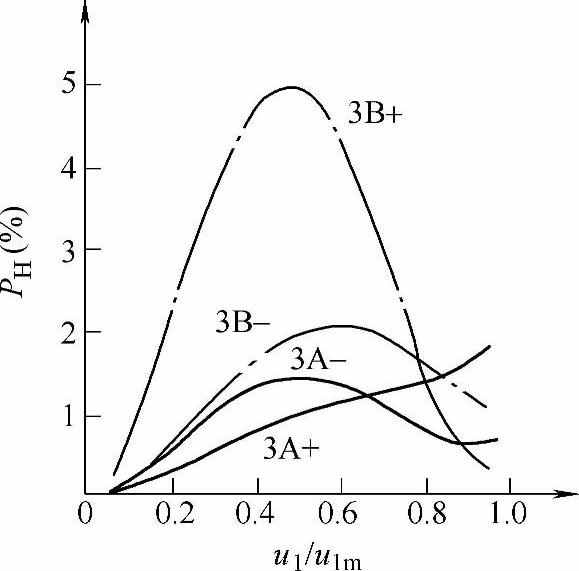
字计算机求解最优化PWM时，初始点的选择非常重要，并且由于局部最优化的存在，需要计算所有的开关角度才能将其剔除。在参考文献[14]中，计算了开关角度为3个和5个时的所有导致效率最优的PWM模式，分别得到4个和8个全局最优结果，并且在电压从零到额定范围内变化时，每个优化PWM模式作用的区段是不同的。因此，在整个电压范围内，效率最优PWM的开关角度不是连续变化的，当开关角度为3个时的4个最优结果如图3-23所示，这几乎是所有优化PWM的共同特征。

3.转矩脉动最小PWM

根据同样的方法，F.C.Zach还计算了实现转矩脉动最小的优化PWM模式。对于开关角为3个的情况，得出6组最优PWM模式，3组对应基波电压为正，3组对应基波电压为负。对应电压为正时的两组PWM波形如图3-24所示。

(www.daowen.com)

图3-23 效率最优PWM的开关角度

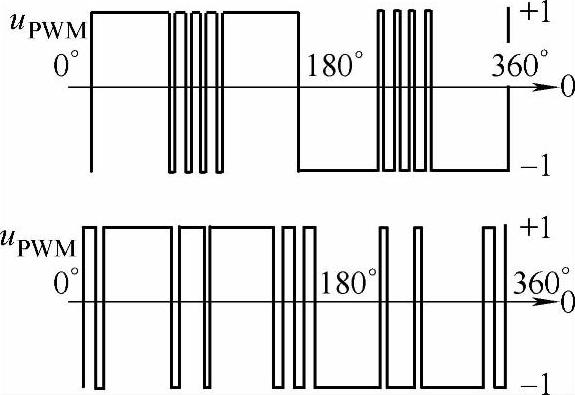
图3-24 转矩脉动最小PWM波形

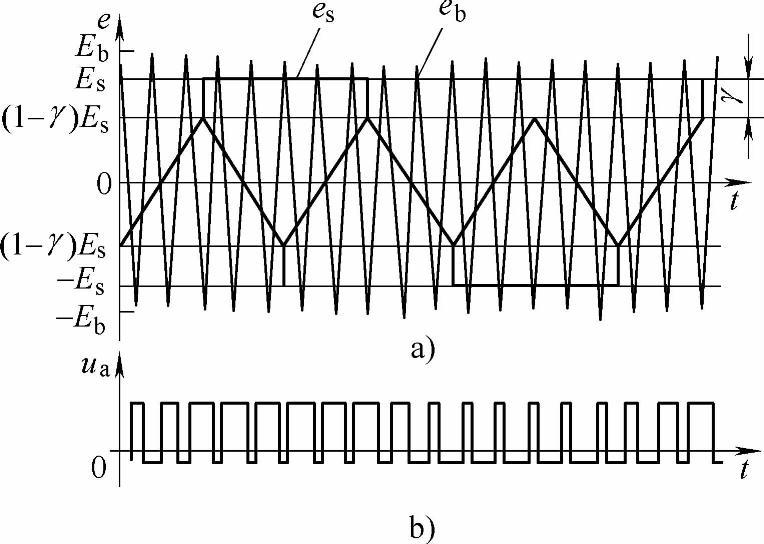
图3-25 转矩脉动为零PWM波形

a）调制波形 b）PWM波形

值得一提的是，Taniguchi^[15]证明了消除转矩脉动的有效方法并不是将逆变器所有的谐波都去掉，只要满足u₅/u₇=5/7这一条件，即可使对低速特性影响最大的6次转矩脉动等于零。此外，他还从理论上证明，当用过调制的梯形波代替正弦波时，可以降低开关频率，并且有几个特殊的波形满足局部最优条件，即可实现转矩脉动为零（见图3-25）。此时系统调压只能采取在直流侧加斩波器的方法来实现。

实际上，上述最优PWM技术的概念是由G.S.Buja和G.B.Indri于1977年在参考文献[13]中提出来的。不过，那里的目标函数既不是低次谐波，也不是效率或转矩脉动，而是所有谐波电流的有效值，即

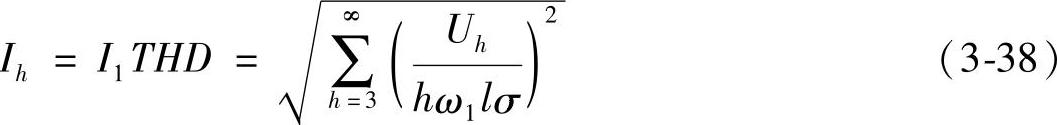
参考文献[13]中计算了开关角度分别为1、2、3、4时的最优PWM模式，成为优化PWM的经典结果，并一再被各国学者所引用和进一步的研究。图3-26给出开关角度为4时的优化PWM模式角度分布，从这里我们再次看到，优化PWM在整个电压范围内的不连续性。

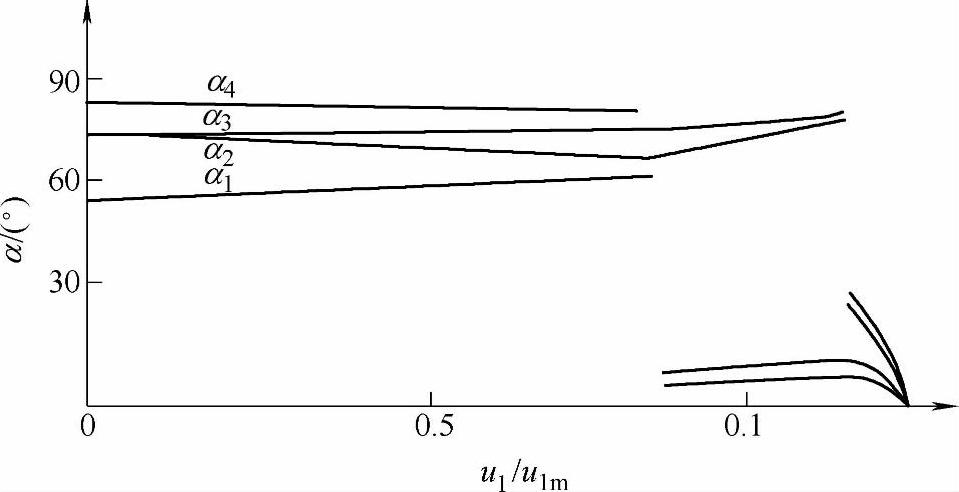
图3-26 优化PWM模式角度分布

目前，随着计算机技术的发展，人们期待已久的优化PWM模式的实时完成将成为现实^[16]。