磁通SPWM（即SVPWM）和电压SPWM不同，它是从电机的角度出发的，着眼于如何使电机获得幅值恒定的圆形旋转磁场，即正弦磁通^[5]。它以三相对称正弦电压供电时交流电机的理想磁通圆为基准，用逆变器不同的开关模式所产生的实际磁通去逼近基准圆磁通，并由它们比较的结果决定逆变器的开关状态，形成PWM波形。由于该控制方法把逆变器和电机看成一个整体来处理，所得模型简单，便于微处理器实时控制，并具有转矩脉动小、噪声低、电压利用率高的优点，因此目前无论在开环调速系统或闭环控制系统中均得到广泛应用。

1.磁通SPWM原理

电机的理想供电电压为三相正弦，其表达式如下：

按照合成电压矢量的定义（由Park变换）：

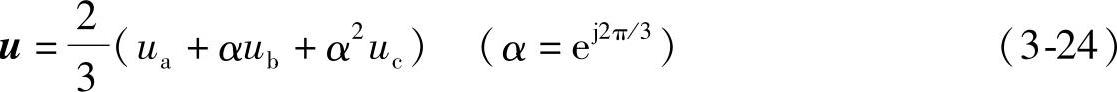
将式（3-23）代入式（3-24）中，得到理想供电电压下的电机空间电压合成矢量

u=U_me^-jωt （3-25）

理想情况下，空间电压矢量为圆形旋转矢量，而磁通为电压的时间积分，也是圆形的旋转矢量。现在我们观察逆变器的输出情况。图3-11为逆变器的简化的拓扑图，并定义三个开关函数S_a，S_b，S_c，当S（a，b，c）=1代表上半桥臂导通，当S（a，b，c）=0代表下半桥臂导通。对于180°导通型逆变器来说，三相桥臂的开关只有8个导通状态，包括6个非零矢量和2个零矢量。在忽略定子电阻压降时，对应6个非零矢量磁通的运动轨迹为六边形。此时磁通的大小和旋转的角速度都是变化的，从而引起转矩脉动、电机损耗等现象。这种控制方法可用于对调速精度要求不高的场合，如1985年Depenbrock教授提出的直接转矩控制系统中一直采用此方法控制磁通。

目前，磁通SPWM多采用控制电压矢量的导通时间的方法，用尽可能多的多边形磁通轨迹逼近理想的圆形磁通。具体方法有两种：一是磁通开环方式，即三矢量合成法磁通正弦PWM，二是磁通闭环方式，即比较判断法磁通SPWM。将逆变器输出的8种电压矢量用式（3-24）的空间电压矢量来表示得到如图3-12所示的结果。

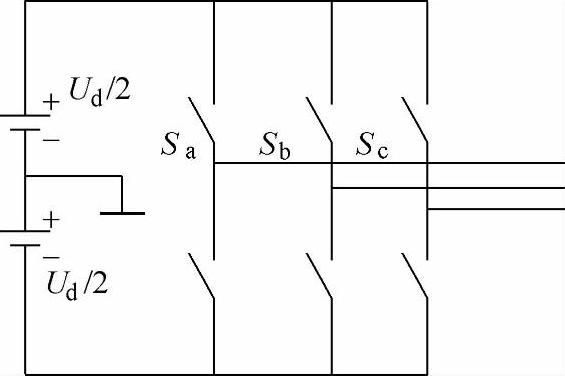
图3-11三 相逆变桥

S（a，b，c）=1时上管导通；S（a，b，c）=0时下管导通

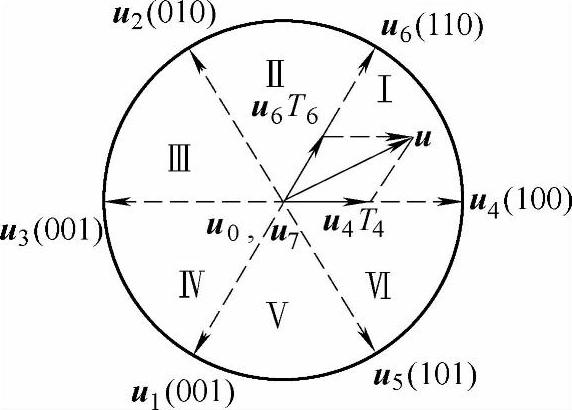
图3-12 电压矢量图

为了使逆变器输出的电压矢量接近圆形，并最终获得圆形的旋转磁通，必须利用逆变器的输出电压的时间组合，形成多边形电压矢量轨迹，使之更加接近圆形。这就是正弦PWM原理的基本出发点。例如：当旋转磁通位于图3-12所示的Ⅰ区时，用最近的电压矢量合成，并按照伏秒平衡的原则，得

T₆u₆+T₄u₄+T₀u₀=Tu （3-26）式中，T_n为对应电压矢量u_n的作用时间；T为采样周期；u为合成电压矢量。

2.磁通轨迹控制

由上述原理出发，要有效地控制磁通轨迹，必须解决三个问题：

1）如何选择电压矢量。

2）如何确定每个电压矢量的作用时间。

3）如何确定每个电压矢量的作用次序。

对于第一个问题，通常将圆平面分成6个扇区，并选择相邻的两个电压矢量用于合成每个扇区内的任意电压矢量。对于第二个问题，即每个电压矢量的作用时间，由以下公式导出（以扇区Ⅰ为例）：

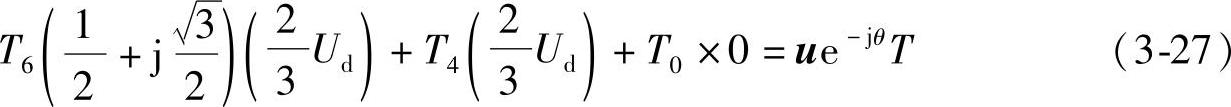
令式（3-27）等号两边实部、虚部相等，得到以下结果：

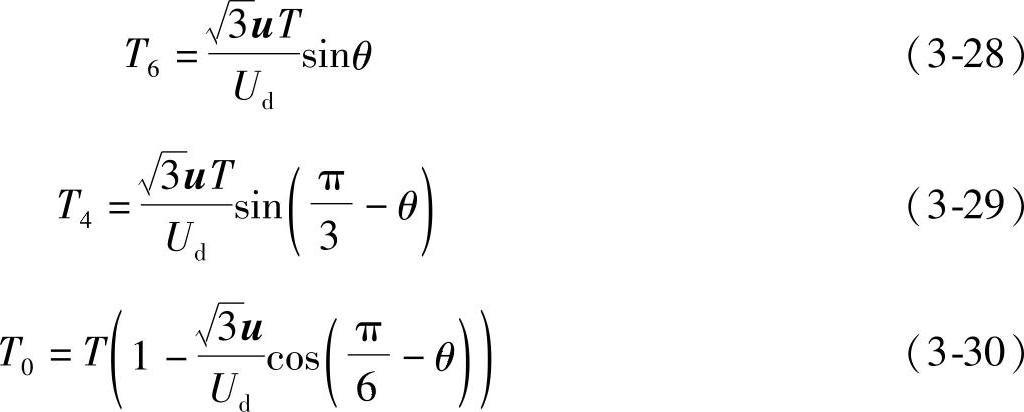
其中，0≤θ≤π/3；并设零矢量u₀与u₇的作用时间分别为T₀₀=（1-k）T₀；T₀₇=kT₀。

各电压矢量的作用次序要遵守以下的原则：任意一次电压矢量的变化只能有一个桥臂的开关器件工作，表现在二进制矢量表示中只有一位变化。这是因为如果允许有两个或三个桥臂开关器件同时工作，则在线电压的半周期内会出现反极性的电压脉冲，产生反向转矩，引起转矩脉动和电磁噪声。下面以Ⅰ扇区为例介绍七段式SVPWM波形的产生方法（见图3-13）。

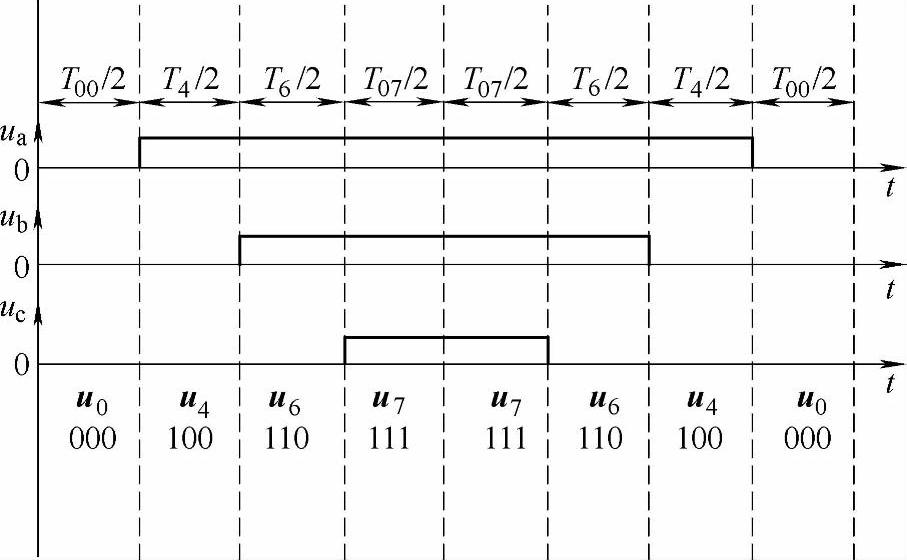
图3-13 七段式SVPWM波形

3.SVPWM与其他PWM的比较

由式（3-28）～式（3-30）可以得出：随着合成电压矢量u的长度增加，T₁、T₂也逐渐加大，T₀逐渐减小。但是为了满足u在线性区内的要求，必须使T₀非负，即

要使θ在任何情况下，式（3-31）总成立，则

可见相电压u的幅值达到上限时，输出线电压的基波峰值为U_d，它比SPWM的高15.47%（常规SPWM在满调制（m=1）时，输出的线电压幅值为0.866U_d）。在这一点上，和前述准优化PWM有异曲同工之处。下面将推导出SVPWM在实质上也是一种带谐波注入的调制方法。

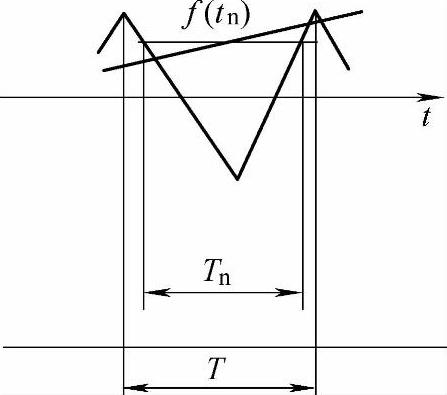
从SPWM的规则采样法出发，可以导出SVPWM的隐含调制函数。采用规则采样法（见图3-14）时，脉宽为

式中，U_rm为三角波幅值。

(www.daowen.com)

图3-14 规则采样法

在已知T_n的情况下，可以由式（3-33）求出f（t_n），以U_rm归一化表示时有

同理，根据SVPWM所输出的脉宽，也可以得到SVPWM的隐含调制波。例如，根据图3-13中的各个扇区的波形以及式（3-34），可以得到各个扇区的调制波，在0°到90°的一相隐含调制函数如下：

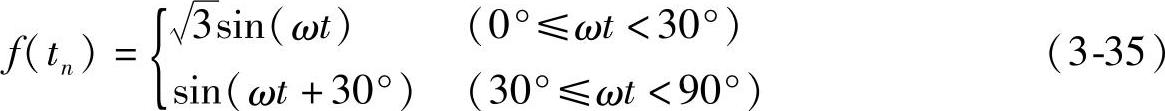
为了便于分析，也可求得隐含调制函数在整个2π内三相统一表达式为

u_a，b，c^**=u_a，b，c^*+u_z （3-36）式中

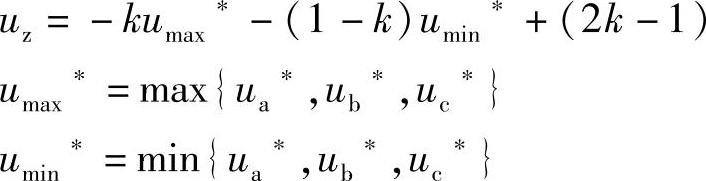
式中，m为调制比（这里的m的定义以半桥逆变器为参考，等于调制波基波的峰值与直流电压的一半之比）。图3-15给出输出基波为50Hz时A相u^**、u^*、u_z的波形。B、C两相的波形与之类似，只是滞后或超前120°。图3-16是不同k值时的零序分量波形，零序分量的波动频率是变换器输出基波频率的三倍，且可能含有直流分量（当k=0.5时不包含直流分量）。同时，零序分量不仅含有奇次谐波，还含有偶次谐波。

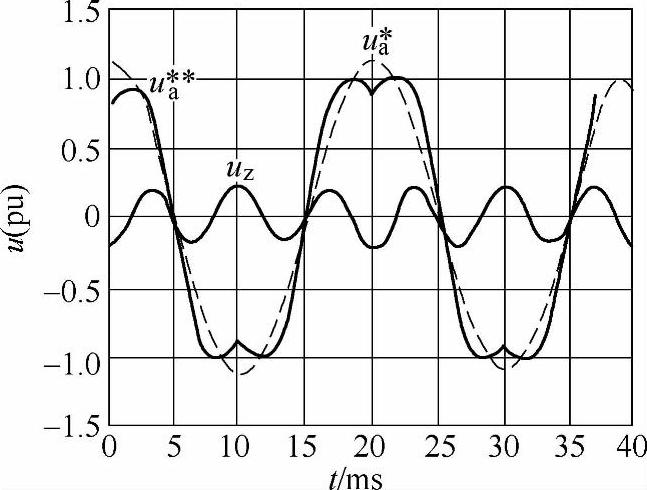
图3-15 u_a^**、u_a^*、u_z的波形（m=1.1547，k=0.5）

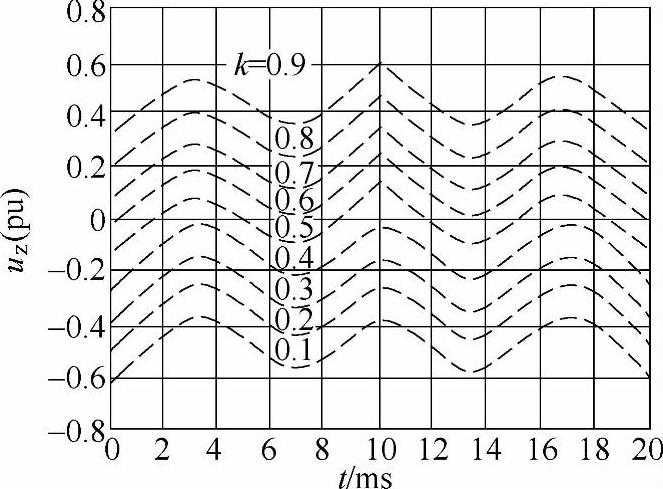
图3-16 不同k值时的零序分量（m=0.5，k=0.1～0.9）

从图3-15可以看出，零序分量的加入使得调制波的峰值拉低。当满调制（m=1.1547）时，调制波的基波峰值正好等于1。由于零序分量的加入，相调制波已经不是正弦波，所以输出相电压必有明显的畸变。相对于三相无中线系统，零序电压不会产生电流，而输出线电压因零序分量相互抵消仍保持正弦。所以，三相△联结负载时不会产生畸变谐波。

如果三相变换器为联结，负载上实际的相电压仍没有畸变。为说明问题，用理想电压源代表三相变流器。如图3-17所示，根据叠加原理，变流器可以等效为图3-17b和图3-17c的和。对图3-17b所示的基波受控源，负载中n₁点与直流侧中0点等电位。对于图3-17c所示的零序受控源，由于三相电压相等，故不产生电流。虽然没有电流，但零序电压u_z使负载中n₂点与零序电压相等。因此，总的负载中点电位（φ_n1+φ_n2）和直流侧中点的电位不相等，而是跟踪零序电压浮动，所以负载上的相电压仍然是正弦的。相电压的畸变只是指相对直流侧中0点而言的。

从上述分析及图3-15可以看出，SVPWM的调制波相当于在原正弦波上叠加了一个零序分量（当k=0.5时为三次谐波）。理论分析表明，SVPWM具有如下优点：

1）输出电压比正弦波调制时提高15%。

2）谐波电流有效值的总和接近优化。

图3-17 理想电压源

4.不连续脉宽调制

PWM的基本思想是通过提高开关频率，使谐波分量尽量向高频段移动，然后通过较小的滤波器滤除高频谐波。但是，提高开关频率带来了不容忽视的开关损耗。不连续脉宽调制是一种频率不太高，而谐波又比较小的调制方法。

不连续脉宽调制（Discontinuous PWM）也称为死区带PWM（Dead band PWM）或母线钳位PWM（Bus clamp PWM）。其基本思想是，通过在调制波中加入零序分量，使调制波在一段时间内等于三角载波的正峰值或负峰值，并且使三角波与调制波没有交点，于是开关状态保持不变。尽管产生不连续调制波的方法很多，但总体来说，调制波要精心设计，其规律性不强。SVPWM不仅可以将不连续调制与连续调制统一起来，而且提供了一种有规律的不连续调制方法。图3-18和图3-19分别表示了当k值为0和1时的三相调制波形、调制波基波波形和零序分量。这种调制方式通常也称为线电压调制。

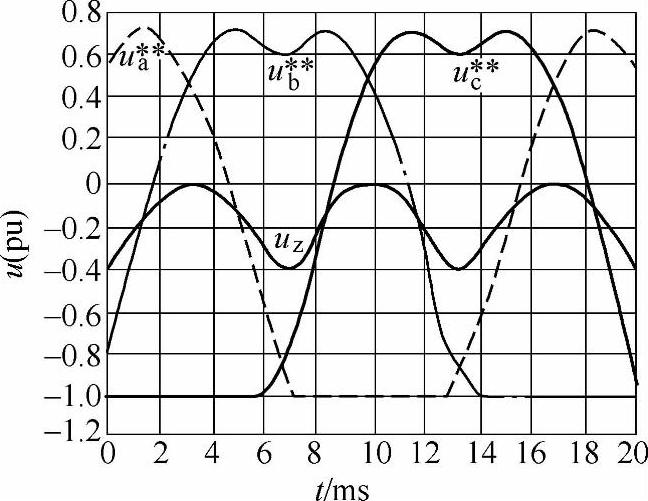
图3-18 k=0的调制波（m=1.0）

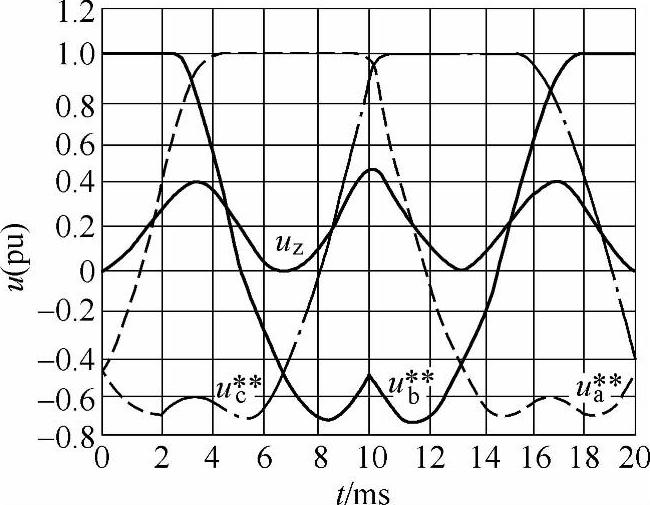
图3-19 k=1的调制波（m=1.0）

当k为0或1时，每相的调制波有连续的1/3周期维持为直流母线的正极或负极电位。由于载波和调制波没有交点，所以这段时间内对应的桥臂开关状态不变。对照图3-13所示的开关波形，进一步说明，当k逐渐减小时，矢量u₇的作用时间减小，而矢量u₀的作用时间加长，其结果是各相脉宽逐步减小，到k=0时，u₇完全没有作用，则扇区中脉宽最窄的那一相脉宽为零。反之，当k值逐渐增大时，矢量u₀的作用减小，而u₇的作用加大。图3-18与图3-19中，输出的相电压波形有120°为正母线电压或负母线电压，三相桥臂各有120°不动作，所以开关损耗比连续调制时降低33%。

如果在不同的扇区，让k值交替地等于0或1，那么将得到正负半周对称的各60°不动作的PWM波形。图3-20a、b是两种不同情况下的调制波。TI公司的DSP芯片中的SVPWM功能，就是按图3-20的方式进行调制的。可以发现，图3-20的两个负半波60°正是图3-19中的120°不动作区的前60°和后60°。k值的切换点决定了开关状态固定区域的起始点与终止点。图3-20中调制波虽然在正负各60°时间相同，但波形的对称度差。将k值的切换点改为扇区的中点，可以得到对称的调制波。图3-21是k值在扇区中点切换时的调制波形。变化k值的切换点可以在一定的范围内控制开关器件的不动作区在一个周期内的具体位置。利用这一点还可以进一步降低开关损耗。

图3-20 k值在扇区边沿切换时的调制波[m=1.0，k=1（0°～60°）]

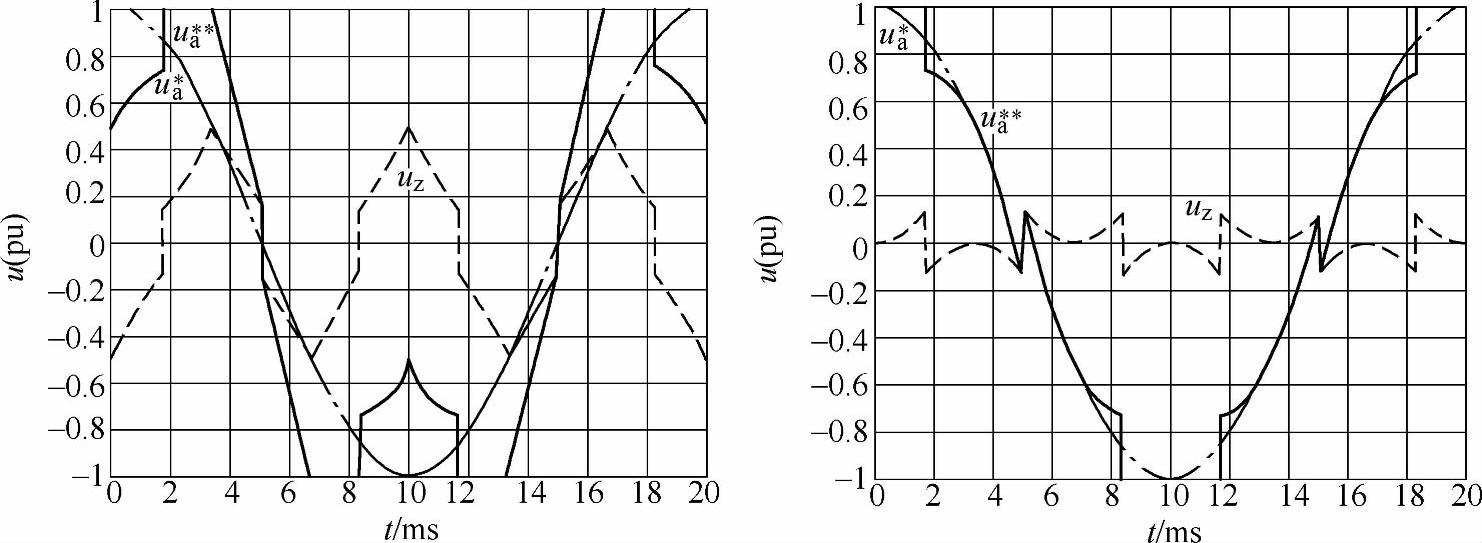
图3-21 k值在扇区中点切换时的调制波[m=1，k=1（-30°～30°）]

因为开关损耗和开关频率、母线电压、线电流成比例。母线电压和开关频率是恒定的，而线电流为幅值变化的正弦波，所以在不同的时刻，开关器件上的瞬时损耗是不一样的。电流大时，开关损耗也大。如果通过k值的控制，使每半周的60°开关器件不动作区位于电流峰值的两侧对称分布，这对开关损耗的降低就十分明显。不连续脉宽调制的主要优点在于有效地降低开关损耗，尤其在高频工作时，该优点更加突出。由此可以得出，SVPWM实质上也是一种带谐波注入的规则采样PWM。对零矢量的不同处理方法，可以获得灵活多样的输出波形。

在某些要求无音频噪声的场合，如果用连续调制，则开关频率必须大于20kHz。而事实上，由于开关频率很高，电流谐波已经不是主要问题，而开关损耗的问题变得突出。如果用不连续调制，开关频率只需13kHz就能消除音频噪声。

5.闭环磁通PWM

因为在低速时定子电阻的影响变大，如果仍采用固定时间内顺序给出矢量的办法，则不能保证磁通轨迹的形状和大小。另外，零矢量的引入也造成磁通轨迹的畸变，使其幅值下降，系统带负载能力下降。在磁通开环系统中，往往通过函数发生器的方式进行补偿，但效果有时不很理想。事实上，最有效的方法乃是引入磁通的反馈，通过闭环的方式来控制磁通的大小和变化速度。闭环实现的方法可以是PI调节器，也可以用无差拍（Deadbeat）方式来比较估算磁通。并根据误差决定所施加的下一个电压矢量来形成PWM波形。这种方法适用于高性能变频器或调速系统，如直接转矩控制系统。其控制性能在很大程度上取决于磁通观测的准确性，在低速时，定子电阻、开关器件的导通压降、逆变器互锁时间的影响都应考虑在内。为了更有效地改善低速磁通和电流的波形，又提出了矢量合成法和叠加补偿法等，有效地抑制了电机的脉动和噪声。