如前所述，电压SPWM技术可以由模拟电路、数字电路或大规模集成电路芯片来实现。采用模拟电路时，由振荡器分别产生正弦波和三角波信号，然后通过比较器来确定逆变器某一桥臂开关器件的开通和关断。这种传统的做法，使系统的器件过多，控制线路复杂，控制精度也难以保证。目前，由于微处理器的速度和精度在不断提高，数字化PWM方法发展迅速，典型的有自然采样和规则采样PWM两种方法^[2]。在数字化PWM方法中，三角波和正弦波的交点时刻可转化为一个采样周期内对输出脉冲宽度时间及间隙时间的计算，由计算机来完成，时间的改变可通过定时器来完成。自然采样PWM虽可真实地反映上述控制规律，但是脉冲宽度

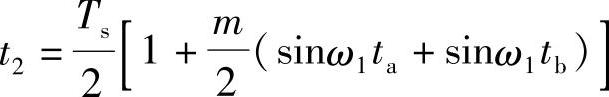
是一个超越方程，需要计算机迭代求解，难以用于实时控制。当然也可以把事先计算出的数据放在计算机内存中，利用查表的方法输出PWM波形。但频率范围变化很大时，将占用大量内存。规则采样PWM是对自然采样的简单近似，此时脉冲宽度为

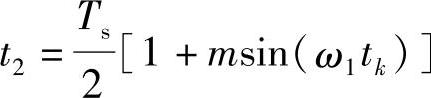
或

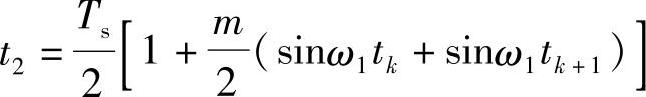
但此时的t_k、t_k+1为已知，因此可用计算机快速计算出每相的脉宽和间隙时间。(www.daowen.com)

规则采样PWM具有实现容易、控制线性度好等优点，但它和自然采样PWM一样，具有电压利用率低（输出电压的有效值只能达到进线电压的0.864倍）的缺点。为了解决这一问题，S·R·Bowes等人又于1985年提出了准优化PWM技术^[3]和用于高压高频的准优化PWM（HVSOPWM）技术。Bowes等人通过对优化PWM的详细研究，发现了它的基本特征，并以此为依据，确定了一个特殊的调制函数，对优化PWM进行近似。在规则采样PWM中，调制函数为正弦波，而准优化PWM的调制波为基波和3次谐波的叠加，其数学表达式为

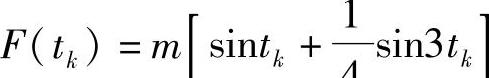
式中，t_k=KT_s/2。加3次谐波后，调制比m和输出电压之间的关系仍为线性，但由于3次谐波将基波的峰值削平，因此只有当m达到1.2时，才可能出现过调制（见图3-9）。因此，电压利用率相当于提高了20%，达到1以上。当m﹥1.2时，出现过调制，控制规律不再是线性的，谐波也无法被优化。为了保证从PWM波形到方波之间的连续过渡，并具有准优化PWM的特征，又提出了HVSOPWM方法。根据优化PWM（例如消除谐波法）随着电压基波幅值升高，开关角的分布逐渐向边缘移动这一特点，HVSOPWM采用两级调制的方法，第一级先将采样信号加以预调制，使其分布向边缘移动，这样做的结果导致，在半个基波周期的中间的范围内将没有调制，而在边缘的调制规律仍采用准优化PWM技术，最后得到的波形就非常接近优化PWM的波形了，这样就近似实现了优化PWM的实时控制。在实际应用中，可将准优化PWM和HVSOPWM混合使用，在低频、低压时采用准优化PWM，在高压高频时切换到HVSOPWM。

电压SPWM技术还有其他实现方法，如等面积法、大规模IC芯片连续移相法等，限于篇幅，这里不一一介绍了。

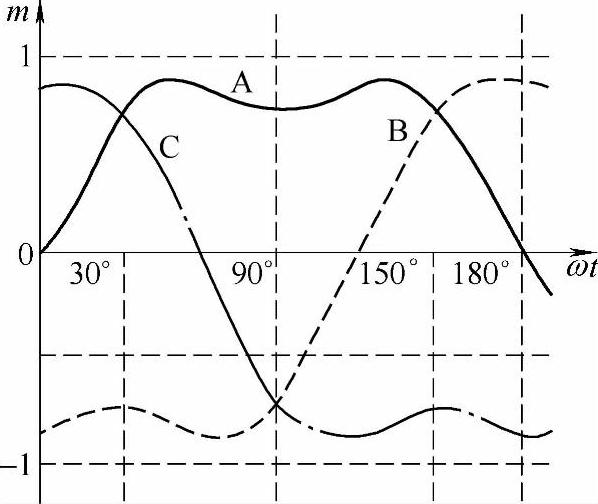
图3-9 优化的PWM调制波