本节研究在基频以下采用恒压频比带定子压降补偿的控制方式、基本保持磁通Φ_m恒定时的稳态机械特性，并探讨如何控制压频比才能获得更为理想的稳态性能。

1.恒压恒频时异步电机的机械特性

我们知道，当定子电压U_s和角频率ω_s都为恒定值时，异步电机的机械特性方程为

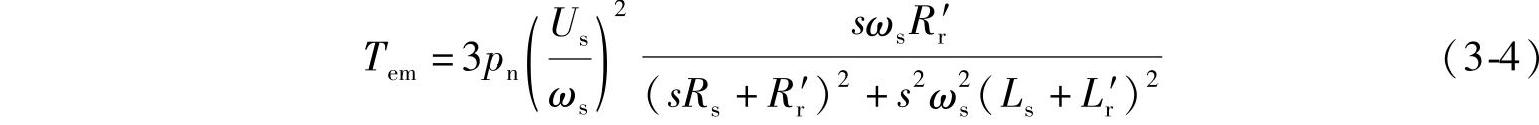
式中，p_n为异步电机极对数；s为转差率。

当s很小时，式（3-4）可以简化为

当s接近于1时，忽略式（3-4）中的分母R_r′时，则该式可以简化为

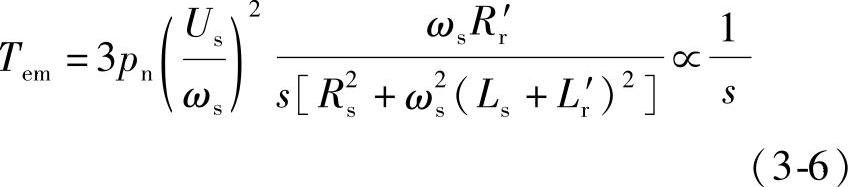
所以，在s很小时，转矩近似于s成正比；在s接近于1时，转矩近似与s成反比，可以得出机械特性如图3-5所示。

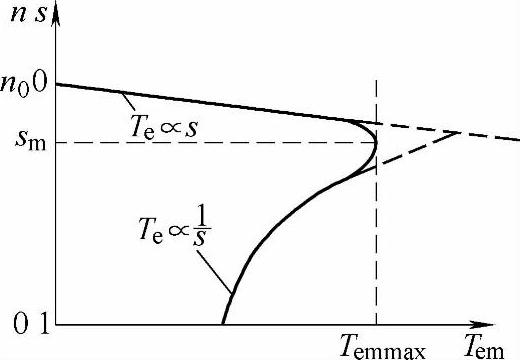
图3-5 恒压恒频异步电机的机械特性

2.电压、频率协调控制的机械特性

异步电机的稳态等效电路如图3-1所示。当异步电机带负载T_L稳定运行时，有

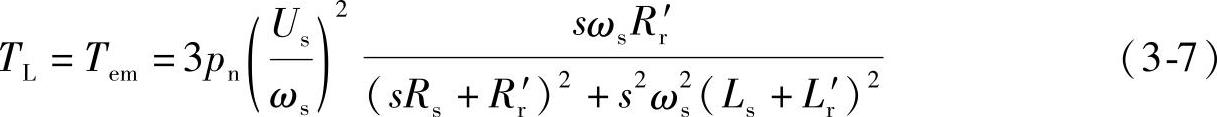
式（3-7）说明，当转速n和负载转矩T_L一定时，电压U_s和角频率ω_s可以有多种配合。在电压和频率的不同配合下，机械特性也是不同的，因此可以有不同方式的电压频率控制。下面分别讨论。

（1）恒U_s/ω_s控制 我们知道，为了近似保持气隙磁通Φ_m不变，在基频以下需采用恒压频比控制，此时同步转速也随之变化。同步转速为

因此，带负载时的转速降为

在式（3-5）所表示的机械特性的直线段上，可以导出

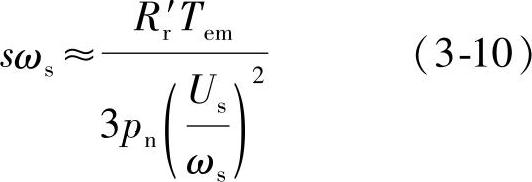
由此可见，当U_s/ω_s为恒值时，对于同一转矩T_em，sω_s是基本不变的，因而Δn也是基本不变的。这就是说，在恒压频比条件下改变频率时，机械特性基本上是平行下移的，如图3-6所示。(www.daowen.com)

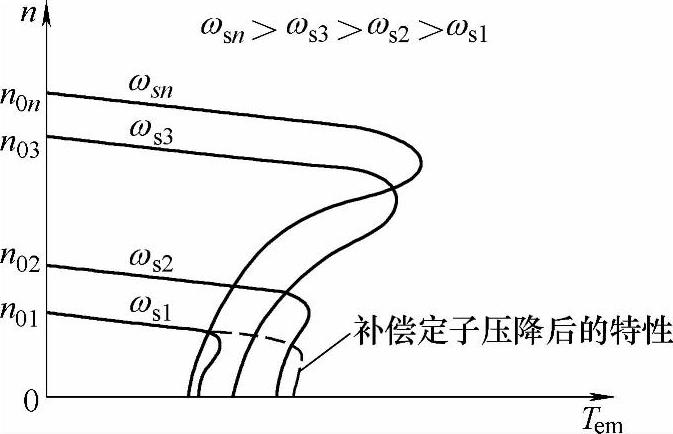
图3-6 恒压频比控制时变频调速的机械特性

另一方面，U_s/ω_s=恒值时，最大转矩T_emmax随角频率ω_s的变化关系为

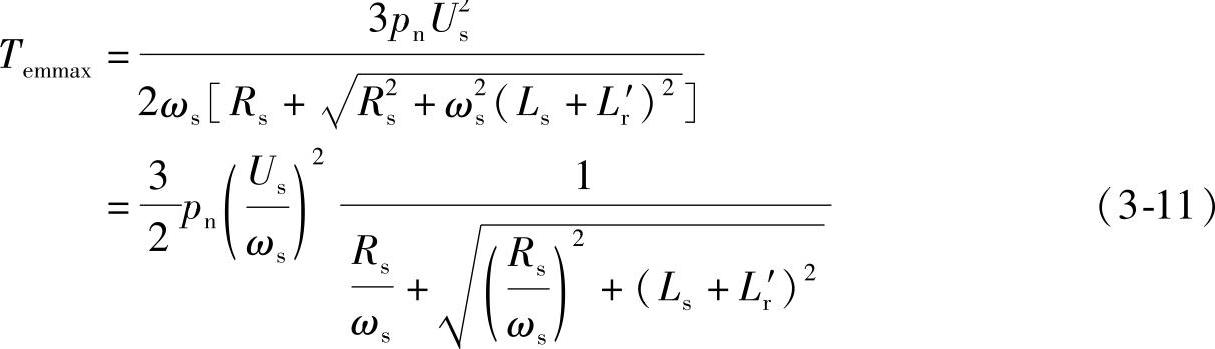
可以看出，最大转矩T_emmax随角频率ω_s的降低而减小，频率很低时，T_emmax太小将限制调速系统的负载能力，这时需要采用定子压降补偿，适当提高U_s可以提高负载能力。

（2）恒E_g/ω_s控制 如果在电压频率协调控制中，适当地提高电压U_s的份额，使它在克服定子压降以后，在基频以下能维持E_g/ω_s为恒值，则无论频率高低，每极磁通Φ_m均为常值。由图3-1所示的等效电路可看出

将上式代入电磁转矩基本关系式并整理得

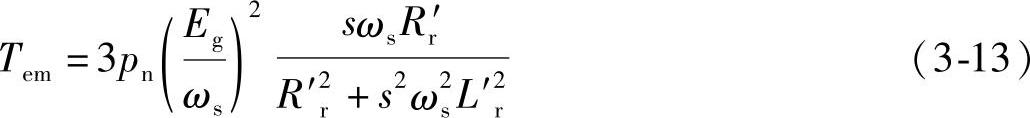
利用和以前同样的分析方法得到图3-7所示的机械特性。此时最大转矩为

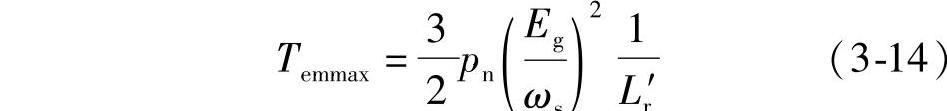
当E_g/ω_s为恒值时，T_emmax也为恒定，所以，恒E_g/ω_s控制的稳态性能是优于恒U_s/ω_s控制的。

（3）恒E_r/ω_s控制 如果把电压频率协调控制中的电压U_s相应地再提高一些，把转子漏抗上的压降也抵消掉，就得到恒E_r/ω_s控制。这时

将上式代入电磁转矩的基本关系式中，得

可以看出，这时的机械特性T_em=f（s）完全为一条直线，如图3-7所示。

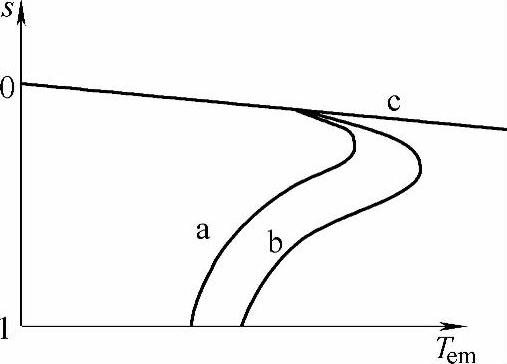
图3-7 不同电压-频率协调控制方式的机械特性

a—恒U_s/ω_s控 制b—恒E_g/ω_s控制 c—恒E_r/ω_s控制

如何控制变频装置的电压和频率才能获得恒定的E_r/ω_s呢？气隙磁通幅值是对应于它的旋转感应电动势E_g的，而与转子全磁通的幅值Φ_rm相对应的是E_r，因此只要能按照转子全磁通幅值Φ_rm=恒值进行控制，就可以获得恒定的E_r/ω_s。这也就是矢量控制理论的核心，关于矢量控制系统将在第4章中详细介绍。