在微机控制系统中，需要大量的数据处理工作，以满足控制系统的不同需要，由于各方面数据来源不同，有的是从A-D转换而得，有的则是直接输入的等，因而其数值范围不同，精度要求也不一致，表示方法各有差别，需要对这些数据进行一定的预处理和加工，才能满足控制的要求。

1.数据的表示方法

在用微机进行数据处理的过程中，用什么方法来表示被操作数，是提高运算精度和速度的一个重要问题。目前微机运算广泛采用的两种基本表达方法有定点数和浮点数。

（1）定点数和定点运算 定点数即小数占位置固定的数，可分为整数、纯小数和混合小数。其表示方法如下：

运算结果的小数点按如下规则确定：

在加减运算中，应遵循小数点对齐的原则，当两个操作数小数位相同，可直接运算，且小数位不变。当两个操作数的小数位不同，则需要通过移位的办法使小数位相同后进行运算。

在乘除运算中，若被乘（被除）数小数位为M，乘数（除数）的小数位为N，则结果的小数位为M+N（M-N）。

（2）浮点数和浮点运算 当程序中数值运算的工作量不大，并且参加运算的数的大小相差不大，采用定点运算一般可以满足需要，但定点数运算有以下两个明显缺陷：

●小数点的位置确定较为困难，需要一系列的繁杂处理。

●当操作数的范围较大时，不仅需要大幅度增加字长，占用较多的存储单元，且程序处理也较为复杂。

为有效处理大范围的各种复杂运算，提出浮点数和浮点运算。所谓浮点数是指尾数固定，小数点位置随指数的变化而浮动，其数学表达式为

±MC^E式中，M为尾数，是纯小数；E为阶码，是整数；C为底，对于微机而言，C=2。其中，尾数M和阶码E均以补码表示。如0.2×2³=1.6。

浮点数在存储单元中的一种表示方法如下：

可以根据运算精度要求来选择两字节尾数或三字节尾数来表示。

关于浮点数的运算，有许多现成的子程序，可直接拿来使用，这里不再介绍。但要说明的一点是，由于微机从外部获得的数大多为二进制数或二-十进制（BCD）码，所以在进行运算之前，必须将其转换为浮点数，而且要按一点的统一数据格式转换，称为浮点规格化，这一处理也有现成的实用子程序可以直接使用。

2.数字滤波程序的设计

电力电子系统的使用场合多为工业现场，干扰源很多，如电场、磁场、环境温度等等。在模拟系统中，为消除干扰，常常采用RC滤波，而在微机控制系统中，为减少采样值的干扰因素、提高系统的可靠性，常常采用数字滤波技术。

所谓数字滤波，是指通过一定的计算程序，对采样信号进行平滑加工，提高其有用信号，抑制或消除各种干扰和噪声。

数字滤波与模拟RC滤波相比，具有无需增加硬件设备、可靠性高、不存在阻抗匹配问题、可以多通道复用、可以对很低的频率进行滤波、可以灵活方便地修改滤波器的参数等特点。数字滤波的方法有很多，可根据不同的需要进行选择。下面介绍几种常用的数字滤波方法。

（1）程序判断滤波 程序判断滤波是根据生产经验，确定两次采样信号可能出现的最大偏差，若超过此偏差值，则表明该输入信号是干扰信号，应该除去，否则作为有效信号。

当采样信号由于外界电路设备的电磁干扰或误检测以及传感器异常而引起的严重失真时，均可采用此方法。

程序判断滤波根据其处理方法的不同，可分为限幅滤波和限速滤波两种。

限幅滤波：即将两次相邻采样值的增量绝对值与允许的最大差值进行比较，当小于或等于时，则本次采样值有效，否则应除去而代之以上次采样值。该法适用于缓变量的检测，其效果好坏的关键在于门限值的选择。

限速滤波：限速滤波的方法可表述如下：

设顺序采样时刻t₁、t₂、t₃所采集的参数分别为Y（1）、Y（2）、Y（3），那么

当|Y（2）-Y（1）|≤ΔY时，Y（2）输入计算机；

当|Y（2）-Y（1）|>ΔY时，Y（2）不采用，但仍保留，继续采样取得Y（3）；(www.daowen.com)

当|Y（3）-Y（2）|≤ΔY时，Y（3）输入计算机；

当|Y（3）-Y（2）|>ΔY时，则取[Y（2）+Y（3）]/2输出计算机。

限速滤波是一种折中方法，既照顾了采样的实时性，又顾及了被测量变化的连续性。但ΔY的确定必须根据现场的情况不断更新，同时不能反映采样点数N>3时各采样值受干扰的情况，因此其应用有一定的局限性。

（2）中值滤波 中值滤波是对某一参数连续采样N次（一般为奇数），然后依大小排序，取中间值作为本次采样值。

中值滤波对于去掉由于偶然因素引起的波动或采样器不稳定而造成的误差所引起的脉动干扰比较有效。若变量变化比较缓慢，采用中值滤波效果比较好，但对于快速变化过程的参数则不宜采用。

（3）算术平均值滤波 算术平均值滤波是要寻找一个Y（k），使该值与各采样值之间误差的二次方和为最小，即

由一元函数求极值原理，得

式中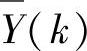，为第k次N个采样值的算术平均值；X（i）为第i次采样值；N为采样次数。

该方法主要用于对压力、流量等周期脉动的采样值进行平滑加工，但对于脉冲性干扰的平滑作用尚不理想。

（4）加权平均滤波 该方法是在算术平均值滤波的基础上，给各采样值赋予权重，即

且有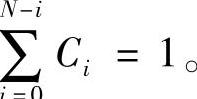

这种滤波方法可以根据需要突出信号的某一部分，抑制信号的另一部分。

（5）滑动平均值滤波 算术平均值滤波和加权平均滤波都需要连续采样N个数据，然后求得算术平均值或加权平均值，需要时间较长。为了克服这个缺点，可采用滑动平均值滤波法。即先在RAM中建立一个数据缓冲区，依顺序存放N次采样数据，每采进一个新数据，就将最早采集的那个数据丢掉，而后求包括新数据在内的N个数据的算术平均值或加权平均值。这样，每进行一次采样，就可计算出一个新的平均值，从而大大加快了数据处理的速度。

（6）RC低通数字滤波 前面讲的几种滤波方法基本上属于静态滤波，主要适用于变化过程比较快的参数，但对于慢速随机变量，采用短时间内连续求平均值的方法，其滤波效果往往不够理想。

为了提高滤波效果，可以仿照模拟RC滤波器的方法，如图1-21所示，用数字形式实现低通滤波。

模拟RC低通滤波器的传递函数为

式中，τ为RC滤波器的时间常数，τ=RC。由上式可以看出，RC低通滤波器实际上是一个一阶滞后的滤波系统。

图1-21 RC低通滤波器

将上式离散化，可得

式中，X（kT）为第k次采样值；Y（kT）为第k次滤波结构输出值；α为滤波平滑系数；α=1-e^-T/τ；T为采样周期。当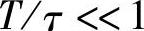时，α≈T/τ。

式（1-50）即为模拟RC低通滤波器的数字实现，可以用程序实现。

类似地，可以得到高通数字滤波器的离散表达式

Y（kT）=αX（kT）-（1-α）Y（kT-T）（1-51）

（7）复合数字滤波 为了进一步提高滤波效果，可以把两种或两种以上不同滤波功能的数字滤波器组合起来，组成复合数字滤波器（或称为多级数字滤波器）。

关于数字滤波器的编程，已有不少成熟的例子，读者可阅读相关参考文献[2]。