1.z变换的定义及表达式

连续信号e（t）的拉氏变换式E（s）是复变量s的代数函数。一个微分方程通过拉氏变换后可转化为s的代数方程，这样可大大简化运算。对计算机控制系统中的采样信号也可以进行拉氏变换。连续信号e（t）通过采样周期为T的理想采样后的采样信号e*（t）是一组加权理想脉冲序列，每一个采样时刻的脉冲强度等于该采样时刻的连续函数值，其表达式为

e*（t）=e（0）δ（t）+e（T）δ（t-T）+e（2T）δ（t-2T）+…（1-15）因为脉冲函数δ（t-kT）的拉氏变换为

L[δ（t-kT）]=e^-kTs所以式（1-15）的拉氏变换为

从上式中可明显看出，E*（s）是s的超越函数，因此用拉氏变换这一数学工具，无法使问题简化。为此，引入另一个复变量“z”，令z=e^Ts，代入式（1-16），得

上式是e*（t）的单边z变换。若上式中变量k是从-∞→+∞，则称为双边z变换。由于控制系统中研究的信号都是从研究时刻开始算起，即从t=0算起，所以使用的都是单边z变换，这里简称为z变换。

式（1-15）～式（1-17）在形式上完全相同，都是多项式之和，对应项的加权系数相等，在时域中的δ（t-T）、s域中的e^-Ts以及z域中的z^-1均表示信号延迟一拍。

在实际应用中，所遇到的采样信号的z变换幂级数在收敛域内都对应有一个闭合形式，其表达式是一个关于“z”的有理分式

若用zⁿ同除上式中的分子和分母，可得关于“z^-1”的有理分式，即

在讨论系统动态特性时，z变换式写成因子形式更为有用，即可写成

式中，z₁、…、z_m，p1、…、p_n分别是E（z）在z平面上的零点和极点。

z变换有一些重要性质，例如线性性质、平移定理、终值定理、初值定理等，利用这些性质能够方便地分析数字控制系统的稳定性、控制性能等，有兴趣的读者可阅读参考文献[1，3]。

2.求z变换的方法

（1）级数求和法 可利用式（1-15）～式（1-17）。

【例1-1】求指数函数f（t）=e^-t的z变换

解：f（t）的采样信号表达式为

f*（t）=1+e^-Tδ（t-T）+e^-2Tδ（t-2T）+e^-3Tδ（t-3T）+…

对应的拉氏变换式为

对应的z变换式为

（2）留数计算法 若已知连续时间函数f（t）的拉氏变换式F（s）及其全部极点s_i（i=1，2，…n），则f（t）对应的z变换为(www.daowen.com)

式中，r_i为多重极点s_i的阶数；m等于全部极点数与重复极点数之差。

（3）查表法 利用以上两种求取z变换的基本方法及z变换的性质，前人计算了大量时间函数所对应的z变换式，并列表供人使用。可以利用时域函数f（t）或其对应的拉氏变换F（s）进行查表，求得对应的z变换式。由于表内列写的函数有限，对于表内查不到的较复杂的原函数，常先把对应的拉氏变换式化成部分分式的形式，然后再查表。

3.z反变换

由z变换式E（z）求时域函数的过程称为z反变换。用“z^-1”符号表示，即

z^-1[E（z）]=e*（t）=e（kT）（k=0，1，2，…） （1-22）

注意，z变换式中只包含采样时刻信息，它和连续信号无一一对应关系，即z^-1[E（z）]≠e（t）。

由z变换式求时域信号有以下几种方法：

（1）幂级数展开式（长除法）若z变换式用幂级数形式表示，则很容易求得对应的时域函数。若已知z变换是多项式分式，可利用长除法求得时域函数。

【例1-2】求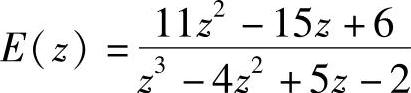对应的时域函数。

解：利用长除法

由z变换的定义知，时域函数为

e^*（t）=11δ（t-T）+29δ（t-2T）+67δ（t-3T）+145δ（t-4T）+…

（2）留数法z反变换为

时域函数可以利用E（z）z^n-1在E（z）的全部极点上的留数之和求得。若E（z）具有多重极点p_i，可以按照下式计算留数：

式中，r_i为多重极点p_i的阶次。

（3）查表法 若E（z）共有n个极点，除p₁是r重极点以外，其余均为互不相等的极点，E（z）可以化成部分分式之和，即

式中，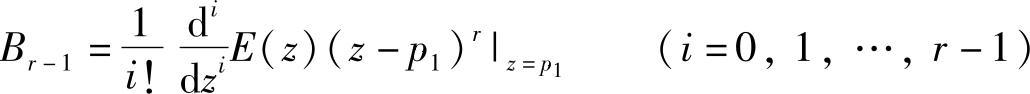

A_j=E（z）（z-p_j）|_z=p_j （j=2，3，…，n-r）

利用查表，可得各分式的反变换。