数字PID调节器是应用最普遍的一种控制规律，人们在大量的生产实践中，不断总结经验，不断改进，使得PID调节器性能日益提高，下面介绍几种数字PID调节器的改进算法。

1.积分分离PID调节器

系统中加入积分校正以后，会产生饱和效应，引起过大的超调量，这对高性能的控制系统是不允许的，引进积分分离算法，既可以保持积分的作用，又可减小超调量，使得控制性能有较大的改善。

积分分离算法要设置积分分离阈值E₀。

当|e（kT）|≤|E₀|时，也即偏差值|e（kT）|较小时，采用PID调节器，可保证系统的控制精度。

当|e（kT）|>|E₀|时，也即偏差值|e（kT）|较大时，采用PD调节器，可使超调量大幅度降低。积分分离PID调节器可表示为

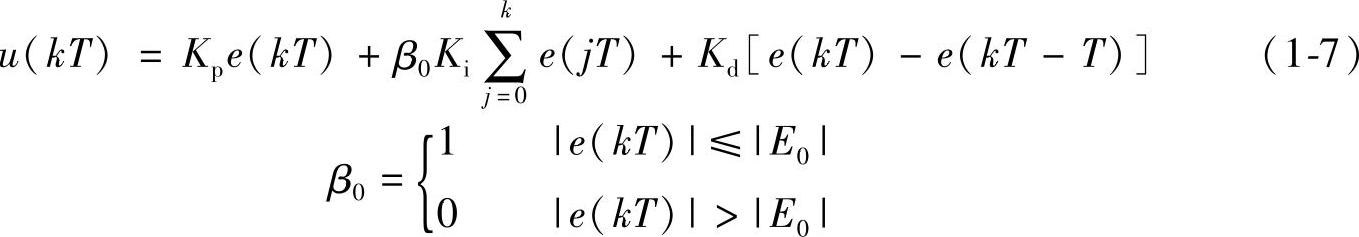
式中，β₀为逻辑系数。

采用积分分离PID调节器以后，控制效果如图1-5所示。由图可见，采用积分分离PID调节器后控制系统的性能确实有了较大的改善。

2.不完全微分PID调节器

通常大多采用PI调节器，而不采用PID调节器的原因是微分作用容易引进高频干扰。在数字调节器中，串接低通滤波器（如一阶惯性环节）可用来抑制高频干扰，因而可用来改善PID调节器抗高频干扰能力。一阶低通滤波器的传递函数为

不完全微分PID调节器如图1-6所示。

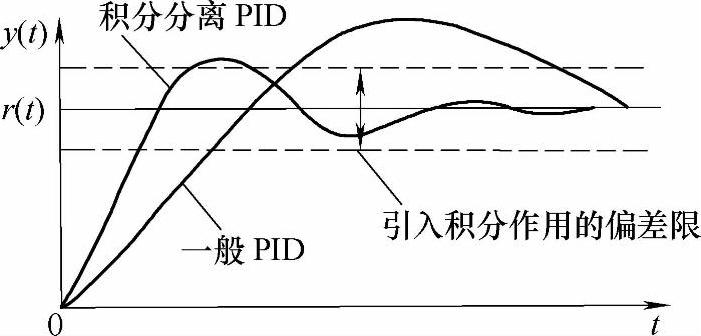
图1-5 积分分离PID控制的效果

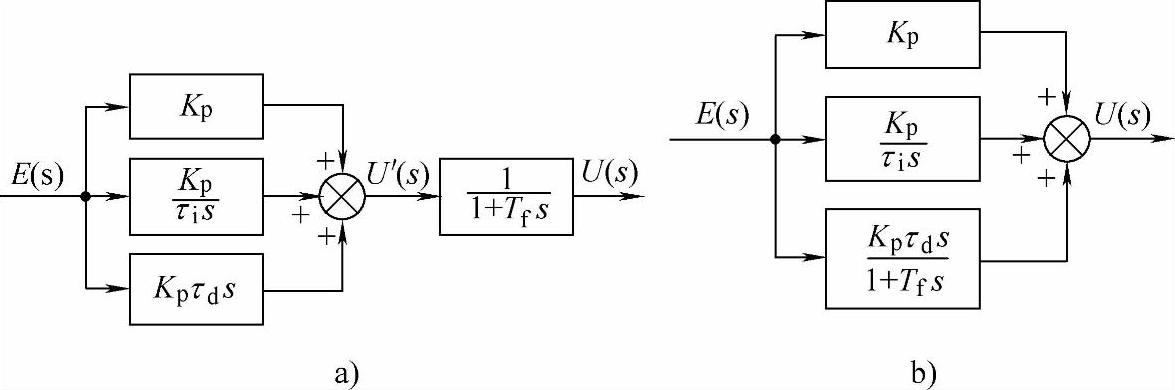
图1-6 不完全微分PID调节器

a）低通滤波器加在PID调节器之后 b）低通滤波器加在微分环节上

由控制原理图1-6a可得

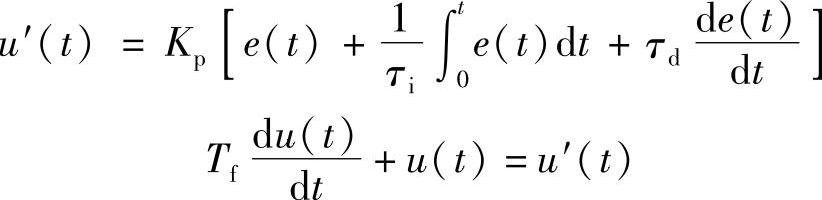
所以

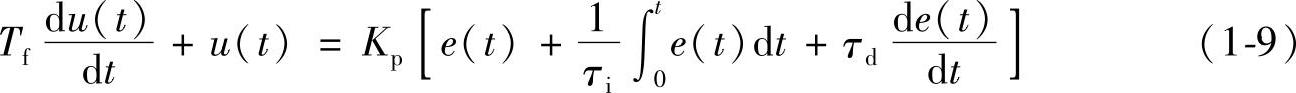
对式（1-9）离散化，可得差分方程

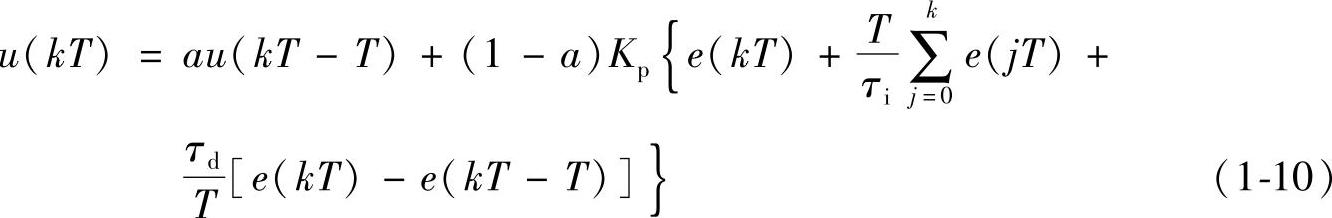
式中，a=T_f/（T+T_f）。

与普通PID调节器一样，不完全微分PID调节器也有增量式算法，即

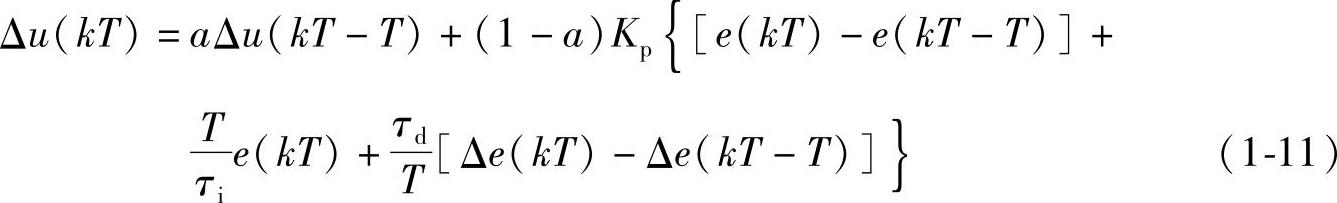
式中(www.daowen.com)

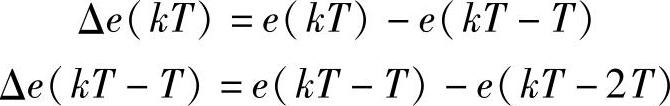
设数字微分调节器的输入为阶跃序列e（kT）=c，k=0，1，2，…，c为常值。当使用完全微分算法时

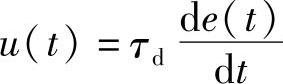
将上式离散化，可得

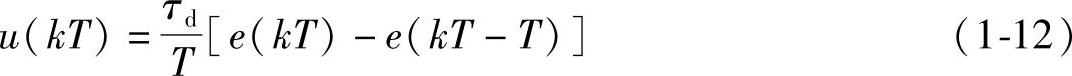
由式（1-12）可得

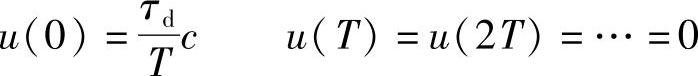
可见，普通数字PID调节器的微分作用只在第一个采样周期内起作用，不能按照偏差变化的趋势在整个调节过程中起作用。另外，通常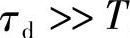。所以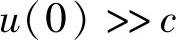，微分作用在第一个采样周期里作用很强，容易溢出。不完全微分数字PID调节器的引入不但能抑制高频干扰，而且能克服普通数字PID调节器的缺点，数字调节器输出的微分作用能在各个周期里按照偏差变化的趋势，均匀地输出，改善系统的性能。对其分析如下：

对数字微分调节器，当使用不完全微分算法时，有

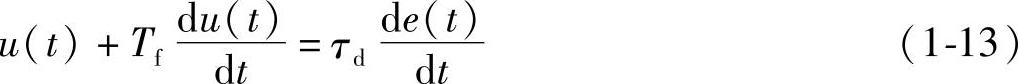
离散化后可得

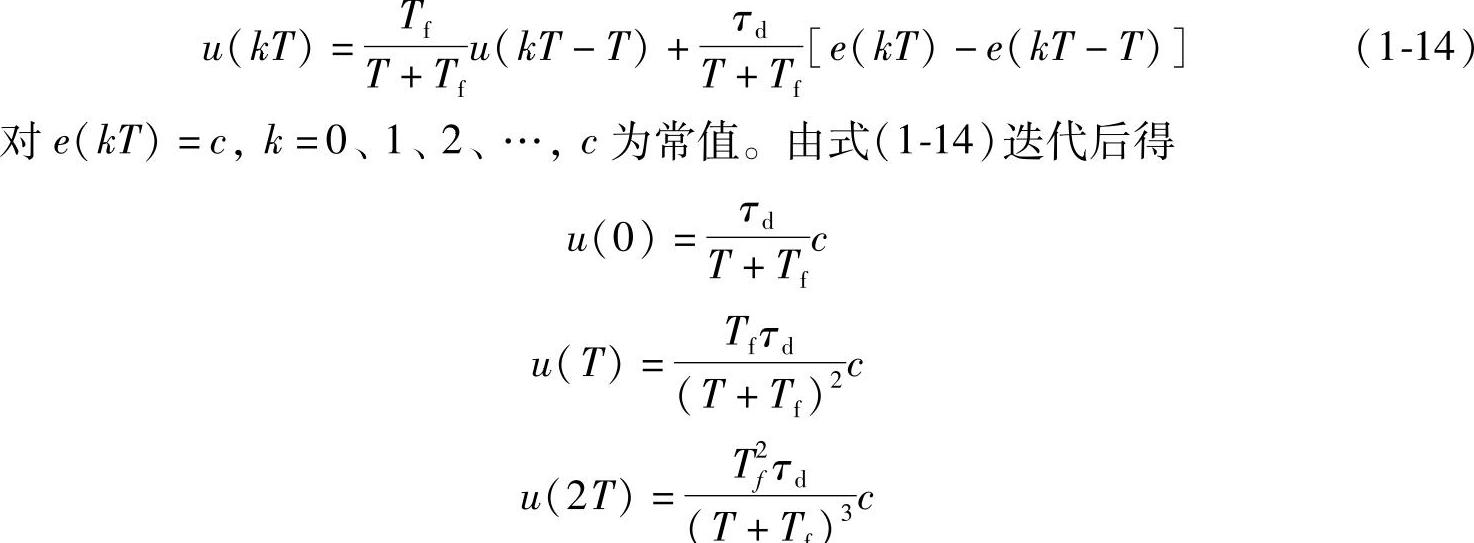
显然，u（kT）≠0；k=1，2，…；并且

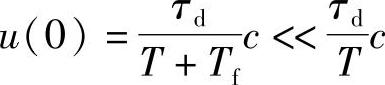
因此，在第一个采样周期里，不完全微分数字调节器的输出要比完全微分数字调节器的输出幅度小得多，具有比较理想的调节性能，所以尽管不完全微分PID调节器较之普通PID调节器的算法复杂，但仍然受到越来越广泛的重视和使用。

3.微分先行PID调节器

微分先行是把微分运算放在比较器附近。它有两种结构，如图1-7所示。图1_-7a是输出量微分，图1-7b是偏差微分。

输出量微分只对反馈值进行微分，而对给定值不作微分，这种输出量微分调节器适用于给定值频繁升降的场合，可以避免因升降给定值过于频繁而引起系统超调量过大和易产生剧烈振荡的缺点。

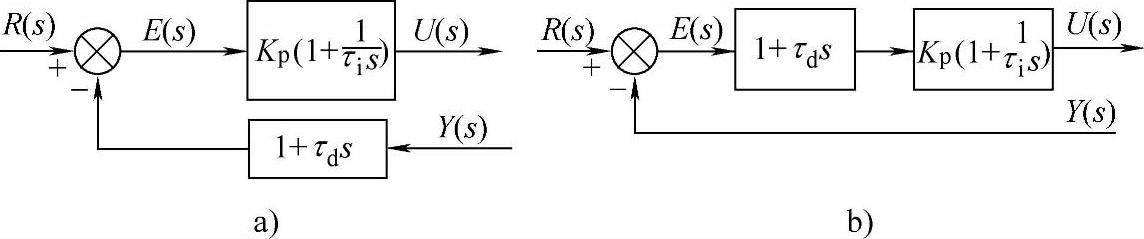
图1-7 微分先行PID调节器

a）输出量微分 b）偏差微分

偏差微分是对偏差值进行微分，也就是对给定值和反馈值都有微分作用。这种办法多用在矢量控制系统的内环控制调节器中。

4.带死区的PID调节器

在要求控制作用变动少的场合，可采用带死区的PID调节器，带死区的PID调节器实际上属于非线性控制的范畴，其结构如图1-8所示。相应的控制算法为当|e（kT）|≤|e₀|时，e′（kT）=0，PID调节器输出保持原状态。而当|e（kT）|>|e₀|时，e′（kT）经过PID调节器对控制系统进行调节。

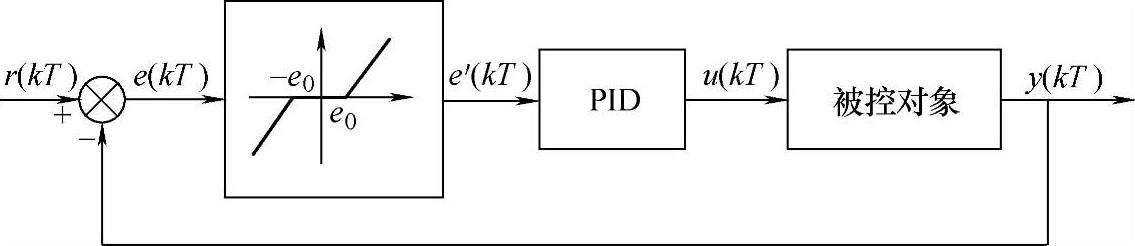
图1-8 带死区的PID调节器

值得注意的是，改进的PID调节器算法不需要增加硬件设备，只须根据控制对象对原有调节器算法进行适当改变，即可大大提高控制系统性能，体现了计算机数字控制系统的突出优点，因此，它的实际使用越来越多，而且还在不断发展。