在水冷技术中，热量主要通过强迫对流的方式进行传递。

1.圆管内强迫对流

圆管内流动时，流体边界层发展受到壁面限制，因此有流态和发展段的区别。三种流态分别是层流（Re＜2300）、过渡区（2300＜Re＜10000）与湍流（Re＞10000）。两个阶段是入口段与充分发展段。在充分发展段，流动沿轴向速度不变，其他方向速度为零，圆管速度分布为抛物线形分布。从进口到充分发展段之间的区域为入口段，热边界层薄，局部表面传热系数较高并沿主流方向下降。

（1）管内层流强迫对流传热关联式

管内层流强迫对流传热常用Sieder－Tate公式来计算其管道平均Nu：

式中，定性温度为流体平均温度，特征长度为管径，适用于Prf为0.48～16700，μf／μw为0.0044～9.75，Nuf≥3.72，管子为等壁温条件和入口段。

（2）管内湍流强迫对流传热关联式

对于管内液体的湍流强迫对流传热，有多个计算关联式。

Dittus－Boelter关联式为

式中，定性温度为流体平均温度，特征长度为管径，加热流体时n＝0.4，冷却流体时n＝0.3，适用于流体与壁面温度为中等温差的情况（水温差不超过20～30℃），Ref为104～1.2×105，Prf为0.7～120，l／d≥60。

Gnielinski关联式为

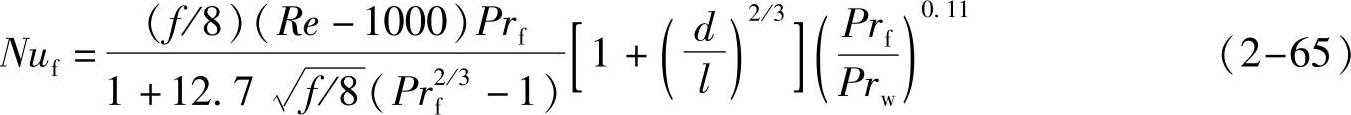
式中，l为管长，Prf／Prw为0.05～20。f为管内湍流流动的Darcy阻力系数，按Filonenko公式计算为

式中，Re为2300～106，Prf为0.6～105。

2.矩形直通道强迫对流传热

（1）矩形直通道内湍流强迫对流传热关联式

矩形直通道内湍流强迫对流传热与圆管内传热变化规律基本类似，可以采用式（2－64）和式（2－65）计算，但式中的特征长度有所不同。

对于矩形直通道，如图2－6b，其特征长度为

对于平行截面，a》b，则式（2－67）变为

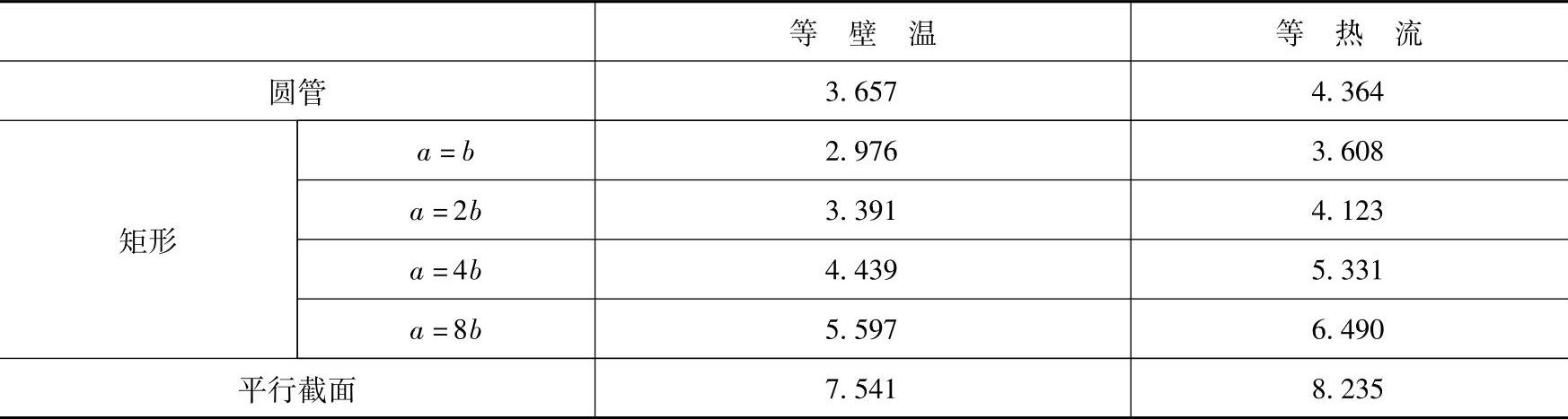
（2）矩形直通道内层流强迫对流传热关联式 矩形直通道内层流强迫对流传热与圆管内传热变化规律基本类似。对于不同截面形状和边界条件的通道内强迫对流层流传热，充分发展段的Nu见表2－6。

表2－6 层流充分发展段的Nu

（3）流体外掠平板强迫对流

当Ref＜5×105时（特征长度为平板长度l），流动处于层流状态，其传热关联式为

当5×105＜Ref＜107时，流动处于湍流状态，其传热关联式为

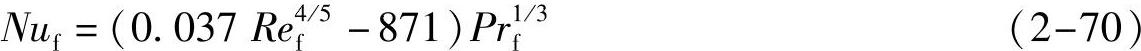
（4）混合对流现象

强迫对流与自然对流均需要考虑的对流传热称为混合对流。混合对流需要根据以下公式来判定：

(www.daowen.com)

当Gr／Re2≤0.01时，自然对流可以忽略；当Gr／Re2≥10时，强迫对流可以忽略；当0.01≤Gr／Re2≤10时，对流属于混合对流。混合对流传热需要根据自然对流与强迫对流方向等实验测定和拟合计算。

3.水冷板散热的测试计算模型

对于结构较为简单的水冷板散热器，可以采用热阻网络模拟直接计算，而复杂的水冷板散热器则需要采用数值模拟与实验测定方法确定。

类比电学的欧姆定律，基于水冷板壁面与主流温差，水冷板热阻R与电力电子器件热功率P的关系为

式中，Tw和Tf为器件表面与主流流体的温度，Tf＝（Tout＋Tin）／2

由牛顿冷却定理得整个水冷板的热功率为

式中，h为流体传热系数；A为水冷板换热面积

由式（2－72）与式（2－73）得

基于水冷板冷却液进出口温度的热阻Rth为

稳态情况下，假定热功率与冷却液的冷却功率平衡，则由冷却液热物理性能和进出口条件可计算热功率：

式中，W为质量流量；cp为比热。

由式（2－75）与式（2－76）得

由式（2－73）与式（2－76）得

4.热阻网络模型

对于结构较为简单的水冷板散热器，可以采用热阻网络模拟直接计算，而复杂的水冷板散热器则需要采用数值模拟与实验测定方法确定。

类比电学的欧姆定律，水冷板热阻R与电力电子器件热功率P的关系为

式中，ΔT为器件表面与主流流体的温差；q与S分别为热流密度和面积。

对于如图2－6b所示的单个通道结构，其热阻如图2－9所示。由图2－9可以求出单通道由壁面到流体传热的等效热阻R0。

对于矩形直通道水冷板散热器，由于不同通道换热基本类似，不同通道间的换热基本忽略，整个水冷板散热器热阻可以视为不同通道热阻的并联形式，如图2－10所示。如果边界通道散热也较大，则可以考虑边界热阻。

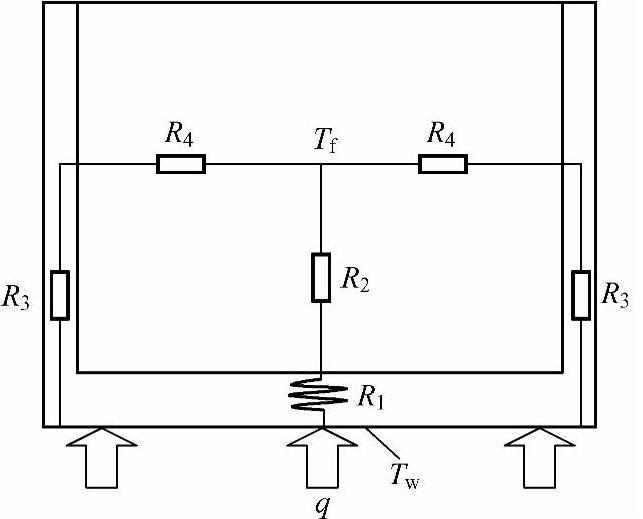
图2－9 单通道结构热阻

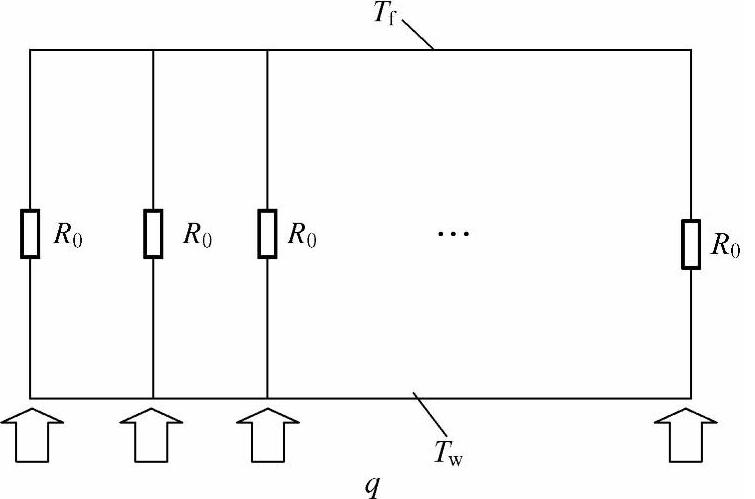
图2－10 矩形直通道热阻

对于S形直通道水冷板散热器，通道内流体间存在换热热阻R5，不同通道壁面存在热阻R6，此外流体主流温度和壁面温度随着流动不断升高，整个水冷板散热器热阻如图2－11所示。

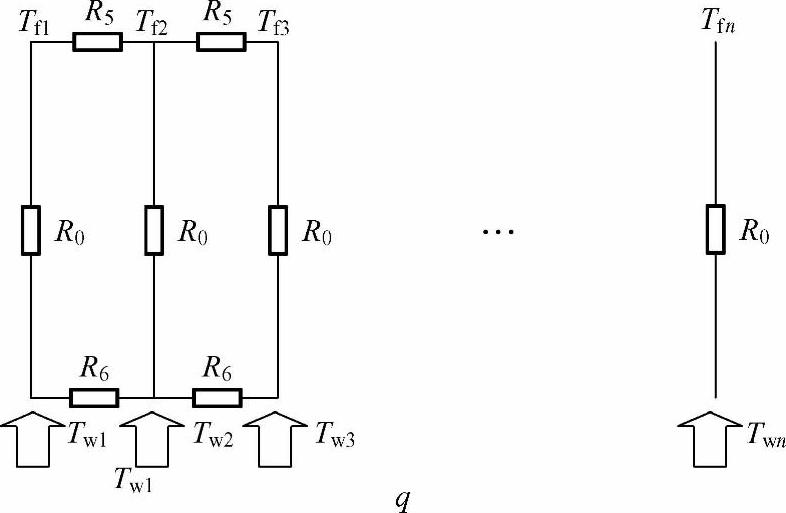
图2－11 S形直通道热阻