若仿壁虎机器人采用对角步态在光滑负表面进行黏附运动，当机器人由四只脚掌共同黏附变为只有对角的两只脚掌黏附时，受重力的影响，处于支撑状态的两只脚掌中每只脚掌的黏附力为四只脚掌共同支撑时每只脚掌黏附力的两倍，且仿壁虎机器人由两只对角脚掌与平面的分离开始，沿处于黏附状态脚掌所在的对角线产生一定角度的旋转，此时处于支撑相的脚掌为拉伸状态，仿壁虎机器人重心将略有降低。处于摆动相的脚掌执行落腿动作与目标面接触黏附时不能有效利用干黏附材料的法向黏附力，以下将对出现该现象的原因进行分析，并以提高脚掌黏附材料的利用效率及机器人的运动稳定性为目标，提出姿态调控方法。

仿壁虎机器人在运动过程中质心在竖直方向上的偏移与机器人脚趾结构有直接关系，机器人的脚趾为由PVC片基底和干黏附材料组成的弹性结构，机器人在光滑负表面进行稳定黏附运动时，其足端黏附模型如图8.4所示。当机器人四足都黏附在负表面上时，此时机器人脚趾根部与负表面的垂直距离记为z1，单只黏附脚掌的黏附状态如图8.4（a）所示；当机器人只有对角脚掌在负表面上时，此时机器人脚趾根部与负表面的垂直距离记为z2，单只脚掌的黏附状态如图8.4（b）所示。

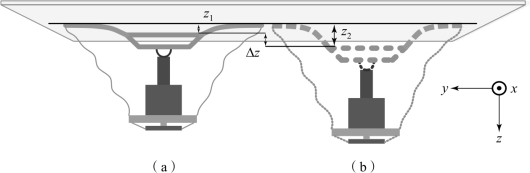
图8.4　脚掌黏附示意

（a）机器人四足都黏附在负表面上时，单只脚掌黏附状态；（b）对角脚掌在负表面上时，单只脚掌黏附状态

由于仿壁虎机器人由四足共同黏附支撑变为对角两足黏附支撑时，受重力影响，处于支撑相的足端脚趾承受重力变大，其脚趾发生形变增大，即其足端产生位移变化，该位移变化量记为Δz。将仿壁虎脚掌黏附模型等效为弹簧阻尼模型，对仿壁虎机器人进行被动柔顺控制，其足端法向黏附力变化量计算公式为：ΔF＝Kp1Δz+Kv1Δz˙，其中Δz为脚掌的位移变化量，Kp1为弹簧刚度系数，Kv1为阻尼系数。(www.daowen.com)

在仿壁虎机器人与接触平面交互时会产生碰撞，该碰撞力会导致机器人机身的震颤，同时也将导致机器人落腿过程中脚掌与接触面间的黏附效果不理想。为有效削弱仿壁虎机器人与接触平面交互时产生的碰撞力，现提出将仿壁虎机器人与接触面间的碰撞简化为弹簧阻尼模型，通过对仿壁虎机器人足端位移进行反馈控制实现对机器人足端碰撞力的主动柔顺控制。仿壁虎机器人足端与接触平面的模型如图8.5所示。该弹簧阻尼模型可表示为：fe＝Kp2 x+Kv2 x˙，因此整个机器人与接触面的碰撞模型可以表示为：F＝mx¨+Kp2 x+Kv2 x˙，其中x为脚掌与平面的接触位移，Kp2为弹簧刚度系数，Kv2为阻尼系数。

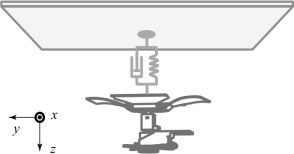
图8.5　仿壁虎机器人足端与接触平面的模型

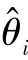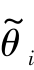在仿壁虎机器人上安装姿态传感器，将姿态传感器正放在机器人质心处。仿壁虎机器人的身体姿态随着其运动而发生改变，在第2章计算了机器人左前腿的运动学正／逆解以及足端位置与机器人重心及全局坐标系的关系，根据姿态传感器所测数据，修正足端位移量，再根据足端位移量求出机器人腿部各关节角度的变化量，以此调节机器人的姿态。仿壁虎机器人控制框图如图8.6所示。通过姿态传感器采集机器人姿态角变化，根据姿态角变化修正预设机器人足端运动轨迹，将修正后的预期轨迹与机器人实际运动轨迹作差，通过PD控制律来实现对机器人的运动控制。其中表示机器人空间运动轨迹期望值，表示修正后的运动轨迹期望值，Δ表示姿态角对运动轨迹的修正量，θi表示机器人实际运动轨迹，Δθi表示运动轨迹误差值，Fy表示机器人足端力，Δz表示机器人足端位移，α＾、β＾、γ＾表示机器人姿态角期望值，α、β、γ表示机器人姿态角实际值，Δα、Δβ、Δγ表示机器人姿态角误差值。

图8.6　仿壁虎机器人控制框图