通过对壁虎的运动观察，发现其在壁面运动过程中由四足相互协调，再根据黏／脱附需求配合肌腱的翻转实现在壁面的稳定爬行，尤其在负表面运动过程中，除了壁虎脚掌超强的黏附力以外，其足端脚趾之间以及四肢之间的锁合作用也很重要。本书所设计的仿壁虎机器人存在多层锁合结构，该结构为机器人实现负表面稳定黏附运动提供了保障。仿壁虎机器人多层锁合结构如图8.1所示。

图8.1　仿壁虎机器人多层锁合结构示意

步态是依靠腿部之间相互协调完成运动的规律。一个步态周期可分为支撑阶段和摆动阶段。单腿在支撑阶段所用时间占一个步态周期的比例为占空比，其中对角步态的占空比为0.5，三角步态的占空比约为0.75。仿壁虎机器人在负表面稳定黏附时，在不受外力的影响下可认为是静态的。以对角步态为例，对仿壁虎机器人进行静力学分析。

仿壁虎机器人的四条腿关于机器人质心对称，当机器人稳定黏附于光滑负表面时，处于对角线上的两条腿会内收形成“型”锁合结构，当其四只脚掌同时与负表面接触时，两对脚掌之间形成双“型”锁合结构。在不受其他外力情况下，认为仿壁虎机器人在负表面稳定黏附时处于静态，此时机器人受力示意如图8.2所示，其中与重力相反的方向为z轴正方向，水平向左方向为y轴正方向，根据右手法则得出垂直于yOz平面向内为x轴正方向。

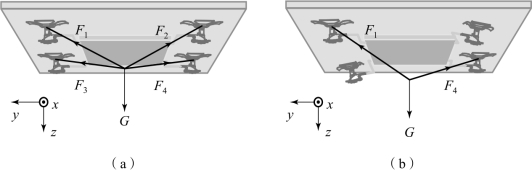
图8.2　仿壁虎机器人在负表面稳定黏附时的受力示意

（a）四只脚掌同时黏附；（b）两只脚掌黏附

由图8.2（a）可知，当仿壁虎机器人四只脚掌同时与光滑负表面接触黏附时，设机器人右前腿、右后腿、左前腿和左后腿受力分别为F1、F2、F3和F4，且这四个力在x轴、y轴和z轴上的分力分别为Fix、Fiy和Fiz，其中i＝1，2，3，4，分析仿壁虎机器人的受力情况可以得到如下方程：

由方程（8.1）可得，仿壁虎机器人四条腿之间的切向力互相抵消，其重力G与四个脚掌提供的法向黏附力之和相等。(www.daowen.com)

由图8.2（b）可知，当仿壁虎机器人只有对角的两只脚掌与光滑负表面接触黏附，另外两只脚掌悬空，且机器人处于稳定状态时，以图8.2（b）中的黏附状态为例，分析此时仿壁虎机器人的受力情况可以得到如下方程：

由方程（8.2）可得，仿壁虎机器人对角两腿之间的切向力互相抵消，其重力G与这两个脚掌提供的法向黏附力之和相等。

根据以上分析结果可得，为保证仿壁虎机器人在静止状态下实现负表面上的稳定黏附，机器人单个脚掌提供的最大法向黏附力至少大于等于自身重力的一半。因机器人结构对称，假设每个脚掌需要向仿壁虎机器人提供法向黏附力的大小为G／2。仿壁虎机器人的脚掌由四片对称的脚趾结构组成，当脚掌受到一定程度的外力时，对角的两片脚趾形成一个“型”锁合结构，四片脚趾之间形成双“型”锁合结构。当脚掌在负表面稳定黏附时，机器人在重力的作用下单个脚掌的受力示意如图8.3所示。

图8.3　仿壁虎机器人单脚掌在负表面稳定黏附时的受力示意

由图8.3可得，当仿壁虎机器人对角脚掌与光滑负表面接触黏附时，设其单只脚掌的各脚趾受力分别为f1、f2、f3和f4，且这四个力在x轴、y轴和z轴上的分力分别为fix、fiy和fiz，其中i＝1，2，3，4，分析机器人脚掌的受力情况可以得到如下方程：

由方程（8.3）可得，机器人脚掌的四片脚趾之间的切向力互相抵消，该脚掌提供的法向黏附力之和等于G／2。

综上所述，要实现仿壁虎机器人在光滑负表面的稳定黏附，机器人单脚掌提供的法向黏附力必须要不小于机器人自重的一半。考虑到仿壁虎机器人在光滑负表面的黏附运动过程中机器人落腿产生的碰撞、姿态调整、运动步态等因素的影响，仿壁虎机器人单个脚掌所能提供的最大法向力要远远大于机器人自身重力才能实现该机器人在光滑负表面上的稳定黏附运动。