电阻应变片式力传感器的标定是正常使用传感器前的重要工作，通过标定在力和电压信号之间建立对应关系。在标定时，加载已知砝码，测量桥路输出电压，建立力和电压之间的数学模型，这样当使用传感器时，通过测量的输出电压，即可得到传感器的受力方向和大小。由于该传感器的特殊结构，需要通过标定得到传感器的对称性、灵敏度、耦合性等参数。机器人足端三维力传感器的标定采用悬挂砝码的方式进行，图6.5（a）～图6.5（c）分别为对x、y和z轴方向标定示意图。

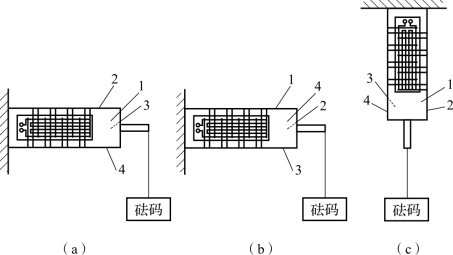
图6.5　传感器静态标定

（a）x轴方向标定示意；（b）y轴方向标定示意；（c）z轴方向标定示意
1，2，3，4—各个面上应变片

由于该传感器弹性体的结构和贴片方式，以及弹性体加工误差和应变片效果不同，传感器3个方向之间还存在一定的耦合性。因此，在使用该三维力传感器之前，需要通过传感器静态标定，计算传感器解耦矩阵，建立力向量F和桥路输出电压向量U之间的代数关系，消除维间耦合问题。

静态标定采用NI公司的SCXI系统信号调理设备（信号调理模块SCXI-1520和数据采集卡PCI-6052E），静态标定系统如图6.6所示。

图6.6　静态标定系统

静态标定时，将传感器4路桥路输出接至SCXI-1314接线端子。在Lab-VIEW中编写静态标定程序，程序结构和显示面板，将标定得到的数据保存为表单文件，利用Excel的线性拟合功能，通过最小二乘法拟合得到的数据，计算得到传感器输出曲线的斜率和线性度。

该三维传感器的理想情况是，x、y、z轴三个方向受力时，各方向的桥路输出之间互不影响，但实际上，力传感器各方向不是相互独立的，存在维间耦合，桥路电压信号变化量和传感器受力的关系应为

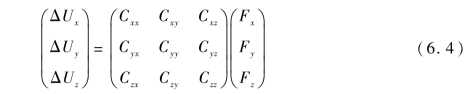
式中，ΔUx、ΔUy和ΔUz是由式（6.4）得到的三个方向的输出电压信号变化量；F为加载力向量；C为耦合矩阵。耦合矩阵通过标定数据计算得到，如Cxy的物理意义是在y轴方向上施加砝码时，x轴方向的电压信号变化量。因此，在标定时分别在x、y、z轴方向上加载定值砝码，每次加载时都测量传感器三个方向的输出电压变化量ΔUn，根据LabVIEW程序测量记录的输出电压变化量得到三组三维力信号特性曲线（x轴方向加载砝码时，三个方向的输出电压变化曲线；y轴方向加载砝码时，三个方向的输出电压变化曲线；z轴方向加载砝码时，三个方向的输出电压变化曲线），将得到的曲线进行最小二乘法线性拟合，得到拟合后的直线方程为y＝kx+b，k为耦合矩阵C中的元素。另外，由于单个方向的力是由两侧两个电桥信号之差测得，因此标定时还需要对传感器单个轴向的相反方向同时标定，检验其对称性。

在x轴正向和反向分别加载一组大小不等的砝码，在LabVIEW程序中测量电桥输出变化值，记录成表单文件，通过最小二乘法拟合成三条直线，即得到x轴方向输出信号特性曲线，三条直线方程中的斜率分别对应耦合矩阵中的Cxx、Cyx、Czx。x轴正向和反向输出特性曲线如图6.7所示。

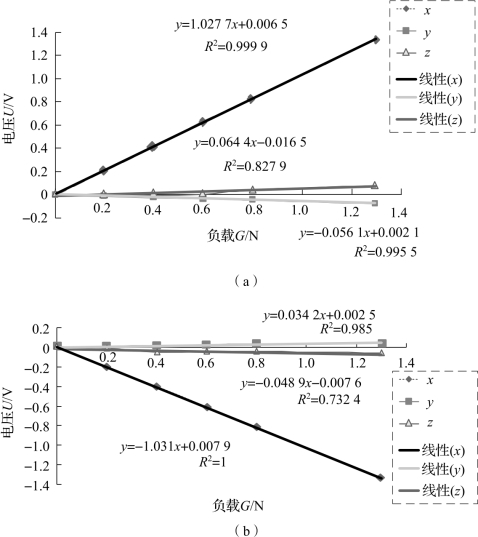
图6.7　x轴正向和反向输出特性曲线

由图6.7可知，传感器在x轴方向线性度高，各方向之间耦合小，x轴正负方向对称度高。斜率取多次正向负重测量中线性度最高的数据，得Cxx＝1.027 7，Cyx＝-0.056 1，Czx＝0.064 4。通过同样的方式，得到传感器在y轴方向和z轴方向的输出特性曲线图（图6.8、图6.9）。

由图6.8和图6.9可知，Cyy＝1.036 1，Cxy＝0.004 4，Czy＝-0.047 7，Cxz＝0.030 7，Cyz＝0.029 5，Czz＝0.189 3，即得到传感器耦合矩阵C：

(www.daowen.com)

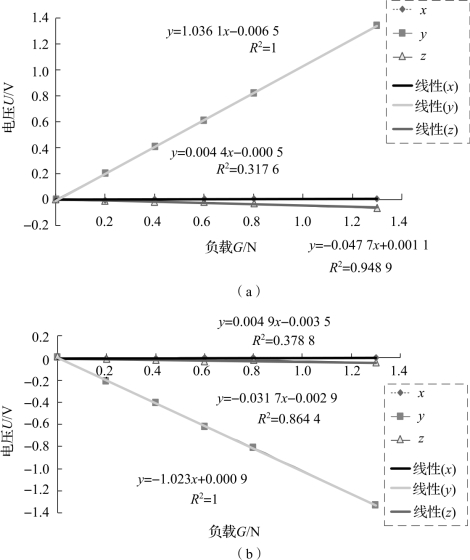
图6.8　y轴正向和反向输出特性曲线

式（6.4）可以写成：

由式（6.6）能将弹性体受到的力计算得到三维信号变化量。相反，通过测量传感器输出信号变化量计算传感器受到的足端力，将式（6.6）方程两边左乘C-1，可得

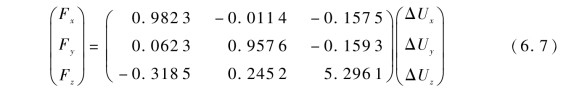
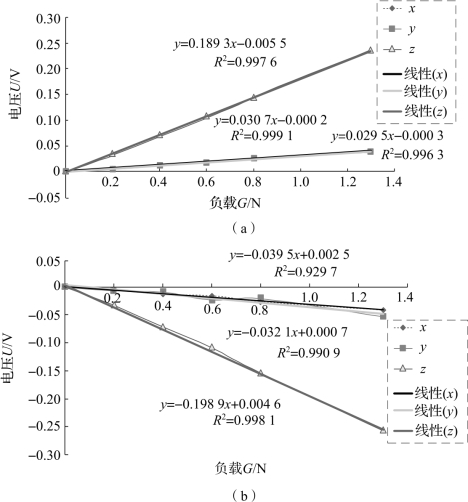
图6.9　z轴正向和反向输出特性曲线

将计算得到的解耦矩阵写入LabVIEW程序中，进行解耦验证。为验证力传感器对三维力的检测性能，在机器人足端安装该三维力传感器，并在垂直方向悬挂砝码，将机器人足端绕x、y、z轴旋转任意已知角度，即可知道该悬挂砝码对三维力传感器的x、y、z轴三个方向的已知作用力的理论值，与实际测量值相比较。该方法理论上可对传感器末端施加任意已知三维力。如表6.2所示，在传感器垂直方向悬挂100 g砝码，并绕x轴旋转75°，再绕z轴旋转45°，得到如表所示的x、y、z轴方向理论值。通过在LabVIEW程序中建立的解耦程序测量实际的三维力，得到的测量结果如表6.2所示，对x、y和z三维方向的力检测误差较小，满足实际小型机器人对足端三维力检测精度的要求。

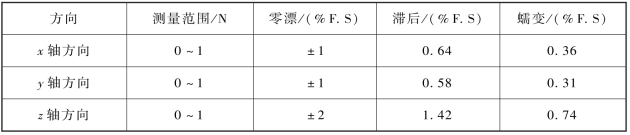
以此方法，分别对各个方向的力进行重复多次检测，整理相关数据，得到传感器标定结构，如表6.3所示。

表6.2　力传感器解耦实验表

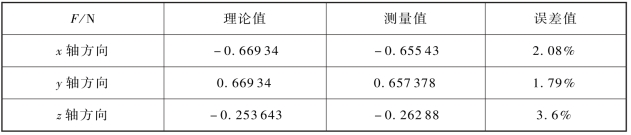
表6.3　传感器性能

实验结果表明：

（1）设计一种新型的电阻应变式三维力传感器，该传感器弹性体的特殊结构有效减小传感器的体积，结合4个1／4单臂电桥实现对三维力的检测。

（2）采用有限元仿真分析，初步判断复杂弹性体结构传感器的力学解耦性。

（3）利用NI的数据采集系统对三维力传感器进行静态标定，并计算三维力传感器解耦矩阵，三维力传感器测量误差较小，满足微小型机器人的工作需求。实验验证解耦矩阵的正确性，经解耦后的三维力传感器能准确测量出空间三维力。