使用步态规划程序可以规划出不同类型的步态，下面以对角和三角步态为例来进行程序的规划应用。

1.对角步态

规划的对角步态的参数设置分别为：前进时间＝6 s，前进距离＝92 mm，抬腿角度＝2°，抬腿时间＝0.5 s，前腿x轴方向位移＝54.8 mm，前腿y轴方向位移＝69 mm，前脚掌落地点偏移角＝90°，占空比＝0.5 s，后腿y轴方向位移＝23 mm，后脚掌落地点偏移角＝90°，左后腿偏移量＝0，左前腿偏移量＝0.5，右后腿偏移量＝0.5。其步态如图3.12所示。

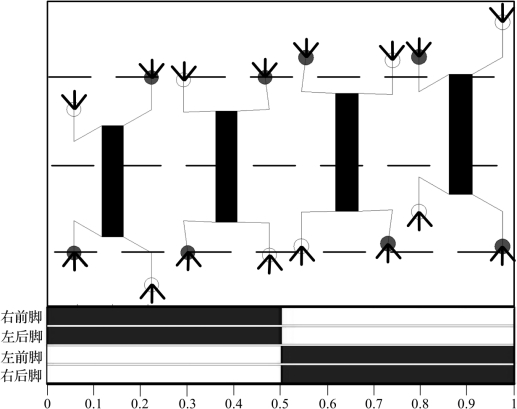
图3.12　对角步态

从图中可以看出规划的机器人运动时，身体始终呈直线，脚掌落地时的姿态始终与身体平行。

右前腿相应三个关节的转角随时间变化的曲线如图3.13所示。

从图中可以看到关节变化曲线平滑，无尖峰，有利于电动机驱动，驱动效率高，符合设计要求。

2.三角步态

所规划的三角步态，其中参数设置分别为：前进时间＝6 s，前进距离＝70 mm，抬腿角度＝2°，抬腿时间＝0.5 s，前腿x轴方向位移＝55 mm，前腿y轴方向位移＝65 mm，前脚掌落地点偏移角＝100°，占空比＝0.75 s，后腿y轴方向位移＝20 mm，后脚掌落地点偏移角＝100°，左后腿偏移量＝0.75，左前腿偏移量＝0.25，右后腿偏移量＝0.5。

从图3.14中可以看到与对角步态不同的是机器人在爬行过程中身体有左右摆动，整个运动过程模拟自然状态下壁虎的爬行姿态，并且可以看到脚掌姿态在整个运动过程中也在不断变化。

右前腿三个关节的转角随时间变化的曲线如图3.15所示。

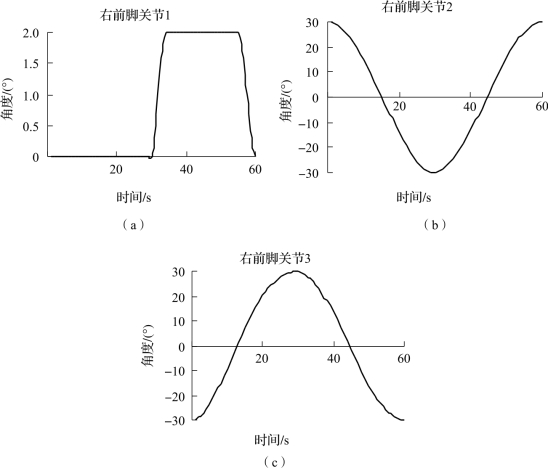
图3.13　对角步态下右前腿3个关节角度曲线

（a）对角步态下右前腿第1关节角度曲线；（b）对角步态下右前腿第2关节角度曲线；（c）对角步态下右前腿第3关节角度曲线(www.daowen.com)

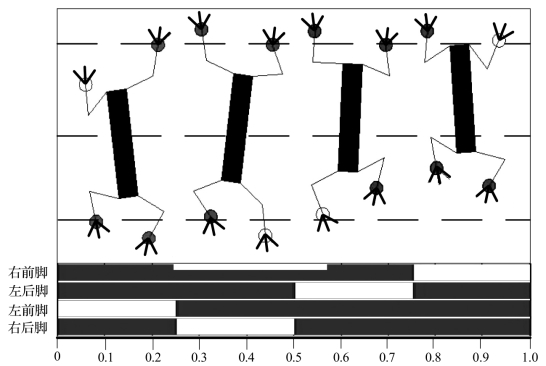
图3.14　三角步态

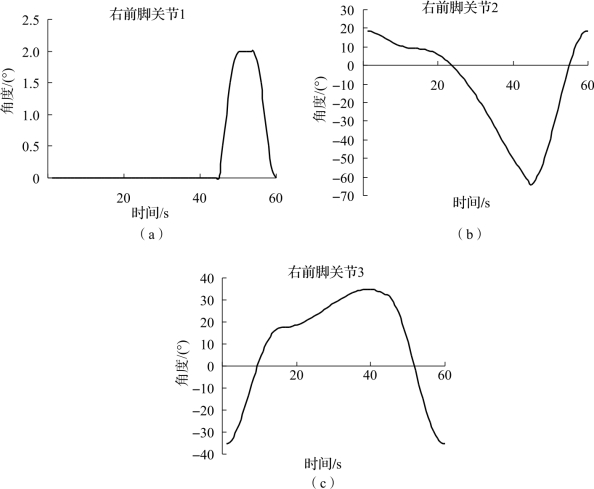
图3.15　三角步态下右前腿3个关节角度曲线

（a）三角步态下右前腿第1关节角度曲线；（b）三角步态下右前腿第2关节角度曲线；（c）三角步态下右前腿第3关节角度曲线

从图3.15可以看出，在规划的机器人运动过程中关节转角曲线平滑，有利于电动机驱动，驱动效率高，符合设计要求。

选用上面规划的对角步态数据，在ADAMS中建立运动学仿真环境，根据步态规划结果所提供的各关节转角数据，给各个运动副施加相关的运动约束，实现机器人的运动仿真，其仿真结果如图3.16所示。

图3.17（a）与图3.17（b）分别为机器人右前腿1关节即2号电动机转动角速度和角加速度曲线，可见角速度曲线过渡平滑，角加速度曲线在步态准备阶段有幅度较大的跳动，在步态周期内，最小值为-33.37°／s2，最大值为33.05°／s2，无过大的瞬时加速度，说明电动机不会因为较大冲击产生无法预期的振动。图3.18为右前腿2关节即3号电动机的输出转矩，可知最大转矩为100 N·mm，最小值为-91.43 N·mm，我们实际选用的HS-65MG型伺服电动机在6 V时，扭矩可达220 N·mm。所以根据上述分析，在本书设计的对角步态下电动机驱动平稳，驱动效率高，符合设计要求。

图3.16　对角步态仿真

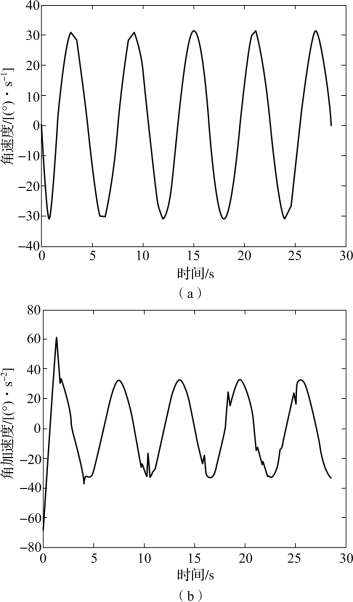
图3.17　右前腿1关节角速度和角加速度曲线

（a）右前腿1关节角速度曲线；（b）右前腿1关节角加速度曲线

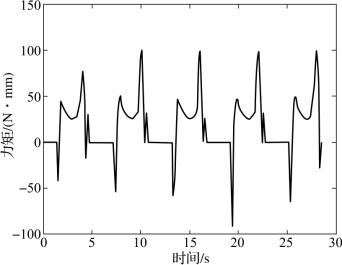
图3.18　右前腿2关节输出转矩