在本书的步态规划方法中身体运动由两部分合成：在前进方向的直线运动和绕身体中心点的转动。所以对于身体轨迹的规划，也相应包含两个方面：前进方向直线运动轨迹的规划和绕身体中心点运动轨迹的规划。以身体中心点为原点O，机器人前进方向为y轴方向，垂直于前进方向为x轴方向建立直角坐标系，如图3.3所示。

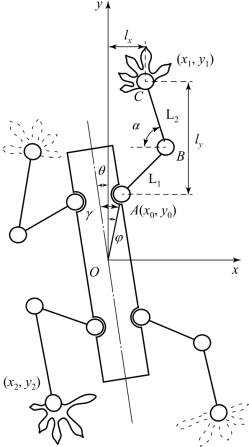
图3.3　机器人整体坐标

其中，连杆L1、连杆L2长度分别为l1、l2，OA的距离为l0，身体绕中心点O的转角为θ，杆OA与身体中心线夹角为γ，OA与y轴夹角为φ。

设前进周期时间为T、前进距离为D，利用余弦插补公式可得每一时刻身体在y方向上的位移：

式中，d1、d2分别是运动周期开始时和结束时身体中心点在y轴方向上的位移，tf为运动周期时间，S（t）为运动周期内t时刻身体中心点在y轴方向上的位移。

通过计算可以得到运动周期内身体中心点在y轴方向上的位移量S。

在壁虎运动过程中，前脚掌姿态与落点位置对整个运动过程的稳定性与协调性有重要的影响，同样在仿壁虎机器人的运动过程中，由于脚掌材料设计成仿壁虎微黏附阵列，具有各向异性的黏附特性，与壁虎脚掌类似，所以在进行仿壁虎机器人步态规划时考虑其前脚掌姿态和落点位置是非常必要的。(www.daowen.com)

在原有的步态规划方法中，机器人前脚掌落点位置不可选择，它只能随着步幅的变化做一定的调整，同时脚掌摆放方向始终平行于运动方向，机器人对前脚掌姿态和落点位置缺乏有效控制，这对于整体的运动规划是不利的。

本书提出的步态规划方法中，通过设定前脚掌相关的三个参数，即落点相对于腿根部在y轴方向上的相对位移ly、落点相对于身体中心点O在x轴方向上的相对位移lx和连杆L2与x轴方向的夹角α，如图3.3所示，来控制前脚掌姿态和落点位置。

首先计算A点的坐标（x0，y0）

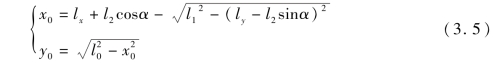
由此可算出φ＝arctan（x0／y0），令θ＝γ-φ，得出的β作为身体绕中心点O的最大转角（β＝θmax），两只前脚掌落点所设定的参数相同且脚掌结构对称，所以身体绕O点向左和向右的最大转角相同。

然后结合前进周期时间T利用余弦插补公式可插补出机器人身体在整个周期运动过程中绕身体中点O的转角变量Z：

式中，β1是右前脚掌落下时身体绕中心点的转角，β2是左前脚掌落下时身体绕中心点的转角，tf为运动周期时间，Z（t）为身体在周期内t时刻绕中心点的转角。