仿壁虎机器人逆运动学的分析过程与正运动学分析过程完全相反，且逆运动学分析的结果不唯一，但可以根据其他约束条件求得唯一解。本书采用代数反变换求解运动学逆解，求解过程如下：

首先将方程（2.14）等号左右两边同时左乘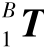-1，可得

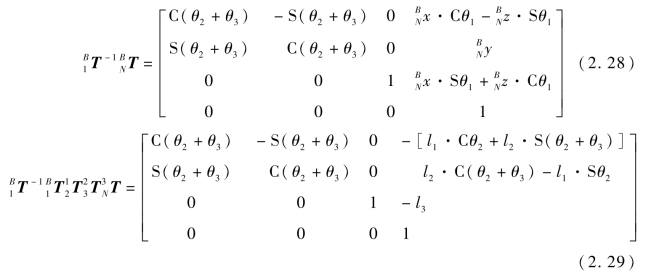
比较方程（2.28）与方程（2.29）的矩阵元素，可得

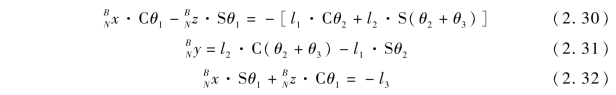
设

则有

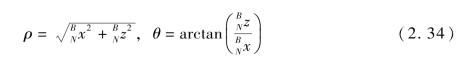
将方程（2.33）代入方程（2.32）可得

根据方程（2.35）可求得

将方程（2.34）代入方程（2.36）求得θ1为

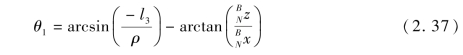
将方程（2.30）～方程（2.32）两端平方并求和，可得

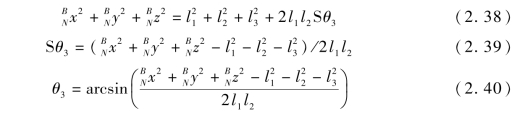
将方程（2.27）等号左右两边分别左乘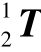-1，则

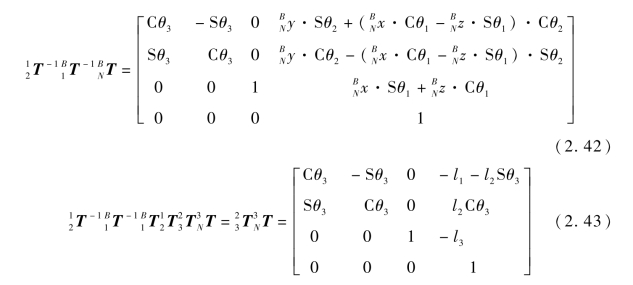
比较方程（2.42）与方程（2.43）的矩阵元素，可得

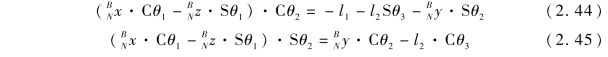
将方程（2.44）和方程（2.45）左右两边平方并相加，可得

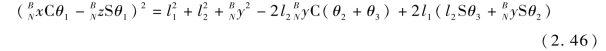
将方程（2.37）和方程（2.40）代入方程（2.46）计算可得(www.daowen.com)

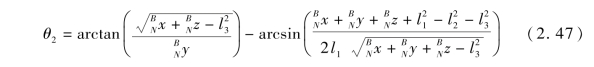
为验证计算所得仿壁虎机器人运动学逆解的正确性，在MATLAB／SimMechanics中对机器人的左前腿进行建模并仿真，其模型如图2.12所示。

设仿壁虎机器人杆件参数为l1＝50、l2＝70、l3＝60（单位为mm），则该机器人足端位置为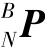＝［-50 70-60］T时对应的各关节转角为0°，给机器人足端一个y方向的正弦输入信号，机器人腿部在xOy平面内来回摆动，机器人左前腿足端轨迹位移曲线如图2.13所示，从图中可以看出仿真结果与预期一致，即该逆解计算正确。

假设仿壁虎机器人长为2a，宽为2b，选取机器人质心位置OG（OC）为原点建立全局坐标系ΣG（OG-xGyGzG），设机器人前进方向为x轴正方向，竖直向上方向为z轴正方向，根据右手螺旋定则确定的第三方向为y轴正方向。腿基坐标系、质心坐标系与全局坐标系的姿态变换示意图如图2.14所示。其中P1，P2，P3，P4分别表示左前、左后、右前、右后足端。

ΣC在全局坐标系ΣG中的位姿可用机器人上的姿态传感器测出，根据以上条件即可算出仿壁虎机器人左前腿足端在全局坐标系ΣG位姿的唯一表示。

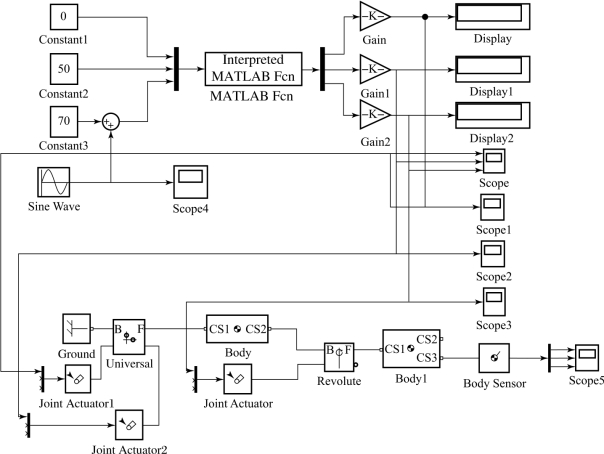
图2.12　运动学逆解验证模型

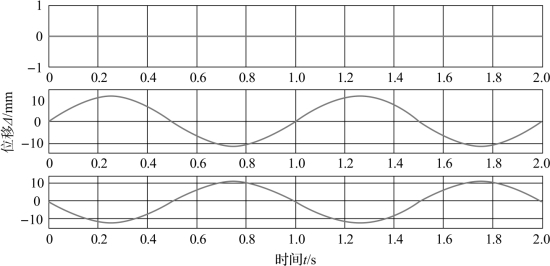
图2.13　机器人左前腿足端轨迹位移曲线

本书采用z-y-x转序的欧拉角来描述仿壁虎机器人在运动过程中姿态角的变化。假设四足机器人运动过程中的RPY（Roll、Pitch、Yaw）角分别为α、β、γ，则仿壁虎机器人的姿态变换矩阵为

计算式（2.48）可得仿壁虎机器人姿态旋转变换通式为

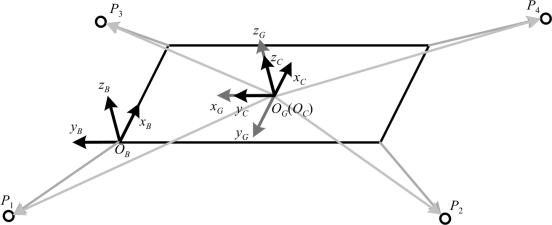
图2.14　姿态变换示意

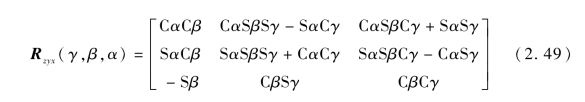
则仿壁虎机器人质心坐标系相对于全局坐标系的旋转矩阵可表示为

即仿壁虎机器人质心坐标系相对于全局坐标系的变换矩阵可表示为

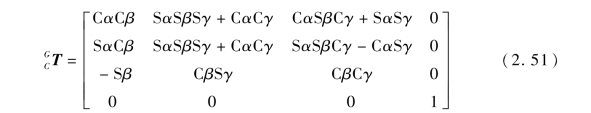
仿壁虎机器人基坐标系相对于质心坐标系的旋转矩阵为

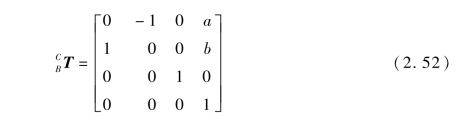
则仿壁虎机器人基坐标系原点在质心坐标系中的矢量表示为Q＝［a b 0 1］T。

假设仿壁虎机器人足端位置在全局坐标系中的矢量（步态规划时给出）表示为P＝［x y z 1］T，则可以求出仿壁虎机器人足端位置相对于其基坐标系的位置矢量为

仿壁虎机器人的关节坐标可根据本小节中所求逆解进行计算。