仿壁虎机器人在运动过程中，腿部摆动的位置和姿态都是相对于机身的运动，所以可将每条腿看作是基座位于机身上的拥有三个自由度的串联机械臂。由于仿壁虎机器人基坐标系ΣB与质心坐标系ΣC的位置关系是固定不变的，质心坐标系在全局坐标系中的变化可知，为简化计算，只计算关节变量相对基坐标系ΣB的关系，进而计算各关节坐标系相对ΣG（ΣG为以机器人质心OG为原点建立的全局坐标系OG-xGyGzG）的位姿。假设坐标系ΣB为基准坐标系，坐标系ΣN为足端坐标系，则仿壁虎机器人足端脚掌的位姿可通过坐标系ΣN相对于坐标系ΣB的位姿来表示。

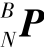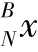
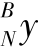
设机器人足端坐标系ΣN的原点在参考坐标系ΣB中的位置为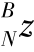＝［］T。设关节J1绕Y轴旋转的角度为θ1，其变换矩阵为T1；关节J2绕Z轴旋转的角度为θ2，其变换矩阵为T2；从坐标系Σ2平移到坐标系Σ3的平移矩阵为T3；关节J3绕Z轴旋转的角度为θ3，其变换矩阵为T4；从坐标系Σ3平移到足端坐标系ΣN的平移矩阵为T5。求得相邻坐标系之间的齐次变换如下：

式中，C代表cos（），S代表sin（），根据式（2.10）～式（2.13）求得足端对基坐标系ΣB的齐次变换矩阵如方程（2.14）所示：(www.daowen.com)

其中

方程表示仿壁虎机器人左前腿关节空间与运动空间的转换关系。当足端轨迹已知（即θ1，θ2，θ3已知）时，可求出足端相对于腿基坐标系ΣB的位姿，ΣB可由质心坐标系ΣC平移得到，即可算出仿壁虎机器人左前腿足端在全局坐标系ΣC位姿的唯一表示。为了验证运动学正解的正确性，以θ1＝0°，θ2＝-90°，θ3＝0°为例，根据式（2.24）～式（2.26）求得脚掌相对于ΣB的位置为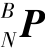＝［l2 l1-l3］T。仿壁虎机器人杆件参数为l1＝50、l2＝70、l3＝60（单位为mm），求得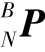＝［70 50-60］T，与计算结果一致。