在金属的实际切削过程中，刀具前刀面和切屑之间，刀具后刀面和工件之间发生着剧烈的摩擦，在实际的刀—屑接触界面存在两个区：黏结区和滑动区。这是由于法应力的分布不均匀，导致了靠近切削刃处较大，而远离切削刃处较小。在黏结区附近的单位切应力等于材料的剪切屈服强度，黏结区接触类型为紧密型接触，它的摩擦不服从古典摩擦法则。根据摩擦学的原理可知，在摩擦过程中的实际接触面积只占我们所看到的接触面积的很小一部分，在外加载荷的作用下，我们可以将摩擦表面间的接触状态看作由若干粗糙凸峰相互接触的组合，我们称之为峰点型接触，它的摩擦服从古典摩擦法则，各点的摩擦系数相等。摩擦接触模型如图2-1所示。

图2-1　摩擦接触模型示意图

一般条件下，金属切削时，黏结区的摩擦力要比滑动区摩擦力大很多，前刀面的摩擦主要是由紧密接触区的摩擦起主要作用。因此，从切削时刀—屑接触理论分析，在刀—屑接触区制备合理的表面织构能够改善刀—屑接触区的接触类型，同时结合固体润滑技术，能够改变刀—屑接触界面之间的摩擦接触状态，减小刀—屑接触摩擦系数进而减小摩擦力。

假设基体材料的极限剪切强度τs，根据强度理论的一般规律，摩擦副开始滑动的条件是：

σ2+ατ2s=σ2%b

（2-1）

式中：σ为法向载荷产生的压应力；σb为基体材料的抗压屈服极限；α为与基体材料性能有关的常数，且α＞1。其中：

式中：P为法向载荷；F为摩擦力；Ar为实际接触面积。

将式（2-2）和式（2-3）代入式（2-1）中可得：

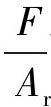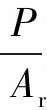由黏着摩擦理论可知，当摩擦力F不断增大时，由式（2-4）可知实际接触面积Ar亦随之增加，而σb和P保持不变，这样，相对于而言，的数值很小，则由式（2-1）和（2-4）得：

σ2b≈ατ2s

（2-5）

假设在法向载荷作用下的粗糙凸峰黏着点处，有一薄层润滑膜，其剪切强度极限为τf，假设τf=cτs，c是小于1的常数，由公式（2-1）可得有润滑膜的摩擦副开始滑动的条件为：

根据公式（2-5）求得：

σ2+ατ2f=σ2b

（2-6）

σ2b=ατ2s=ατ2f/c2

（2-7）

将公式（2-7）代入式（2-6），进而可求得表面有润滑膜的摩擦副摩擦系数为：

显然，如果c趋近于1，则μ趋向无穷大，这说明纯金属表面在真空中产生极高的摩擦系数。而当c值减小时，摩擦系数μ降低，可减小摩擦副间的摩擦。当c值很小时，摩擦系数μ可表示为：

式中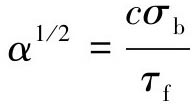：，代入公式（2-9），可得摩擦系数为：

由于τf为软表面膜的剪切强度极限，σb为硬基体材料的抗压屈服极限，故有：

具有软材料表面膜的摩擦副滑动时，黏着点的剪切发生在膜的内部，其剪切强度较低，因此，在载荷P一定的条件下，当基体材料相同，摩擦面之间存在剪切强度较低的润滑膜时，同样能够降低摩擦过程中的摩擦系数。

实际摩擦条件下材料一般处于边界润滑状态。边界润滑是指摩擦副界面上只存在一层极薄的润滑膜，这层极薄的润滑膜成为边界膜。由于边界膜太薄，不足以使摩擦副两表面分隔开。(www.daowen.com)

在边界润滑条件下，摩擦力F可看作是剪断表面黏着部分的剪切力F黏与剪断边界润滑膜的剪切力F膜之和，即：

F=F黏+F膜

其中：F黏=kArτs，F膜=（1-k）Arτf。

（2-12）

式中：k为接触面上发生固体接触部分Ar所占比例。

所以摩擦力F可表示为：

F=Arτc=Ar[kτs+（1-k）τf

（2-13）

式中：τc为摩擦表面的平均剪切强度。

下面分析边界润滑状态下的摩擦系数，由于表面膜很薄，且强度很低，实际载荷仍由基体承受，故边界润滑时σb基本保持不变，由此可得出边界润滑时的摩擦系数为：

当k=0时，即摩擦副处于边界润滑状态，由公式（2-14）可得摩擦系数为：

可见，边界润滑状态下的摩擦系数同样与润滑膜的剪切强度τf有关，当σb为一定值时，润滑膜的剪切强度τf越低，摩擦系数越小；另外，当表面平均剪切强度τc保持不变时，增加摩擦表面的平均压应力σb也可降低摩擦系数。

从原子层角度分析摩擦表面存在润滑膜的摩擦过程。根据G A汤姆林逊在1929年提出了材料的摩擦磨损原子模型。假设两个紧密接触的物体之间的原子界面如图2-2所示，材料的原子结构如图中“〇”所示，平面上两个方向的晶格常数都是a，而对摩材料的表面原子（和所研究材料相接触的那些原子）用正六边形表示，滑动摩擦前处于黑色图形的位置。向左滑动x距离后，分别到达虚线六边形的位置。

下面根据晶格内原子所受到力的性质，推导摩擦的表达式。

图2-2　摩擦表面的原子模型

假设固体中每个原子所受到的引力和斥力平衡。当两个物体接触的时候，接触表面原子的距离可以近到足以使对面原子进入斥力场中，即实现两个表面之间的原子结合。此时，分开这个表面所需的能量就是摩擦阻力。

因为工程表面的粗糙性，两个配合表面上只有很少原子（n0）进入作用区。考虑在两接触表面上施加载荷P以后，发生如图所示在记号x部位的原子一原子接触。现在假设此时有水平力F作用，使两个表面发生滑动，距离为X。相对运动过程中，原子键的结合和断裂次数为（n0X/a）。这里隐含运动过程中相互接触原子的对数n0保持不变的假设。显然这种假设有一定的问题，这里引入修正系数K。则原子和原子之间碰撞次数为：

等式的两端同时乘单个原子键的能量e，则：

也可以写作：

由以上分析可知，在其他条件不变的情况下，单个原子键的能量e就成为摩擦系数大小的关键。当摩擦表面有固体润滑膜的存在时，由于固体润滑膜的原子键的能量远小于基体，故摩擦系数降低。

切削过程中，切屑和前刀面之间的摩擦力（Ff）可由以下公式计算得来：

其中Ar为刀—屑实际接触面积，lf是刀—屑接触长度，Aw是切削宽度，τc是刀屑接触面润滑膜的剪切强度。

公式（2-19）表明摩擦力的大小直接与切削宽度Aw和刀屑接触面润滑膜的剪切强度τc有关。在之前的研究中，已经证实原位成型微织构自润滑陶瓷刀具微织构的存在将减小刀—屑接触长度。同时随着磨粒在流屑作用下挤入微沟槽，储存在微沟槽内的石墨润滑剂将溢出，并涂覆在前刀面上形成一层润滑膜，降低了刀屑接触面润滑膜的剪切强度τc，因此微织构的存在在一定程度上会提高切削性能。