1.有效数字及运算规则
(1)有效数字 在测定过程中实际能测到的数字称为有效数字。为了得到准确的分析结果,不仅要准确地测量,而且还要正确地记录和计数,即记录的数字不仅表示数量的大小,而且要正确地反映测量的精密程度。例如,用一般的分析天平称得某物体的质量为0.8390g,这一数值中,0.839g是准确的,最后一位数字“0”是可疑的,可能有上下一个单位的误差,即其实际质量是(0.839±0.0001)g范围内的某一数值。此时称得的绝对误差为±0.0001g,相对误差为
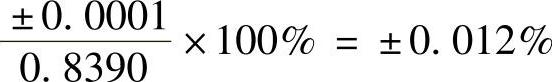
若将上述称量结果写成0.839g,则该物体的实际质量将为(0.839±0.001)g范围内的某一数值,即绝对误差为±0.001g,而相对误差为±0.12%。可见,记录时多写一位或少写一位“0”数字,从数字角度看关系不大,但是记录所反映的测量精确程度无形中被夸大或缩小了10倍。所以在数据中代表着一定的量的每一个数字都是重要的。
在计算测定结果时,首先应确定有效数字的位数。如在分析天平上称得某物的质量为0.0425g,此数据具有三位有效数字,数字前面的“0”只起定位作用,不是有效数字。又如某物质量为0.4300g,后面的两个“0”表示该物质量准确到小数点后第三位,第四位可能有±1的误差,所以这两个“0”是有效数字,数据0.4300具有四位有效数字。
(2)运算规则 在分析测定过程中,往往要经过几个不同的测量环节,例如用减量法称取试样过程中,要称取试样倒入前后称量瓶的质量,但这几个数据的准确度不一定完全相等。按照规定的计算规则,合理地取舍各数据的有效数字,既可节省时间,又可避免得出不合理的结论。一般根据下列规则进行运算。
几个数据相加或相减时,其和或差的有效数字的保留,应依小数点位数最少的数据为根据。例如:将0.0842、54.73及1.06872三数相加,由有效数字的含义可知,三个数中最末一位都是可疑的,其中54.73小数点后第二位已不准确了,即以小数点后第二位开始,即使与准确的有效数字相加,得出的数字也不会准确了,因此在运算之前,应以54.73为根据,将其他数字按四舍五入原则也取到小数点第二位,然后再相加:0.08+54.73+1.07=55.88。如不考虑各数据的准确度,一律相加得出55.88292则是不合理的。
乘除运算中取舍位数的原则与加减运算不同,加减运算有效数字的位数取决于绝对误差最大的那个数(上例中的54.73的绝对误差为±0.01,为三个数中最大者),乘除法中有效数字的位数取决于相对误差最大的那个数。例如下式:
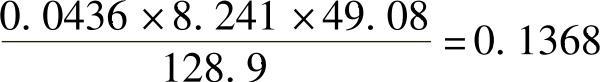
式中,各数的相对误差分别为:
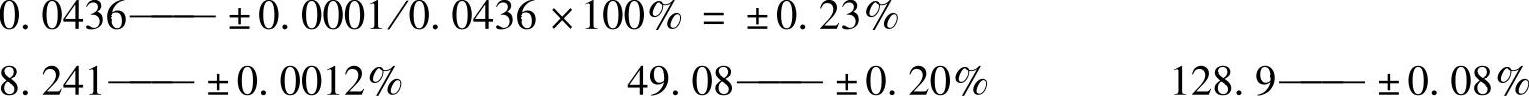
可见四个数中相对误差最大即准确度最差的是0.0436,是三位有效数字,因此计算结果也应取三位有效数字0.137。如果把计算得到的0.13681作为答数就不对了,因为0.1368的相对误差为±0.0073%,而在实际测量中没有达到如此高的准确程度。
在取舍有效数字位数时,还应注意下列几点:
1)在分析化学计算中,经常会遇到一些分数,如取某物质量的1/5,这里的5可视为足够有效,即不能根据它只有一位数而影响计算结果的有效数字的位数。又如从120mL混浊液中吸取15mL时,也不能根据15/120只有二位或三位数来确定分析结果的有效位数。
2)若某一数据的第一位有效数字大于或等于8,则有效数字的位数可多算一位,如9.64虽只有三位,但可看作四位有效数字。
3)在计算过程中,应暂时多留一位数字,得到最后结果时,再根据四舍五入原则弃去多余的数字。有时,也采用“四舍六入五留双”的原则处理尾数,即当尾数≤4时舍去,尾数≥6时进位,而当尾数恰为5时,应视保留下来的末位数是奇数还是偶数,是奇数时就将5进位,是偶数时,则将5舍弃。总之,使保留下来的末位数为偶数。根据此原则,如将7.435和7.425处理成三位数,则分别为7.44和7.42。
4)在大多数情况下,表示误差时,取一位有效数字即已足够,最多取两位。
如果使用电子计数器计算定量分析的结果,特别要注意最后结果中有效数字的位数,应根据前述规则决定取舍,不可全部照抄计算器上显示的数字。
2.数据处理
在分析工作中最后处理分析数据时,一般都需要在校正系统误差和剔除错误的测定结果后,计算出结果可能达到的准确范围,即应算出分析结果中包含的随机误差。首先要把数据加以整理,剔除由于明显、充分的原因而与其他测定结果相差甚远的那些数据,对于一些精密度似乎不甚高的可疑数据,则按照本节所述的方法决定取舍,然后计算数据的平均值和各数据对平均值的偏差与平均偏差,最后按照要求的置信度求出平均值的置信区间。现分述如下:
(1)平均偏差 有两种表示方法,即算术平均偏差和标准偏差。
1)算术平均偏差(d),即

式中 X——任何一次测定结果的数据;
X——n次测定结果的平均值。
2)标准偏差又称均方根偏差(σ),当测定次数n→∞时,有

式中 μ——无限多次测定的平均值,称为总体平均值。即

显然,在校正系统误差的情况下,μ即为真值。
在一般的分析工作中,只做有限次数的测定,根据概率可以推导出在有限测定次数时标准偏差的表达式,即
 (www.daowen.com)
(www.daowen.com)
(2)置信度与置信平均值的置信界限 根据统计理论,把分析结果在某一范围内出现的概率称为置信度(也称置信水平或概率水平)。而将真值落在一个指定的平均值的范围内,这个范围就称为置信界限。由统计学可以推导出有限次数的平均值 与总体平均值(真值)μ的关系:即
与总体平均值(真值)μ的关系:即

式中 S——标准偏差;
n——测定次数;
t——在选定的某一置信度下的概率系数。
t值可根据测定次数从表6-17中查得。由表6-17可知,t值随测定次数的增加而减小,也随置信度的提高而增大。
表6-17 对于不同测定次数及不同置信度的t值
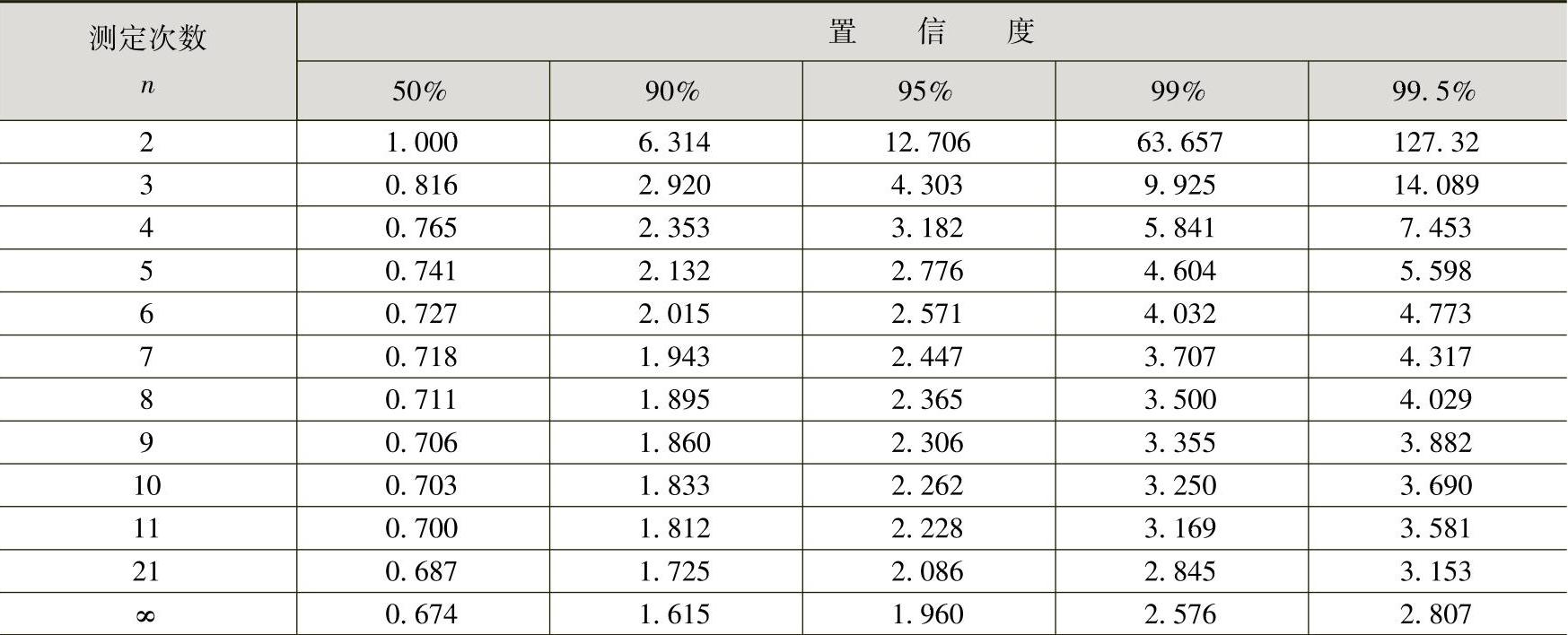
利用式(6-23)可以估算出,在选定的置信度下,总体平均值在以测定平均值为中心的多大范围内出现,即平均值的置信界限有多大。例如分析试样中某组分的含量,经过几次测定,在校正系统误差之后,由式(6-23)算出含量为47.15±0.23(置信度为95%),即说明该组分的几次测定的平均值为47.15,而且有95%的把握认为该组分的平均值的置信界限是在46.92到47.38之间。
(3)可疑数据的取舍 在实际工作中,常遇到一组平行测定中有个别数据的精密度似乎不甚高的情况。应注意,不可为了单纯追求实验结果的“一致性”,而把这些数据随便舍弃。下面介绍一种处理这类可疑数据的规则——Q检验法。
Q检验法:当测定次数n=3~10时,根据所要求的置信度(如取90%),按照下列步骤,检验可疑数据是否可以弃去。
1)将各数据按递增的顺序排列X1,X2,X3,…,Xn。
2)求出最大与最小数据之差Xn-X1。
3)求出可疑数据与其最邻近数据之间的差Xn-Xn-1或X2-X1。
4)按下式计算Q值
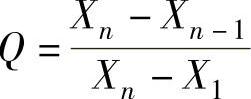 或
或 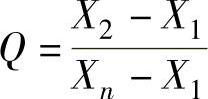
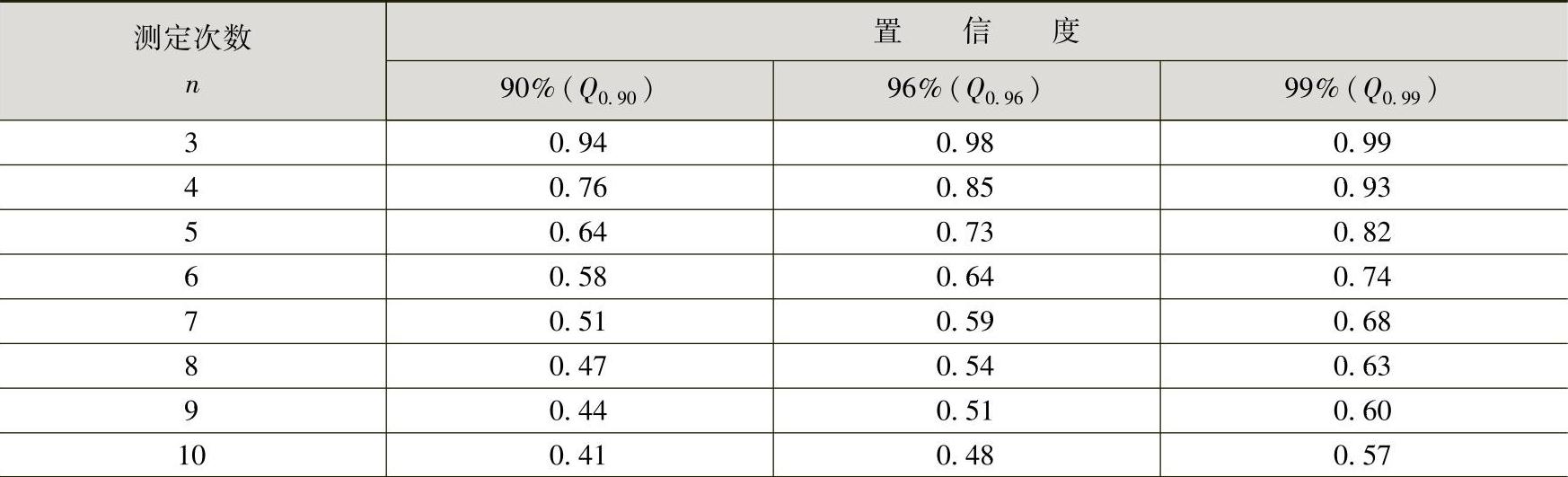
5)根据测定次数n和要求的置信度(如90%),查表6-18,得出Q0.90。
表6-18 不同置信度下,舍弃可疑数据的Q值表
6)将Q与Q0.90相比,若Q≥Q0.90,则弃去可疑值,否则应予保留。
例 在一组平行测定中,测得某物含量分别为22.38mg,22.39mg,22.36mg,22.40mg和22.44mg,试用Q检验法判断22.44mg能否弃去?(要求置信度为90%)
解 1)按递增顺序排列:
22.36,22.38,22.39,22.40,22.44
2)Xn-X1=22.44-22.36=0.08
3)Xn-Xn-1=22.44-22.40=0.04
4)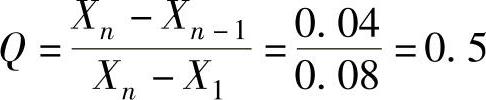
5)查表6-18,n=5时,Q0.90=0.64
Q<Q0.90,所以22.44mg应予保留。
如果测定次数比较少(如n=3),使用Q检验法时,Q恰好与表中查得Q值相等,按规定应弃去该可疑值,但是这样做较为勉强,如果可能的话,最好是再补测一、二次,而不是把剩下的两个数据取平均值记入检测报告。
若在三个以上的数据中,需要对一个以上的可疑数据用Q检验法决定取舍时,首先检验最小值,然后再检验最大值。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






