1.准确度

通常用误差表示分析结果的准确度。误差是指测定结果与真实值的差，差值越小，误差越小，即准确度越高。例如，称得某一物体的质量为7.7825g，而该物体的实际质量为7.7826g，测定结果与真实值的差为-0.0001g，得到的差值为绝对误差。若另有一物体的真实质量为0.7782g，测得结果为0.7781g，则测定的绝对误差为-0.0001g，两个物体的质量相差10倍，但测定的绝对误差都为-0.0001g，误差在测定结果中所占的比例未能反映出来，因此又引入了相对误差这个概念。

相对误差是误差在测定数值中的百分率，它等于绝对误差与所测定的真实值之比乘以100%。在上例中，相对误差分别等于

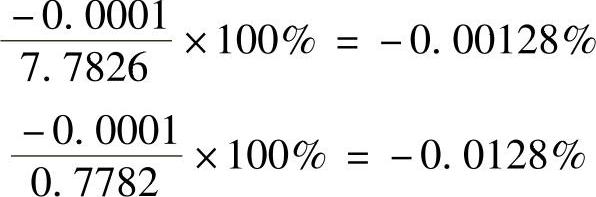
由于一般分析测定中误差的数值是相当小的，因此有时也用测定结果代替真实值，即相对误差近似地等于绝对误差与测定结果之比再乘以100%。

从相对误差的计算可以看出，在测定过程中测定的绝对误差虽然相同，但由于被测物的质量不同，相对误差也不同。显然，当被测定的量较大时，相对误差就比较小，测定的准确度就比较高。(www.daowen.com)

2.精密度

在实际分析工作中，往往要作几次平行测定，得到几个测定结果，它们之间相互接近的程度称为测定的精密度，常用偏差来表示。偏差是指个别测定结果与几次测定结果的平均值之间的差别。与误差相似，偏差也有绝对偏差和相对偏差之分。测定结果与平均值的差为绝对偏差，绝对偏差在平均值中所占的百分比为相对偏差。例如，测定某一样液的质量分别为6.5742g、6.5740g、6.5743g，可计算出测定的平均值为6.5742g，若其真值为6.5743g，则其误差与偏差见表6-16。

表6-16 误差与偏差