金属零件表面以及部件、装置和系统内腔的清洗过程是既有复杂的物理-化学过程，又有复杂的机械过程的综合过程。清洗效率取决于清洗剂的性质、污染物微粒的大小和性质、清洗工艺规范以及被清洗零部件及系统的结构特点。清洗后表面的污染度和残留污染物的种类基本上取决于清洗方法和清洗剂的种类。

现代机械的零件、部件及系统用于清洗的时间等于其制造和组装总时间的10%～15%。因此，在编制机械制造的工艺过程时，选择清洗剂、清洗方法以及确定清洗液的液动参数是非常重要的一步。金属表面粘附着的固态微粒、润滑油、油脂薄层等污染物，可通过机械作用、溶解、化学反应或洗涤等方法清除。在某些情况下，要采用综合性的清洗方法。

现在清洗机械零部件和系统时，广泛采用具有很强的物理-化学作用的清洗液。清洗液除了可以松散、破坏或溶解污染物层外，在一定条件下，还可以对固态污染物微粒施加机械作用。

因为金属表面上的污染物一般来说是固态微粒，腐蚀和氧化产物，润滑油、油脂等的聚合残渣的混合物。要清除它们往往要费很大气力，需要采用专门手段来完成该项工作。为了方便地清洗掉毛坯和零件表面聚合层中的固态污染物微粒，建议用化学活性强的清洗液冲洗。大多数情况下，清洗工作需在零件制造完毕后立即进行。

依据对清洗液与污染物微粒相互间液体动力作用的分析并参照试验研究结果，确定用清洗液流清洗零件金属表面的工艺规范（最佳工艺）。这里分析一下清洗液流清除污染物的机理。许多研究人员，虽然并不轻视清洗剂的活性所形成的那些物理-化学因素的意义，但倾向于认为清洗液对污染物的机械作用是决定清洗效率的基本条件之一。

用液流清洗金属表面的过程可以划分为下列几个相互间有关联的基本过程：污染物微粒剥离被清洗表面，液流使污染物处于悬浮状态，将污液送往过滤（净化）装置。

污染物微粒的剥离过程是整个清洗过程的基本组成部分。同时，从被清洗表面上剥离下来的污染物微粒应迅速地清除走，为此，清洗液应具有必要的悬浮和输送能力。

液体介质的悬浮能力是指液体能使一定粒度的固态微粒保持于悬浮状态的能力。根据液力输送理论，悬浮介质的悬浮能力取决于其组成及强度。悬浮能力还取决于悬浮物的性质和它的浓度。分散介质的悬浮能力通常以该介质能稳定保持处于悬浮状态的固态微粒的最大（临界）粒度及其数量来表示。现在大家公认：只有液体在湍流状态下才能可靠地输送悬浮状态的重微粒。

下面分析一下液流剥离、悬浮和输送污染物微粒的整个过程。作用于清洗表面污染物微粒上的力有：液体中污染物微粒的重力G，微粒附着于表面上的附着力F_ag，升力W_y（作用于微粒上的液动力主矢量的垂直分力），正向阻力W_x（作用于微粒上的液动力主矢量的水平分力，其作用方向与液流速度矢量的方向相同），如图4-5所示。因为需要清除的污染物微粒的实际粒度为0.5～100μm，而清洗时相当多的污染物微粒又是隐藏在液体边界层内的（所谓边界层是受粘滞力的作用，阻滞于表面附近的液层）。边界层阻碍了污染物微粒与相邻急剧运动的液层接触，这就使得附着的污染物微粒难以从清洗表面清除掉。

附着于清洗表面或突出于清洗表面周围的污染物微粒总体之上的单个污染物微粒承受着清洗液流的动力作用，而该动力作用是由微粒的正向阻力W_x引起的。在正向阻力W_x作用下，微粒相对于接触面移动（剪移）。由于微粒形状不同，正向阻力W_x迫使微粒在表面上滚动或滑动。微粒形状越接近于球形，微粒的移动越可能为滚动，而扁的和长的微粒则在表面上或靠近表面滑动。

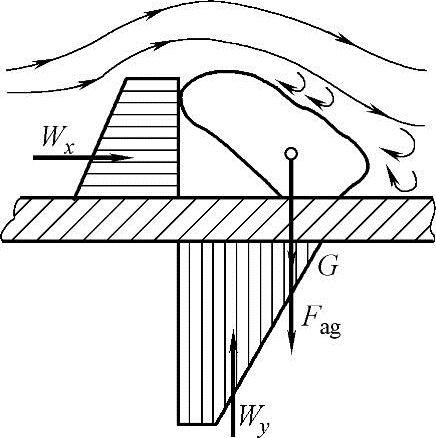
图4-5 作用在液流中被清洗表面上污染物微粒的力的示意图

很明显，如果在液流方向上作用于微粒的流体动力之和超过微粒与表面之间的摩擦力，微粒就可能从表面剥离下来。这个条件可用不等式表示为

W_x>f（G-W_y+F_ag）（4-3）

式中 f——微粒与表面间的摩擦因数。

微粒与表面之间的摩擦力取决于微粒与表面的结合力，而结合力则主要取决于微粒的重力G和附着力F_ag。

只要知道微粒的大小及其材质，微粒的重力很容易算出。粒度小于100μm，且表面积总和又很大的固态微粒相互间很容易牢固地结合在一起，并牢固地贴附于微粒沉积的表面上。这样的微粒，其表面也很容易吸附油性物质，使得微粒与清洗表面的结合力增强。

附着力取决于相互接触物体的性质、分子间作用力和电场作用力、毛细作用以及其他因素。微粒的附着力随粒度减小而增大。接触面浸油和湿润也导致附着力的增强。至今还没有通过理论和试验研究解决计算燃油、润滑油和液压系统用液中污染物微粒的附着力的办法。水中玻璃球贴附于钢制零件表面上的附着力，其计算式为

F_ag=kd_w（4-4）

式中 k——与附着的玻璃球数量有关的经验系数，单位为10^-5N/μm；

d_w——玻璃球的直径，单位为μm。

对于很小的污染物微粒，附着力可能比重力大n个数量级，因此附着力是使微粒贴附在被清洗表面上的基本作用力。

升力W_y促使污染物微粒剥离，而升力的产生是由于微粒周围有非对称的绕流。微粒下方有不流动的液体或是缓慢渗透着的液体，而微粒上方则有急剧流动着的液体。在具有这种非对称绕流的情况下，微粒下方的液体压力将超过微粒上方的液体压力。

根据H.E.茹科夫斯基的公式，球形微粒的正向阻力（N）为(www.daowen.com)

W_x=0.2πd²_uρv²（4-5）

式中 d_u——微粒直径，单位为m；

ρ——液体的密度，单位为kg/m³；

v——液体相对于微粒的速度，单位为m/s。

式（4-5）适用于球形微粒的阻力系数c_x=0.4用湍流（Re=2×10³～2×10⁴）清洗时的情况。从式（4-5）还可以看出，为了使微粒剥离，具有决定性意义的是液流的速度。如果微粒很小，或者微粒突出于沉积在表面上的其他微粒总体之外的部分不大，正向阻力，也就是作用于微粒上的拖曳力与液流速度的一次幂成正比。如果微粒较大，并大大突出于液体边界层之外，则正向阻力可取为与液流速度的平方成正比。通常以微粒中部截面重心处水平方向上的液流局部速度值作为计算液流速度。

在某一液流速度下，可看到最初一些微粒被推起，开始移动，其运动的稳定性也可能遭到破坏，结果微粒发生振动，离开清洗表面并在离表面不远处呈跳跃式移动。在一定条件下，剥离下来的微粒可能又重新沉积在表面上，也可能悬浮在液流中。

所谓剥离速度是指液流的某一平均速度，相当于发生微粒剥离时，微粒所在区域内的液流局部速度。微粒剥离过程的计算可归结为根据微粒的粒度对微粒剥离速度的计算。

由于微粒周围的绕流运动千差万别，而且微粒的粒度大小也不一样，不可能找出计算微粒剥离速度的通用公式来。为此，建议按微粒直径d_u与边界层厚度δ之比值，分别研究以下几种情况：当d_u<δ/3时，微粒隐于边界层流之内，微粒周围的绕流运动工况是平稳的层流；当d_u>5δ时，微粒突出于边界层之外，此时，微粒处于急剧运动的液流层的作用之中，因此，液流绕微粒流动时形成涡旋和发生涡旋中断的现象。中间过渡工况的特点是液流呈层流状，但也出现液流中断现象，从而形成涡旋。

对于粒度大于边界层厚度δ的某些微粒，微粒剥离瞬时的液流速度可按埃里定理计算，即

式中 v₀——微粒剥离瞬时的液体速度，单位为m/s；

ψ——总阻力系数，总阻力包括液体绕流流过微粒时微粒与清洗表面之间的摩擦阻力；

ρ_u，ρ——微粒及液体的密度，单位为kg/m³；

d_u——微粒直径，单位为m。

粒度为0.25～1.5mm的微粒，其剥离速度可以按流动光滑河床计算公式计算，即

式中 R——河床水力半径；

Re——液流的雷诺数。

处于中间区域的微粒的剥离速度为

微粒剥离所需的液流平均速度是随着微粒粒度的减小而升高的。这是由于边界层处的液体流动速度是很低的，因而作用于边界层内小微粒上的动力作用也非常小。为剥离微粒而需增高液体的局部速度决定了平均速度也要随之增高。小微粒剥离困难还由于它的附着力极大，因而也要求提高液流的平均速度。微粒的附着力取决于微粒的形状，微粒形状接近于球形或正多面体者，其附着力为最小，而扁平微粒由于与表面接触面积较大，其附着力也更高。微粒表面微观粗糙度越大，附着力越大。

研究表明，即使在清洗液具有中等平均速度的情况下，只要人为地使清洗液流的压力或速度波动，从而使液流产生扰动，也能有效地清除粒度为2～100μm的弥散分布的粉末状的污染物微粒。在清洗时创造条件，促使将污染物微粒粘附在被清洗表面上的结合迅速地被破坏，便可在一定程度上补偿清洗液流速不高的缺点。