求解线性代数方程组的数值计算方法很多，如高斯消元法、LU 分解法、迭代法等。算法选择要考虑算法的精度、稳定性、计算时间、内存占用量等因素。高斯消去法是常用的算法。

设n 维线性代数方程组为

求解这样的方程组最容易想到的方法是克莱姆法则求解，但应用该方法要计算（n＋1）个n阶行列式，计算量大得惊人，如果用计算机计算也要消耗内存和时间。高斯消元法能够实现人工计算的简单化，当然计算机的计算量也大大降低，可以节省内存和计算时间。

1.高斯消元法的原理

高斯消元法利用矩阵初等变换，将式（10-36）的系数矩阵A 变换为下三角内元素全为零，主对角线元素全为1的矩阵，然后逐个计算xi。

首先，形成式（10-36）的增广矩阵，即

然后，对A 进行n 次初等变换，即由，得

该过程的第k 次变换，又分为归一计算和消元计算两步。归一计算的目标是将第k 行主对角线元素变为1，消元计算的目标是将第k 列主对角线元素以下的所有元素变为0。计算公式为

最后，分n 次逐个计算变量，称为回代过程。计算公式为

【例10-11】　用高斯消元法求解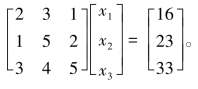

解：增广矩阵为

①第1 次消去：

归一计算：第1 行各元素除以a11，得

消元计算：将下三角的第1 列元素变为0，得

②第2 次消去：

归一计算：第2 行各元素除以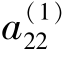，得

消元计算：将下三角的第2 列元素变为0，得

③第3 次消去

归一计算：第3 行各元素除以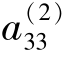，得

第1 次回代，从第3 行得(www.daowen.com)

第2 次回代，从第2 行得

第3 次回代，从第1 行得

2.主元高斯消元法

在高斯消元法的归一计算中，总是以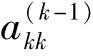为分母，当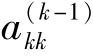的绝对值太小时，会产生很大的舍入误差，导致结果不可靠。选用绝对值最大的元素（称为主元）作为归一计算时的分母来克服此问题，称为主元高斯消元法。主元有列主元和全主元之分，列主元消元法是在本列剩余元素中选择主元，全主元消元法是在剩余的系数矩阵中选择主元。

【例10-12】　用列主元高斯消元法求解例10-11 中的线性代数方程组。

解：增广矩阵为

①第1 次消去

由于第1 列最大的元素a31＝3 是主元，因此将第1 行和第3 行对调，得

归一化计算：

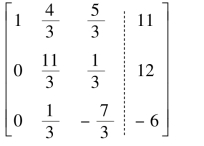
消元计算：＝

②第2 次消去

第2 列最大元素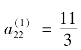是主元，不用对调。

归一化计算：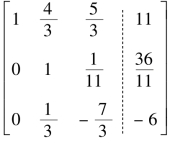

消元计算：＝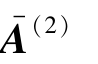

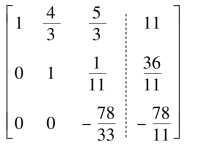
归一化计算：＝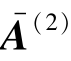

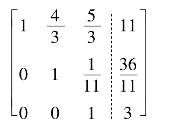
第1 次回代，从第3 行得

第2 次回代，从第2 行得

第3 次回代，从第1 行得