1.状态变量的选取
一个电路网络在任意时刻t0的状态是一组最少信息的集合,如x(t0)={x1(t0),x2(t0),…,xn(t0)},若t ≥t0加到电路网络的激励已知,则对于确定电路网络t≥t0的任何响应,x(t0)是一组必要且充分的信息。对于这组信息的变量x1(t0),x2(t0),…,xn(t0)称为电路网络的状态变量,是一组线性无关的变量。
当分析线性时不变动态电路时,必须预先确定电容的初始电压和电感的初始电流,结合电路在t>0 后的激励,就可以确定t >0 后的响应。因此,在线性时不变动态电路中,独立的电容电压与独立的电感电流一起构成电路的状态变量;而在非线性或时变电路中,独立的电容电荷与独立的电感磁链构成网络的状态变量。将状态变量写成形如x(t)=[x1(t)x2(t)… xn(t)]T的列向量,称为状态向量。
2.状态方程的建立
RLC 串联电路如图10-18 所示。
以RLC 串联电路的时域分析为例,列出以电容电压为求解对象的微分方程,即

这是一个二阶线性微分方程。用来确定积分常数的初始条件应是电容上的电压和电感中的电流在t=t0时的初始值。这里以t0时刻作为动态过程的起始时刻。
如果以电容电压uC和电感电流iL作为变量,电路方程有

将这两个方程略作改变,可得

这是一个以uC、iL为状态变量的一阶微分方程组,仍然是用电容上的电压和电感中的电流在t=t0时的初始值来确定积分常数。因此,该方程组就是描述动态电路的状态方程。
如果用矩阵形式列写上述方程组,则有

若令![]() ,则上述矩阵方程可变为
,则上述矩阵方程可变为

式中,A、B 分别为
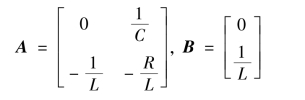
如果定![]() ,则状态方程还可以简写为
,则状态方程还可以简写为
![]()
式(10-32)为状态方程的标准形式。x 状态向量,v 输入向量。一般情况下,设电路具有n 个状态变量,m 个独立电源,则由n 个状态变量组成n 维列向量x,由m 个输入函数组成m 维列向量v,系数矩阵A 为n×n 阶方阵,B 为n×m 阶矩阵。
对于给定的电路网络,可直接列写状态方程。设网络是常态的,即其中不含纯电容回路和纯电感割集,可选电感电流和电容电压作为状态变量。列写状态方程的方法有多种,如等效电源法、观察法、拓扑图法。等效电源法和观察法介绍如下。
等效电源法:将电感电流iL等效为电流源,将电容电压uC等效为电压源,原电路网络等效为电阻网络,利用解电阻网络的各种方法求得电感电压uL和电容电流iC,它们是iL、uC和外施独立电源的函数,于是得到 的相关表达式,就得到状态方程。
的相关表达式,就得到状态方程。
【例10-6】 电路如图10-19(a)所示,试列写状态方程。
解:选uC、iL1、iL2为状态变量,列写状态方程为

图中电容、电感电流和电压的参考方向一致,其电压和电路的关系有(https://www.daowen.com)
![]()
先写出以下矩阵方程

式中,Al、Bl为常数矩阵。
将图10-19(a)中的电容用电压源等效替换,电感用电流源等效替换,得到图10-19(b)。认为电压源uC、电流源iL1、iL2为已知,整个电路为电阻电路。根据KCL 有
![]()
根据KVL,选取图(b)所示回路1、2,有
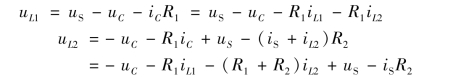
于是矩阵方程(10-34)可写为

进一步写出状态方程(10-33)的形式,即
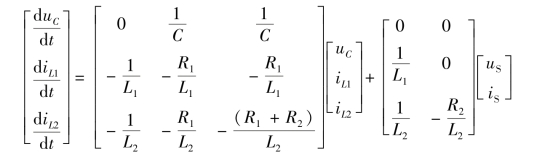
写成标准形式为
![]()
式中,x1=uC,x2=iL1,x3=iL2,![]() ,x=[x1x2x3]T,v=[uSiS]T。
,x=[x1x2x3]T,v=[uSiS]T。
观察法:借助于“常态树”,这种树的树支包含了电路中所有电压源支路和电容支路,它的连支包含了电路中所有电流源支路和电感支路。当电路中不存在仅由电容和电压源支路构成的回路和仅由电流源和电感支路构成的割集时,特有树总是存在的。可以任选一个“常态树”,对单电容树支割集列写KCL 方程,对单电感连支回路列写KVL 方程,消去非状态变量,再整理成矩阵方程形式。
【例10-7】 电路如图10-20(a)所示,试选一棵“常态树”,列写其状态方程。
解:选“常态树”如图10-20(b)所示。写图示割集的KCL 方程和回路的KVL 方程,有
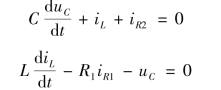
上述两式中iR1和iR2是非状态变量,需要消去,因此写iR1单树支割集的KCL 方程和iR2单连支回路的KVL 方程为
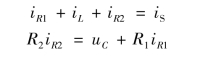
联立两式解出
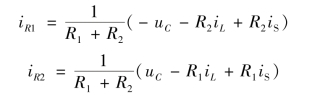
因此可得到状态方程为

写出矩阵形式为
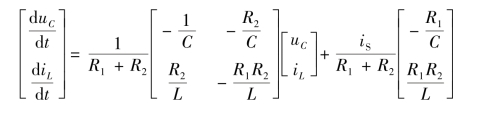
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





