结点电压法以结点电压为电路的独立变量，并用KCL 列出足够的独立方程。由于描述支路与结点关联性质的是矩阵A，因此用以A 表示的KCL 和KVL 推导结点电压方程的矩阵形式。矩阵A 表示的KVL 矩阵形式为

式中，un为结点电压列向量，u 为支路电压列向量。

矩阵A 表示的KCL 矩阵形式，即

式中，i 为支路电流列向量。式（10-26）和式（10-27）是导出结点电压方程矩阵形式的两个基本关系式。

对于结点电压法与回路电流法相同，也需要定义一个复合支路，列出该复合支路的伏安关系方程。复合支路如图10-15 所示，所有电压、电流的参考方向如图标注。

下面分3 种情况推导整个电流的支路电压方程的矩阵形式。

（1）当电路中无受控源，电感间无耦合时，第k

条支路的伏安特性有

对于整个电路有

式中，Y 称为支路导纳矩阵，它是一个对角矩阵。

（2）当电路中无受控源，但电感之间有耦合时，式（10-28）还要考虑互感电压的影响。当电感之间有耦合时，电路的支路阻抗矩阵Z 不再是对角矩阵，其主对角线元素为各支路阻抗，非对角元素是相应支路之间的互感阻抗。令Y＝Z－1，由可得

或者

这个方程形式上与式（10-29）相同，但其中的Y 由于互感导纳的存在而不再是对角矩阵。

（3）当电路中含有受控电流源时，设第k 支路中有受控电流源，并受第j 支路中无源元件上电压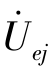或电流控制，且有。此时第k 条支路有

在VCCS 情况下，，而在电流控制电流源的情况下，。于是有

式中，当为电压控制电流源的电流时，Ykj＝－gkj；为电流控制电流源的电流时，Ykj＝βkjYj。

矩阵方程可简写为

这个方程形式仍然与情况1 相同。只是矩阵Y的内容不同。

下面推导结点电压方程的矩阵形式，重写所需3 组方程式，即

KCL

KVL

支路方程

将支路方程代入KCL 方程可得

展开上式有

(www.daowen.com)

再将KVL 方程代入上式有

或写为

式中，Yn≜AYAT为结点导纳矩阵，是一个（n－1）阶方阵，为独立电源引起的流入结点的电流列向量。

式（10-30）即为结点电压方程的矩阵形式。从式（10-30）中解出结点电压列向量后，由式（10-26）和式（10-29）可得到支路电压和支路电流列向量，即

【例10-4】　电路如图10-16 所示，图中元件下标表示支路编号。在下述两种情况下列出电路结点电压方程的矩阵形式，求：

(1)M12＝0；

(2)M12≠0。

解：图10-16（a）所示电路的有向图如图10-16（b）所示。如果选结点④为参考结点，则结点①、②、③的结点电压相量为，则关联矩阵A 为

电压源电压列向量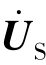＝0，电流源电流列向量为

结点电压列向量为

（1）M12＝0 时的支路导纳矩阵为

结点电压方程的矩阵形式为

代入各矩阵得

（2）M12≠0 时的支路导纳矩阵为

式中，Δ＝jω（L1L2－。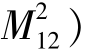

结点电压方程的矩阵形式为

将各矩阵代入得

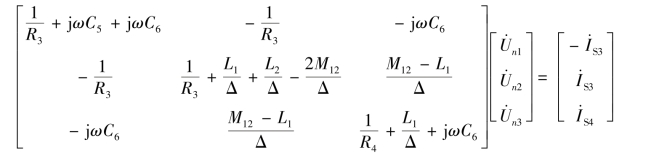
【例10-5】　电路如图10-17 所示，图中元件的下标代表支路编号，设，，请写出支路方程的矩阵形式。

解：图10-17（a）所示电路的有向图如图10-17（b）所示。如果选结点④为参考结点，支路导纳矩阵可写为

电流源向量与电压源向量为

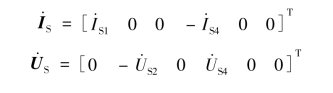
支路电路矩阵方程为

将导纳矩阵、电压源和电流源矩阵代入上式得