网孔电流法和回路电流法是分别以网孔电流和回路电流作为独立变量,应用KVL 列出所需的独立方程组进行电路分析的一种方法。由于回路矩阵B 充分描述了支路和回路的关联性质,因此可以用矩阵B 表示的KCL 和KVL 推导回路电流方程的矩阵形式,设回路电流列向量为i1,支路电流列向量为i,支路电压列向量为u,有

此外,还必须有一组支路的伏安特性方程,因此需要规定一条支路的结构和内容。在直流电路、正弦稳态电路分析或应用拉氏变换分析中,尤其是编写矩阵形式的电路方程时,一种有效的方法是定义一条“复合支路”。一条复合支路一般包含几种元件并按规定方式相互连接,回路电流法采用如图10-13 所示的复合支路,其中下标k 表示第k 条支路,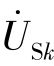 和
和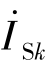 分别表示独立电压源电压相量和独立电流源电流相量,
分别表示独立电压源电压相量和独立电流源电流相量,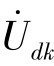 表示受控电压源的电压相量,Zk(或Yk)表示阻抗(或导纳),且规定它只可能是单一的电阻、电感或电容,而不能是它们的组合,即
表示受控电压源的电压相量,Zk(或Yk)表示阻抗(或导纳),且规定它只可能是单一的电阻、电感或电容,而不能是它们的组合,即
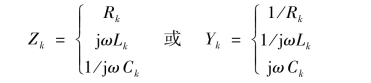
复合支路的定义规定了一条支路最多可以包含的不同元件数及其连接方式,但不是说每条支路都必须包含这几种元件,可以允许一条支路缺少其中某些元件,但对于回路电流法,不允许存在无伴电流源支路。图10-13的复合支路采用的是相量法,可以采用相应的运算形式,电压和电流的参考方向标注在图中,其伏安关系的相量形式为
![]()
下面分不同情况讨论。
(1)电路中没有受控源、电感之间无磁耦合的情况,对于第k 条支路,令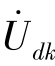 =0式(10-21)变为
=0式(10-21)变为
![]()
若设
支路电流列向量为
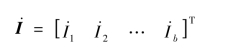
支路电压列向量为
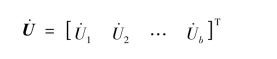
支路电流源的列向量为
![]()
支路电压源的电压列向量为
![]()
则整个电路有
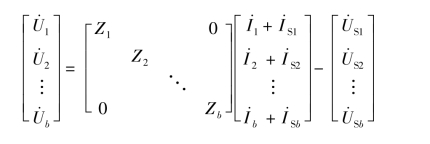
即
![]()
式(10-23)中Z 称为支路阻抗矩阵,它是一个对角矩阵。
(2)当电路中电感之间有耦合时,复合支路的伏安关系要考虑互感电压的作用。若设第1 支路至第g 支路之间相互均有耦合,则有

式中,所有互感电压前取“+”号或“-”号决定于各电感的同名端和电流、电压的参考方向。其次注意![]() ,…,其余支路之间由于无耦合,可以得到
,…,其余支路之间由于无耦合,可以得到
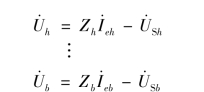
上式中的下标h=g+1,这样,支路电压与支路电流之间的关系可用下列矩阵形式表示,即
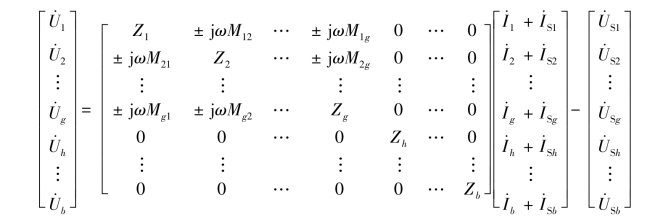
矩阵方程简写为
![]()
式中,阻抗矩阵Z 为支路阻抗矩阵,其主对角线元素为各支路阻抗,而非对角线元素将是相应的支路之间的互感阻抗,因此Z 不再是对角阵。
(3)考虑电路中含有受控源不含耦合电感的情况。如果第k 条支路中有受控电压源,它受第j 条支路中无源元件中的电流 或电压
或电压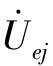 控制,且有
控制,且有![]() 或
或![]() ,式(10-21)在电流控制电压源的情况下得到(https://www.daowen.com)
,式(10-21)在电流控制电压源的情况下得到(https://www.daowen.com)
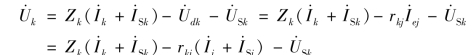
在电压控制电压源的情况下得到

从而得

式中,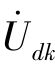 为电流控制电压源的电压时,Zkj=-rkj;
为电流控制电压源的电压时,Zkj=-rkj;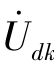 为电压控制电压源的电压时,Zkj=-μkjZj。
为电压控制电压源的电压时,Zkj=-μkjZj。
矩阵方程可简写为
![]()
式中阻抗矩阵Z 为支路阻抗矩阵,其主对角线元素为各支路阻抗,而非对角线元素将是相应的支路受控源系数,因此Z 不再是对角阵。但方程形式与式(10-23)相同。
下面推导回路电流方程的矩阵形式,重写所需3 组方程,即
KCL
![]()
KVL
![]()
支路电压方程
![]()
把支路电压方程代入KVL,可得

再把KCL 代入便得到
![]()
或为
![]()
式中,Zl≜BZBT称为回路阻抗矩阵,是一个l 阶矩阵,![]() 都为l 阶列向量。式(10-24)即为回路电流方程的矩阵形式。
都为l 阶列向量。式(10-24)即为回路电流方程的矩阵形式。
【例10-3】 电路如图10-14 所示,选支路(1,2,3,4,5)为树,试写出此电路的回路电流方程的矩阵形式。
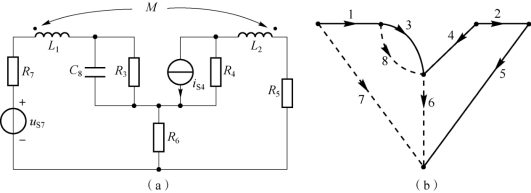
图10-14 例10-3 图
解:在图10-14(b)所示有向图中,对于所选树的单连支回路(基本回路)组为l1(6,2,4,5),l2(7,1,2,3,4,5),l3(8,3),各回路方向为该回路中的连支方向,则

故
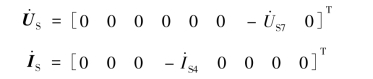
将以上各矩阵代入到式![]() 中,得到回路电流方程的矩阵形式为若选网孔为一组独立回路,则回路电流方程即为网孔电流方程。
中,得到回路电流方程的矩阵形式为若选网孔为一组独立回路,则回路电流方程即为网孔电流方程。
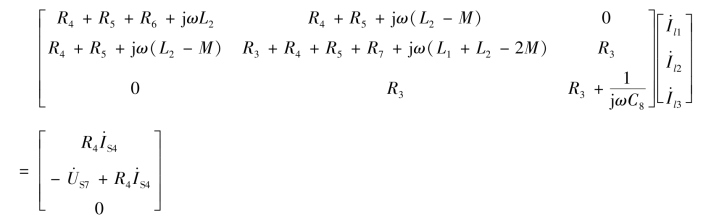
编写回路电流方程必须选择一组独立回路,一般选用基本回路组,从而可以通过选择一个合适的树处理。树的选择固然可以在计算机上按编写好的程序自动进行,但比结点电压法更烦琐。另外,由于在实际的复杂电路中,独立结点数往往少于独立回路数,故目前在计算机辅助分析的程序中,广泛采用结点法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







