有向图的拓扑性质可以用关联矩阵、回路矩阵和割集矩阵描述，本节介绍拓扑图的这3种矩阵表示，以及它们的基尔霍夫定律的矩阵形式。

1.关联矩阵

表示点与支路的关联性的矩阵称为关联矩阵，若一条支路连接某两个结点，则称该支路与这两个结点相关联。

设有向图的结点数为n，支路数为b，且所有结点与支路均加以编号，则该有向图的关联矩阵为一个n×b的矩阵，用Aa表示，它的行对应结点，列对应支路，其中的元素ajk定义如下：

ajk＝＋1，表示支路k 与结点j 关联并且支路的方向背离结点j；

ajk＝－1，表示支路k 与结点j 关联并且支路的方向指向结点j；

ajk＝0，表示支路k 与结点j 无关联。

例如，拓扑图如图10-9 所示，它的关联矩阵为

从式（10-2）中可以看出：

（1）矩阵中每一行的非0 元素表明了对应结点与哪些支路相关联；

（2）矩阵中每一列有两个非0 元素且一正一负，因为它们表示着这条支路与两个结点相关，且该支路背离一个结点而指向另一个结点；

（3）所有元素按列相加等于零，根据矩阵知识可以知道每一行的元素都可以通过其他行的元素相加得到，这个n×b 阶的矩阵Aa各行不相互独立。

如果划去Aa的任意一行，所得的（n－1）× b 阶矩阵被称为降阶关联矩阵A。例如，若将式（10-2）中的第4 行划去，得

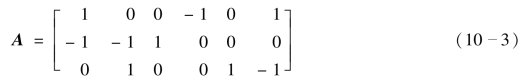
式（10-3）中，第3、4、5 列中仅有一个非零元素，这些列所对应的支路则与划去行的对应结点相关联，被划去行的对应结点可以作为参考结点。

设支路电流的参考方向就是支路的方向，电路中的b 个支路电流可以用一个b 阶列向量表示，即

如果用矩阵A 左乘电流列向量i，则乘积是一个（n－1）阶列向量，由于矩阵A的每一行对应于一个结点，且每一行中的非零元素表示与该结点相关联的支路，所以这个乘积列向量的每一元素恰好等于流出每个相应结点的各支路电流的代数和，即

根据KCL 有

故对于图10-9 有

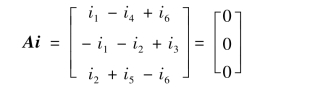
设支路电压的参考方向就是支路的方向，电路中b 个支路电压可以用一个b 阶列向量表示，即

（n－1）个结点电压可以用一个（n－1）阶列向量表示，即

由于矩阵A的每一列或矩阵AT的每一行表示每一对应支路与结点的关联情况，所以有

故对于图10-9 有

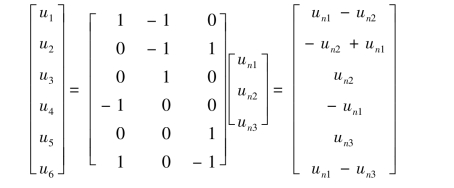
可见式（10-6）表明电路中的各支路电压可以用与该支路关联的两个结点的结点电压（参考结点的结点电压为零）表示，这正是结点电压法的基本思想，该式也可以用矩阵表示。

2.回路矩阵

表示回路与支路的关联关系的矩阵称为回路矩阵。设有向图的独立回路数为l，支路数为b，且所有独立回路和支路均要编号，则该有向图的回路矩阵是一个l×b的矩阵，用B 表示。B的行对应于回路，列对应于支路，它的任一元素bjk定义如下：

（1）bjk＝＋1，表示支路k 与回路j 关联，且它们的方向一致；

（2）bjk＝－1，表示支路k 与回路j 关联，且它们的方向相反；

（3）bjk＝0，表示支路k 与回路j 无关联。

例如，图10-9 所示的有向图，独立回路数等于3，若选网孔为独立回路，选顺时针方向为回路绕行方向，如图10-10（a）所示，则对应的回路矩阵为

如果所选独立回路组对应于一个树的单连支回路组，则这种回路矩阵就称为基本回路矩阵，用Bf表示。

Bf的行、列次序是先把l 条连支依次排列，然后再排列树支；取每一连支回路的序号为对应连支所在列的序号，且以该连支的方向为对应回路的绕行方向，Bf中将出现一个l 阶的单位子矩阵，即有

式（10-7）中下标l 和t 分别表示与连支和树支对应的部分。(www.daowen.com)

例如，在图10-10（b）所示有向图中，选支路1、4、6 为树支，则支路2、3、5 为连支，回路（2，1，6）、（3，4，1）、（5，4，6）为一组单连支回路，可以将回路矩阵写成基本回路矩阵形式，即

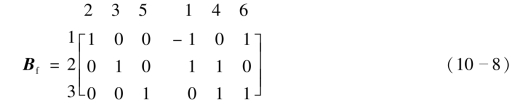
回路矩阵左乘支路电压列向量，所得乘积是一个l 阶的列向量。由于矩阵B的每一行表示每一对应回路与支路的关联情况，由矩阵的乘法规则可以知道乘积列向量中每一元素将等于每一对应回路中各支路电压的代数和，即

根据KVL 有

实际上式（10-9）是用矩阵B 表示的KVL的矩阵形式。例如，将式（10-8）代入式（10-9）中可得

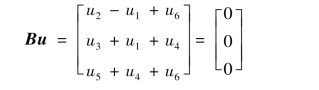
l 个独立回路电流用一个l 阶列向量表示，即

由于矩阵B的每一列或者说矩阵BT的每一行表示每一对应支路与回路的关联情况，由矩阵的乘法可以得到支路电流矩阵和回路电流矩阵的关系为

例如，对于图10-10（a）有

所以，式（10-10）表示的是电路中各支路电流用与该支路关联的回路电流表示，这也正是回路电流法的基本思想，所以说该式是用矩阵B 表示的KCL的矩阵形式。

3.割集矩阵

表示支路与割集的关联性质的矩阵被称为割集矩阵，若某些支路构成一个割集，则称这些支路与该割集关联。根据应用需要，以下我们介绍的是独立割集矩阵和基本割集矩阵。

设有向图的结点数为n，支路数为b，则该图的独立割集数为（n－1）。对每个割集编号，并指定一个割集方向：移去割集的所有支路，G 被分离为两部分后，从其中一部分指向另一部分的方向即为割集方向。则割集矩阵为一个[（n－1）×b]的矩阵，用Q 表示。Q的行对应割集，列对应支路，它的任一元素qjk定义如下：

（1）qjk＝＋1，表示支路k 与割集j 关联，且它们的方向一致；

（2）qjk＝－1，表示支路k 与割集j 关联，且它们的方向相反；

（3）qjk＝0，表示支路k 与割集j 无关联。

例如，拓扑图如图10-11 所示。

结点数为4，独立割集数等于3，若选一组独立割集如图所示，对应的割集矩阵为

若选取的割集是一组单树支割集，则此割集矩阵称为基本割集矩阵，用Qf表示。写Qf时其行、列的次序为：先将（n－1）条树支依次排列，然后依次排列连支，且选割集方向与相应树支方向一致，则Qf为

式（10-11）中，下标t 和l 分别表示对应与树支和连支部分。例如，图10-11 中，选支路1、4、6 为树支，支路2、3、5 为连支，可得基本割集矩阵为

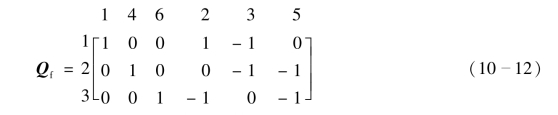
在割集中，属于一个割集所有支路电流的代数和等于零，根据割集矩阵的定义和矩阵的乘法可以得出

式（10-13）是用割集矩阵Q 表示的KCL的矩阵形式。例如，在图10-11 所示有向图中，所选的割集是一组基本割集，也是独立割集，将式（10-12）代入式（10-13）中有

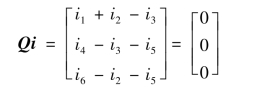
电路中（n－1）个树支电压可以用一个（n－1）阶列向量表示，即

由于通常选单树支割集为独立割集，此时树支电压又可视为对应的割集电压，所以ut又是基本割集组的割集电压列向量。由于矩阵Qf的每一列，即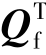的每一行，表示一条支路与割集的关联情况，根据矩阵相乘的规则可求得

式（10-14）是用矩阵Qf表示的KVL的矩阵形式。例如，图10-11 所示的有向图及其所选的割集，支路1、4、6 为树支，支路2、3、5 为连支，Qf如式（10-12），则有

即

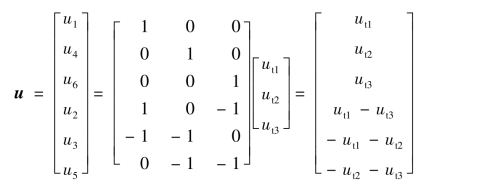
式（10-14）表明电路中的支路电压可以用树支电压（割集电压）表示，这就是割集电压法的基本思想。

A、Bf和Qf的KCL 和KVL的矩阵形式如表10-1 所示。

表10-1　KCL 和KVL的矩阵形式