本节通过图论的初步知识，主要介绍了如何应用网络拓扑图表示电路的连接性质。

1.图的定义

图论是拓扑学的一个分支，富有趣味性，是应用极为广泛的一门学科，将图论应用于电路网络分析称为网络图论。在电路分析中，若把电路中的每一条支路都画成抽象的线段，形成结点和支路的集合，则每条支路的两端都连到相应的结点上。支路用线段描述，结点用点描述，这种从电路抽象出来的几何图形称为电路的图，简称图，所以说图是支路和结点的集合，表示为

支路和结点的定义如下。

（1）支路：若干元件无分岔地首尾相连构成支路，即若干元件的串联和并联都作为一条支路；

（2）结点：3 个或3 个以上支路的连接点称为结点。

例如，图10-1（a）为一个具有6 个电阻和2 个独立电源的电路，根据以上定义可以画出相应的电路图，其中图10-1（b）、（c）分别是无向图和有向图。无向图是指未赋予支路方向的图，而有向图是指赋予支路方向的图，电流、电压取关联参考方向。在电路中通常指定每一条支路中的电流参考方向，电压一般取关联参考方向。电路的图的每一条支路也可以指定一个方向，此方向即该支路电流（和电压）的参考方向。

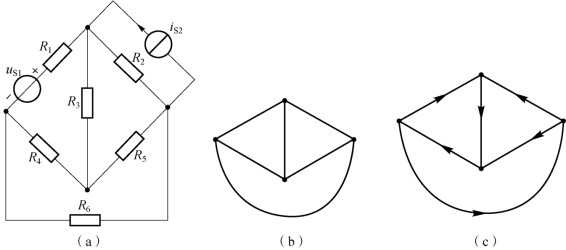
图10-1　电路的图

（a）电路图；（b）无向图；（c）有向图

注意：

在图的定义中，结点和支路各自为一个整体，但任意一条支路必须终止在结点上。移去一条支路并不等于同时把它连接的结点也移去，所以允许有孤立结点存在，它表示一个与外界不发生联系的“事物”。若移去一个结点，则应当把与该结点连接的全部支路都移去。

2.路径

从一个图G的某一结点出发沿着一些支路连续移动到达另一结点（或回到原出发点），这样所经过的一系列支路构成图G的一条路径。一条支路本身也算为路径。当图G的任意两个结点之间至少存在一条路径时，图G 称为连通图，非连通图至少存在两个分离部分，如图10-1（c）就是连通图。

3.子图

若图G1 中所有支路和结点都是图G 中的支路和结点，则称G1 是G的子图，图10-2（b）、（c）、（d）是（a）的子图。

连通图G的树T 定义：包含图G的全部结点且不包含任何回路的连通子图，即树T 是连通图G的一个子图，满足的条件是连通的，包含所有结点，但不包含闭合路径。图10-2（b）是树，图10-2（c）、（d）就不是树，因为（c）有一个结点没有包括，（d）图是一个闭合路径。

树中包含的支路称为树支，而其他支路则称为连支。对于图10-3（a）所示的图G，取支路（1，4，6）为树，如图10-3（b）中实线表示，相应的连支为（2，3，5），如图10-3（b）中虚线表示。

说明：

对于一个具有b 条支路，n 个结点的图G，有很多树，但树支的数目是n－1。连支的数目为b－（n－1）。

4.回路与回路独立方程

回路是连通图的一个子图，构成一条闭合路径，满足条件：（1）连通；（2）每个结点关联2 条支路。如图10-3（a）中，支路（1，3，4）、（2，5，3）、（4，5，6）等都构成了回路。

由于连通图G的树支连接所有结点又不形成回路，因此，对于图G的任意一个树，加入一个连支后，就会形成一个回路，并且此回路除所加连支外均由树支组成，这种回路称为单连支回路或基本回路。对于图10-4（a）所示图G，取支路（5，6，7，8）为树，在图10-4（b）中用实线表示，相应的连支为（1，2，3，4），对应于这一树的基本回路是（6.5，1）、（6，7，2）、（7，8，3）、（5，8，4），每一个基本回路仅含一个连支，且这一连支并不出现在其他基本回路中，基本回路的个数显然等于连支数。如果对基本回路列写KVL 方程，由于每个连支只在一个回路中出现，因此这些KVL 方程必构成独立方程组，所以根据基本回路所列出的KVL 方程组是独立方程。对于图10-4（b）的基本回路恰好也是第2 章所说的网孔。但是一个图G的树不是唯一的，当然基本回路也不是唯一的，选择不同的树，就可以得到不同的基本回路。如图10-4（c）中，取支路（2，6，8，4）为树，相应的连支为（1，5，7，3），对应于这一树的基本回路是（2，6，7）、（6，8，4，1）、（4，8，5）、（2，6，8，3）。可见，对一个具有b 条支路和n 个结点的电路，连支数l＝b－n＋1，这也是一个图的独立回路的数目。(www.daowen.com)

【例10-1】　给定直流电路如图10-5（a）所示，试选择一组独立回路，列出支路电流方程和回路电流方程。

解：电路拓扑图如图10-5（b）所示，选取支路（4，5，6）为树，3 个基本回路绘在图中，以图中回路绕行方向列出KVL 方程

各支路电流和电压的关系为

将以上公式代入式（10-1），得到支路电流方程，即

图10-5（b）中绘出回路电流Il1、Il2、Il3及其绕行方向，连支电流I1、I2、I3即为回路电流Il1、Il2、Il3。以回路电流为变量列出基本回路的KVL 方程为

5.割集

结点电压法是通过观察法列出的，但对于规模较大的电路应用计算机辅助分析需要应用网络图论，本节介绍与结点电压有关的割集概念。

连通图G的一个割集Q 是G的一个支路集合，具有性质：（1）把Q 中全部支路移去，图分成两个分离部分；（2）任意放回Q 中一条支路，仍构成连通图。

注意：

这里的支路移去是仅仅移去支路而保留其相关的结点。如图10-6（a）所示，移去支路5、6、7、8，与这4 条支路相关的结点均保留，特别是结点⑤，虽然相关的支路移走，该结点成为孤立结点，但必须保留在图中，由此得到的子图G1为图10-6（b）所示。

一般情况下，对于一个连通图，可看作一个闭合面，被该闭合面切割的所有支路全部移去，则原连通图会被分割成两个部分，则这样的一组支路的集合就称为原连通图的割集。例如，图10-7（a）中的割集有Q1（1，2，4），Q2（2，5，3），Q3（1，3，6），Q4（4，5，6），其中割集包围的是一个结点。而在图10-7（b）中，割集Q1（6，3，7）包围的是一个广义结点。Q2（6，3，7，5，9）不能称为割集，因为移去这些支路将连通图分割成3 个部分，（6，3，7，5）也不能是割集，因为加入支路5 仍然不是连通的。

借助于“树”确定一组独立割集的方法如下。

对于一个连通图，如任选一个树，则与树对应的连支集合不能构成一个割集，而它的每一个树支与一些相应的连支都可以构成一个割集。

基本割集即为单树支割集，由树的一条树支与相应的一些连支构成的割集，对于一个具有n 个结点和b 条支路的连通图，其树支数为（n－1），因此将有（n－1）个基本割集。

例如，在图10-8 中，结点有6 个，支路有9 条，选择支路（1，2，3，4，5）为树支，在图中以实线表示，其余支路为连支，在图中以虚线表示，则基本割集组为Q1（1，8，6）、Q2（2，7，8）、Q3（3，6，7）、Q4（4，9，6）、Q5（5，7，9）。

注意：

①连支集合不能构成割集；

②属于同一割集的所有支路的电流应满足KCL，如果一个割集的所有支路都连接在同一个结点上，则割集的KCL 方程变为结点上的KCL 方程；

③对应一组线性独立的KCL 方程的割集称为独立割集，基本割集是独立割集，但独立割集不一定是单树支割集。