对于正弦电路，完全响应包括两部分，一部分是与电路输入形式相同的稳态响应，另一部分是随时间衰减为零的暂态响应。如果将电源模型化为一个50 Hz的正弦波，则稳态响应也是同频率的正弦波，其幅度和相位可以用相量法计算出来。暂态响应和电路元件性质、元件值、连接方式有关，如果电源连接到电路中，则电路中每个元件上电压和电流都是由暂态部分和稳态部分组成。

尽管暂态电压或者电流最终会衰减到零，但是在一开始叠加到稳态分量上的时候，总的电压或电流可能会超过元器件的额定值，这就是为什么要确定电路完全响应的重要原因，应用本章介绍的拉普拉斯变换技术能用来确定电路对正弦电源的完全响应。

【例9-34】　电路如图9-26（a）所示，已知R＝200 Ω，C＝1 μF，L＝0.25 H，uS（t）＝100cos 314t V 为正弦电源。原来电路没有储能，当t＝0 时开关S 闭合。求电流i（t）。

解：将图9-26（a）时域电路图转换为运算电路，如图9-26（b）所示。因为原来的电路没有初始储能，故此电路中无内电源。电压源象函数为

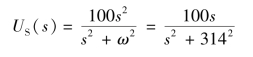
整个电路的运算阻抗为

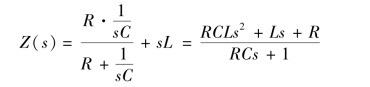
故电流的象函数为

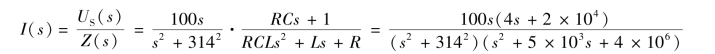
分母特征方程的4 个根为

将I（s）展开成部分分式，有

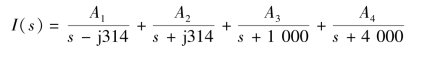
分别求各分式系数

s1和s2是一对共轭复数，A1和A2也是一对共轭复数，所以

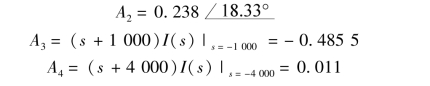
故时域函数为

当t＝0 时，i（0）为

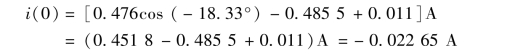(www.daowen.com)

暂态分量的最大值为0.485 5，比稳态分量的最大值还要大，在本题中可以恰好与稳态分量相抵消，不会造成电路过电流，但有的电路则会出现。

【例9-35】　电路如图9-27（a）所示，已知R＝15 Ω，C＝100 μF，L＝0.01 H，uS（t）＝cos（314t）V 为正弦电源。原来的电路没有储能，当t＝0 时开关S 闭合，求电流i（t）。

解：将图9-27（a）时域电路转换为运算电路，如图9-27（b）所示。电路的运算电阻为

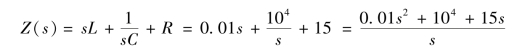
电流的象函数为

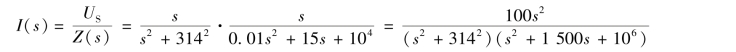
部分分式展开式为

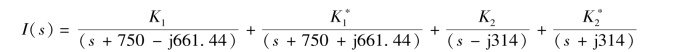
确定各分式系数为

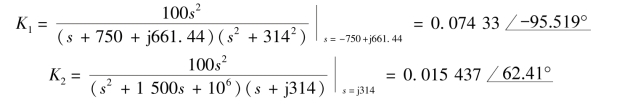
故时域函数为

第一部分为暂态响应，经过7 ms 后会衰减到零。第二部分为稳态响应，只要电源连接好，则该响应一定存在。

当t＝0 时，i（0）为

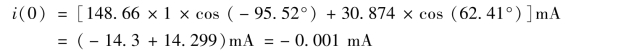
此时，暂态分量较大，恰好与稳态分量抵消，电路中电流很小。

当t＝1 ms 时，i（0.001）为

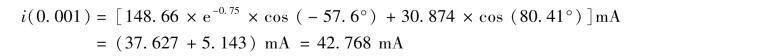
此时，第一部分的暂态分量为37.627，为稳态分量最大值的1.22 倍，很可能会超过器件的额定值。

该例表明：对于正弦输入电源，尽管稳态响应能够满足要求，但是暂态响应也不可忽视。