分析连续时间系统的响应、稳定性、频率响应，拉氏变换起着桥梁的作用，它将系统的时域微分方程变换为复频域中的代数方程，简化了计算。但是，由于复频域s 并非一个具体的数值，对于高阶系统，手工分析的话计算量还是比较大，因此要借助MATLAB 计算机辅助分析。

1.辅助分析拉氏变换

信号F（t）的单边拉氏变换定义为

拉氏变换在MATLAB 中对应的指令为

其中，t 为积分变量t；s 为复频率s；L 为f（t）的拉氏变换F（s）。如果f（t）中t 为MATLAB规定的积分变量，而且用s 表示复频率，指令可简写成

【例9-28】　用MATLAB 求f1（t）＝sin（2t）ε（t）和f2（t）＝e－atε（t）的拉氏变换。

解：求f1（t）和f2（t）拉氏变换的M 文件如下：

输出结果：

【例9-29】　求冲激函数δ（t）和阶跃函数ε（t－a）的拉氏变换，其中a>0。

解：冲激函数δ（t）和阶跃函数ε（t）在符号分析程序Maple 中分别用Dirac（t）和Heaviside（t）表示，高阶冲激函数δ（n）（t）用Dirac（n，t）表示，由于MATLAB 本身对冲激函数和阶跃函数没有定义，因此，必须将它们定义为符号对象。

冲激函数和阶跃函数拉氏变换的M 文件如下：

ds 输出结果：

es 输出结果：

2.辅助分析拉氏反变换

拉氏反变换的定义式为

实现上式运算的指令格式为

或简写为

【例9-30】　求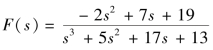的反拉氏变换。

解：由于F（s）为有理分式，可先将分子、分母多项式的有关系数用数组表示，再利用poly2sym 函数将其转换为多项式，其M 文件如下：

输出结果：

根据分式多项式，即

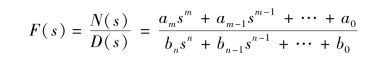
如果所有极点互不相等，则F（s）可展开为

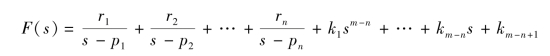
在MATLAB 中对上式进行部分分式展开的指令为

其中，a 是由F（s）分子多项式系数组成的行向量a，a＝[am，am－1，…，a1，a0]，b 是由F（s）分母多项式系数组成的行向量b，b＝[bn，bn－1，…，b1，b0]，返回值r 是留数列向量r，r＝[r1，r2，…，rn]T；p 是极点列向量p，p＝[p1，p2，…，pn]T；k 是直接项系数行向量k。

【例9-31】　用MATLAB 辅助求解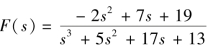的拉氏反变换。

解：使用residue 函数求解，M 文件如下：

(www.daowen.com)

输出结果：

F（s）的展开式为

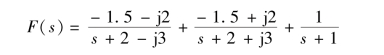
于是

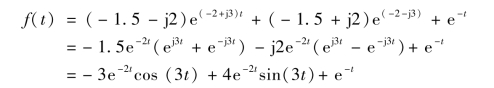
函数residue 也可将部分分式转换为两个多项式之比形式，其格式为

对上例中的部分分式进行转换，M 文件如下：

输出结果：

【例9-32】　应用MATLAB 辅助求解的原函数f（t）。

解：F（s）的分母多项式在p1＝－1 处具有三重根，p2＝0 处有二重根，用根构造多项式的指令为

其中，r 为多项式的根向量。其M 文件如下：

分母多项式系数输出结果：

留数与极点输出结果：

则

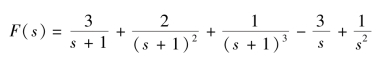
相应的原函数为

3.辅助分析网络函数频率特性

系统传递函数描述为

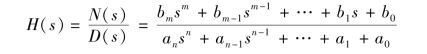
MATLAB 中构造描述分子和分母多项式的行向量为

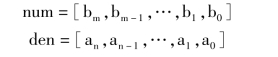
MATLAB 中提供了一种sys 对象，用于描述系统对象的创建，其构造语句为

MATLAB 也提供了根据系统对象sys 直接绘制系统的波特图来分析系统的频率特性，其函数为

【例9-33】　应用MATLAB 辅助分析RC 低通滤波器的频率特性，电路如图9-24 所示。

解：输入到输出的网络传递函数为

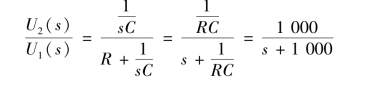
其M 文件如下：

MATLAB 仿真的幅频特性和相频特性如图9-25 所示。

由仿真结果可知，测量指针测出的截止频率为

其大小与理论计算完全相同。