如果用相量法求例9-26的电路在正弦稳态下的网络函数，网络函数中的将分别是jωL、，输入电压US（s）和输出电压UC（s）将是相量U·S和U·C，这样网络函数H（jω）为

可见，将H（s）中的s 用jω 替换，则。也就是说，在s＝jω 处计算所得网络函数H（s）即为H（jω），而H（jω）是角频率为ω 时正弦，稳态情况下的输出相量与输入相量之比。

对于某一固定角频率ω，H（jω）通常是一个复数，即

式中｜H（jω）｜为网络函数在频率ω 处的模值，称为幅频特性；φ＝arg[H（jω）]随频率ω 变化的关系称为相位频率响应，简称相频特性，幅频特性和相频特性统称为频率响应。

以下讨论网络函数的零点、极点对网络频率响应的影响。

网络函数的解析式又可写为

令s＝jω，则得到正弦稳态下的网络函数有

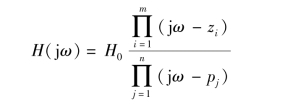
于是幅频特性为

(www.daowen.com)

相频特性为

所以，若已知网络函数的极点和零点，则按式（942）和式（9-43）便可以计算对应的频率响应。

【例9-27】　图9-22 为RC 串联电路，试定性分析以电压u2为输出时网络的频率响应。

解：以uC为电路变量输出的网络函数为

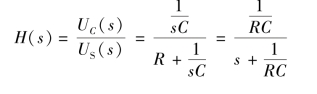
令M＝｜jω－p1｜，，则

RC 串联电路的频率响应如图9-23 所示。

H（jω）在ω＝ω1、ω2和ω3时的模值为H0除以图9-23（a）中的线段长度M1、M2和M3，对应的相位分别为图中的θ1、θ2和θ3的负值。当ω→∞时，｜H（jω）｜→0，相位从零趋近于－90°。

可以看出，该电路网络具有低通特性。

当ω＝0 时，H（jω）＝1∠0°；当时，，相当于ω＝0 时模值的0.707，此频率称为低通滤波电路的截止频率，用ωc表示，频段0 到ωc的频率范围称为通频带。