根据网络函数的定义可知，电路的零状态响应的象函数为

式中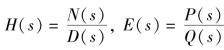，，而N（s）、D（s）、P（s）、Q（s）都是s的多项式。用部分分式法求响应的原函数时，D（s）Q（s）＝0的根将包含D（s）＝0 和Q（s）＝0的根。响应中包含Q（s）＝0的根的那些项属于时域分析中的强制分量，而包含D（s）＝0的根（即网络函数的极点）的那些项则是自由分量或瞬态分量。

一般情况下h（t）的特性就是时域响应中自由分量的特性，而h（t）＝L－1[H（s）]，因此，分析网络函数的极点位置与冲激响应的关系可以分析网络的稳定性。

1.极点全部位于s 平面的左半平面

设网络函数H（s）为真分式且具有单阶极点，则单位冲激响应为

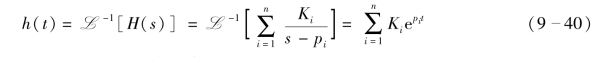
式中，Ki为常数，pi（i＝1，2，…，n）为极点。

从式（9-40）可以看出，零点在s 平面上的位置只影响Ki的大小，极点在s 平面上所处位置影响单位冲激响应h（t）的变化规律。

当pi为负实数时，设，则极点p＝－a，h（t）＝e－at，h（t）按衰减的指数规律变化，当t→∞时，单位冲激响应将趋于零，这时称对应的网络是非振荡渐近稳定的，其波形及极点在s 平面上的位置如图9-20 所示。

当极点为共轭复数时，设，则极点p1＝－a＋jω，p2＝－a－jω，h（t）＝e－atsin ωt，当t→∞时，单位冲激响应也将趋于零，这时称对应的网络是振荡渐近稳定的，其波形及极点在s 平面上的位置如图9-20 所示。

前面假设的网络极点是单阶极点，实际上，当网络函数H（s）的极点全部位于s的左半平面时，单位冲激响应均是有界的。例如，设，极点p1＝p2＝－a<0 为二阶极点，，称网络是渐近稳定的。

2.极点位于s 平面的右半开平面(www.daowen.com)

假设网络函数为真分式且具有单阶极点，但至少有一个极点位于s 平面的右半平面，当极点位于右半平面时，设，极点p＝a >0，h（t）＝eat，当t→∞时，h（t）→∞，所以电路网络不稳定。若设，则极点p1，2＝a±jω，Re[p1]＝Re[p2]＝a>0，h（t）＝eatsin ω t，网络函数的单位冲激响应波形都是随时间增长且无界的，称网络是不稳定，其波形如图9-20 所示。

3.极点位于虚轴上

虚轴上存在共轭单阶极点。例如，，极点p1，2＝±jω，h（t）＝Asin（ωt），网络函数的单位冲激响应是等幅正弦波，其波形如图9-20 所示。

4.极点为零

当网络函数的极点为零，即p＝0 时，网络函数为，网络函数的单位冲激响应为h（t）＝ε（t），其波形是单位阶跃函数，这时也称网络是不稳定的。

【例9-26】　RLC 串联电路接通恒定电压源US，如图9-21（a）所示，根据网络函数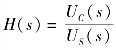的极点分布情况分析uC（t）的变化规律。

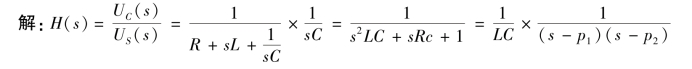
讨论：

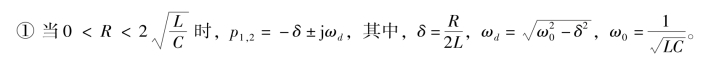
这时网络函数H（s）的极点位于s 左半平面，如图9-21（b）中的p1、p2，根据图9-20 可知，uC（t）的自由分量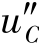（t）为衰减的正弦振荡，其包络线为e－δt，振荡角频率为ωd，而且极点离开虚轴越远，振荡衰减越快。

②当R＝0 时，δ＝0，ωd＝ω0，故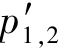＝±jω0，H（s）的极点位于虚轴上，因此，uC（t）的自由分量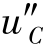（t）为等幅振荡且ωd的绝对值越大，等幅振荡的振荡频率越高。

③当，H（s），的极点位于负实轴上，因此，uC（t）的自由分量u″C（t）由两个衰减速度不同的指数函数组成，且极点离原点越远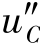，（t）衰减越快。uC（t）的强制分量u′C（t）取决于激励US。