根据网络函数的定义,零状态响应为R(s)=H(s)E(s),当E(s)=1 时,R(s)=H(s),即网络函数就是该响应的象函数,而当E(s)=1 时,e(t)=δ(t),所以网络函数的原函数h(t)是电路的单位冲激响应,即
![]()
当E(s)为任意外部激励e(t)的象函数,H(s)为网络的冲激响应h(t)的象函数,则R(s)为外施任意激励函数的零状态响应。所以,在时域中,如果求任意外施激励的零状态响应r(t),则需要求出单位冲激函数激励下的网络函数H(s),再求出任意外施激励e(t)的象函数E(s),根据R(s)=H(s)E(s)求出R(s),最后将R(s)拉氏反变换,求出r(t)。
根据定义式,求R(s)的拉氏反变换,得到时域中的响应为
![]()
式(9-38)中右端是卷积积分,卷积是电路分析的一个重要概念,在时域中可以求出任意激励函数的零状态响应,该式也符合卷积定理,这样,在复频域求解降低了在时域中求卷积的难度。
【例9-21】 图9-16(a)中电路激励为iS(t)=δ(t),求冲激响应h(t),即电容电压uC(t)。
解:图9-16(b)为运算电路,由于此冲激响应为电路端电压,与冲激电流源激励属于同一端口,因而网络函数为驱动点阻抗,即
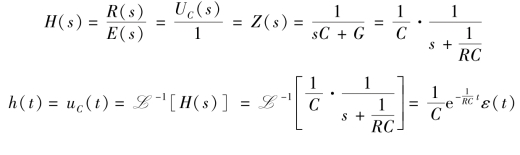
【例9-22】 电路如图9-17(a)所示,先求其冲激响应iL(t),再由冲激响应求网络函数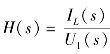 。
。
解:运算电路如图9-17(b)所示,先求其冲激响应iL(t)。
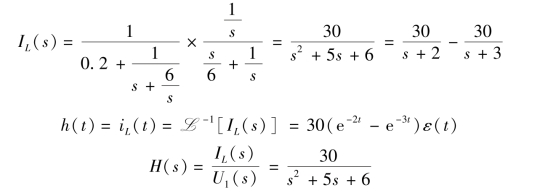
【例9-23】 已知描述某线性时不变(LTI)单输入—单输出网络的微分方程式为
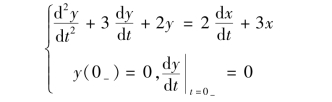
式中,y 为零状态响应;x 为输入激励。试求该电路网络的网络函数H(s)和单位冲激响应h(t)。
解:先对微分方程两边取拉氏变换,有(https://www.daowen.com)
![]()
即
![]()
则网络函数为
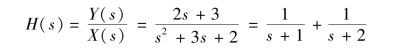
单位冲激响应为
![]()
【例9-24】 图9-18 所示为RC 并联电路,其中R=100 kΩ,C=1 μF,电容的初始状态为零,电流源的电流iS(t)=2e-tμA。求uC(t)。
解:方法一:应用网络函数求解。
由例9-21 可知网络函数为
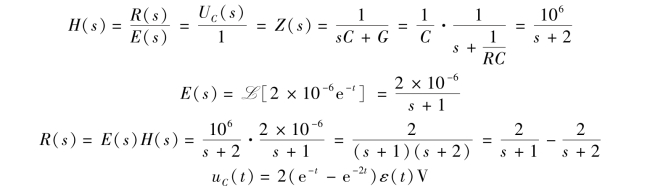
方法二:应用卷积积分。
由例9-21 可知,电路的冲激响应为
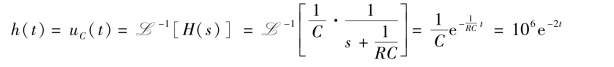
应用卷积积分式(9-38)有
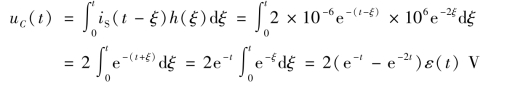
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







